Discrete-Time Distribution Steering using Monte Carlo Tree Search

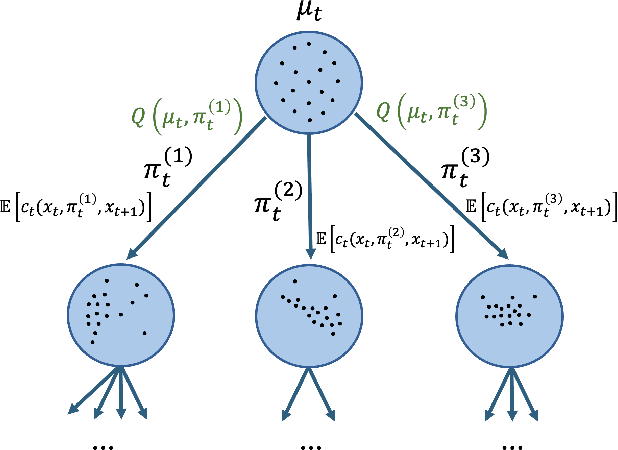
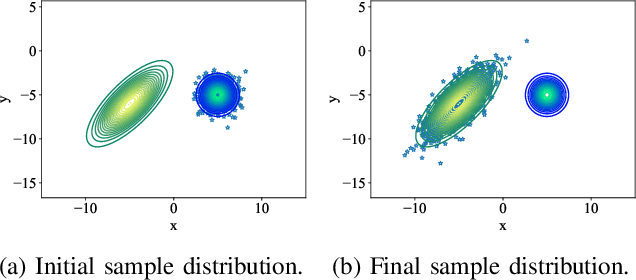
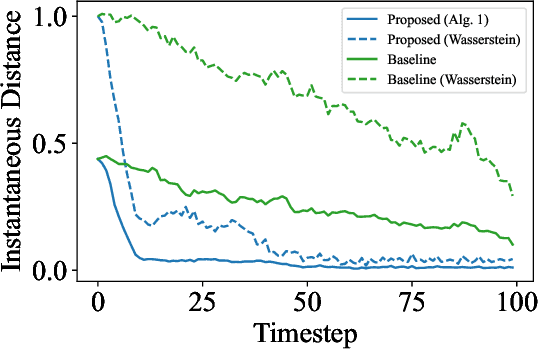
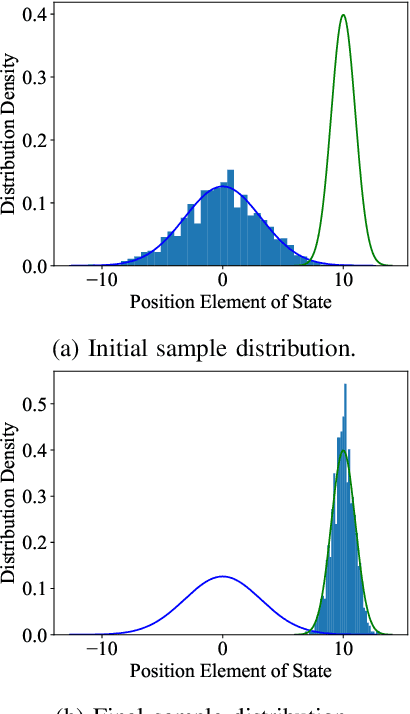
Optimal control problems with state distribution constraints have attracted interest for their expressivity, but solutions rely on linear approximations. We approach the problem of driving the state of a dynamical system in distribution from a sequential decision-making perspective. We formulate the optimal control problem as an appropriate Markov decision process (MDP), where the actions correspond to the state-feedback control policies. We then solve the MDP using Monte Carlo tree search (MCTS). This renders our method suitable for any dynamics model. A key component of our approach is a novel, easy to compute, distance metric in the distribution space that allows our algorithm to guide the distribution of the state. We experimentally test our algorithm under both linear and nonlinear dynamics.

Large-Scale GNSS Spreading Code Optimization

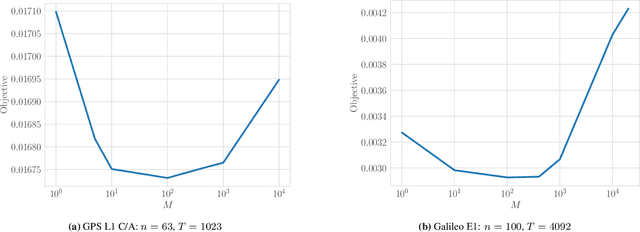
We propose a bit-flip descent method for optimizing binary spreading codes with large family sizes and long lengths, addressing the challenges of large-scale code design in GNSS and emerging PNT applications. The method iteratively flips code bits to improve the codes' auto- and cross-correlation properties. In our proposed method, bits are selected by sampling a small set of candidate bits and choosing the one that offers the best improvement in performance. The method leverages the fact that incremental impact of a bit flip on the auto- and cross-correlation may be efficiently computed without recalculating the entire function. We apply this method to two code design problems modeled after the GPS L1 C/A and Galileo E1 codes, demonstrating rapid convergence to low-correlation codes. The proposed approach offers a powerful tool for developing spreading codes that meet the demanding requirements of modern and future satellite navigation systems.

Fitting Multilevel Factor Models

We examine a special case of the multilevel factor model, with covariance given by multilevel low rank (MLR) matrix~\cite{parshakova2023factor}. We develop a novel, fast implementation of the expectation-maximization (EM) algorithm, tailored for multilevel factor models, to maximize the likelihood of the observed data. This method accommodates any hierarchical structure and maintains linear time and storage complexities per iteration. This is achieved through a new efficient technique for computing the inverse of the positive definite MLR matrix. We show that the inverse of an invertible PSD MLR matrix is also an MLR matrix with the same sparsity in factors, and we use the recursive Sherman-Morrison-Woodbury matrix identity to obtain the factors of the inverse. Additionally, we present an algorithm that computes the Cholesky factorization of an expanded matrix with linear time and space complexities, yielding the covariance matrix as its Schur complement. This paper is accompanied by an open-source package that implements the proposed methods.

Compact Model Parameter Extraction via Derivative-Free Optimization

In this paper, we address the problem of compact model parameter extraction to simultaneously extract tens of parameters via derivative-free optimization. Traditionally, parameter extraction is performed manually by dividing the complete set of parameters into smaller subsets, each targeting different operational regions of the device, a process that can take several days or even weeks. Our approach streamlines this process by employing derivative-free optimization to identify a good parameter set that best fits the compact model without performing an exhaustive number of simulations. We further enhance the optimization process to address critical issues in device modeling by carefully choosing a loss function that evaluates model performance consistently across varying magnitudes by focusing on relative errors (as opposed to absolute errors), prioritizing accuracy in key operational regions of the device above a certain threshold, and reducing sensitivity to outliers. Furthermore, we utilize the concept of train-test split to assess the model fit and avoid overfitting. This is done by fitting 80% of the data and testing the model efficacy with the remaining 20%. We demonstrate the effectiveness of our methodology by successfully modeling two semiconductor devices: a diamond Schottky diode and a GaN-on-SiC HEMT, with the latter involving the ASM-HEMT DC model, which requires simultaneously extracting 35 model parameters to fit the model to the measured data. These examples demonstrate the effectiveness of our approach and showcase the practical benefits of derivative-free optimization in device modeling.

Exponentially Weighted Moving Models

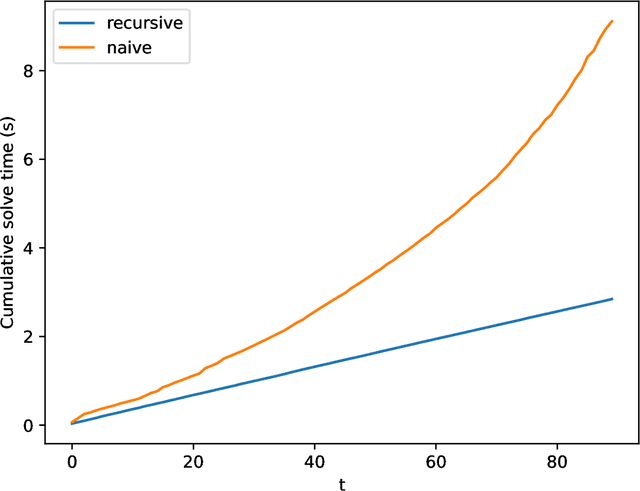
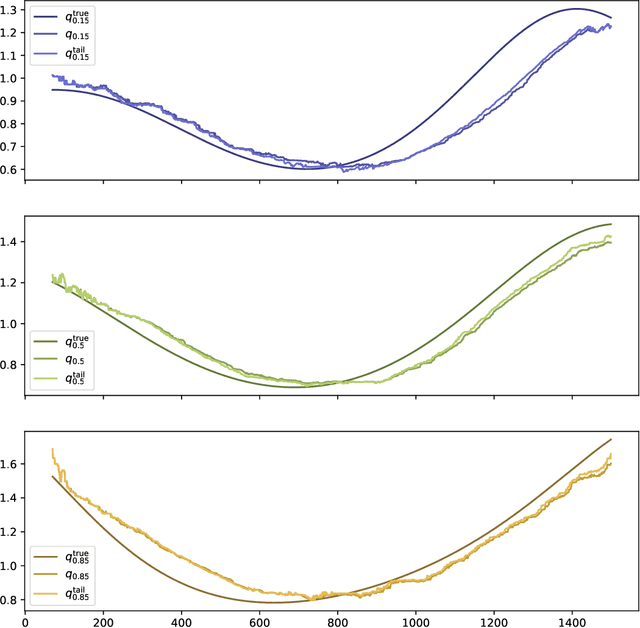
An exponentially weighted moving model (EWMM) for a vector time series fits a new data model each time period, based on an exponentially fading loss function on past observed data. The well known and widely used exponentially weighted moving average (EWMA) is a special case that estimates the mean using a square loss function. For quadratic loss functions EWMMs can be fit using a simple recursion that updates the parameters of a quadratic function. For other loss functions, the entire past history must be stored, and the fitting problem grows in size as time increases. We propose a general method for computing an approximation of EWMM, which requires storing only a window of a fixed number of past samples, and uses an additional quadratic term to approximate the loss associated with the data before the window. This approximate EWMM relies on convex optimization, and solves problems that do not grow with time. We compare the estimates produced by our approximation with the estimates from the exact EWMM method.

Approximate Sequential Optimization for Informative Path Planning

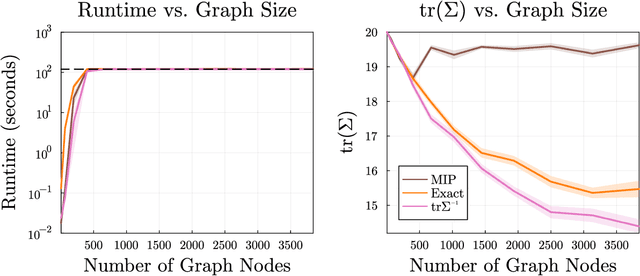
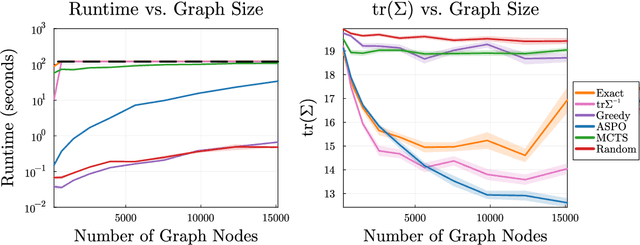
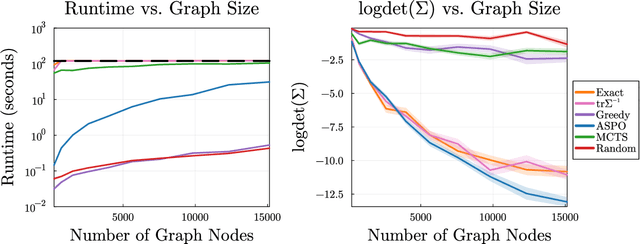
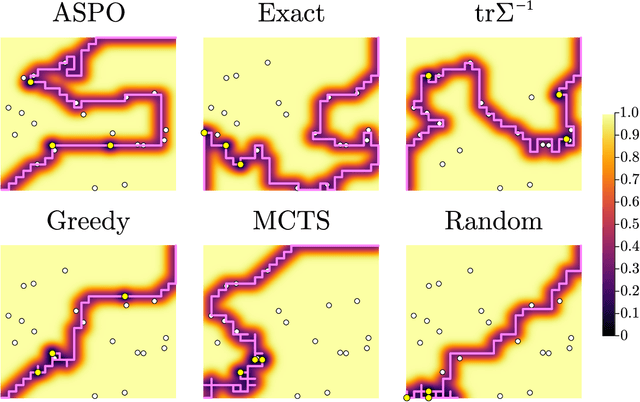
We consider the problem of finding an informative path through a graph, given initial and terminal nodes and a given maximum path length. We assume that a linear noise corrupted measurement is taken at each node of an underlying unknown vector that we wish to estimate. The informativeness is measured by the reduction in uncertainty in our estimate, evaluated using several metrics. We present a convex relaxation for this informative path planning problem, which we can readily solve to obtain a bound on the possible performance. We develop an approximate sequential method where the path is constructed segment by segment through dynamic programming. This involves solving an orienteering problem, with the node reward acting as a surrogate for informativeness, taking the first step, and then repeating the process. The method scales to very large problem instances and achieves performance not too far from the bound produced by the convex relaxation. We also demonstrate our method's ability to handle adaptive objectives, multimodal sensing, and multi-agent variations of the informative path planning problem.

Finding Moving-Band Statistical Arbitrages via Convex-Concave Optimization

We propose a new method for finding statistical arbitrages that can contain more assets than just the traditional pair. We formulate the problem as seeking a portfolio with the highest volatility, subject to its price remaining in a band and a leverage limit. This optimization problem is not convex, but can be approximately solved using the convex-concave procedure, a specific sequential convex programming method. We show how the method generalizes to finding moving-band statistical arbitrages, where the price band midpoint varies over time.

Factor Fitting, Rank Allocation, and Partitioning in Multilevel Low Rank Matrices

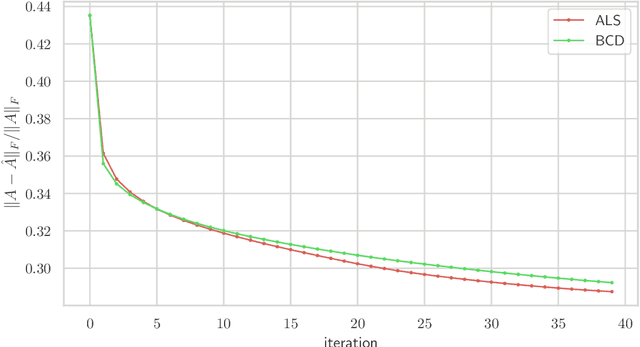
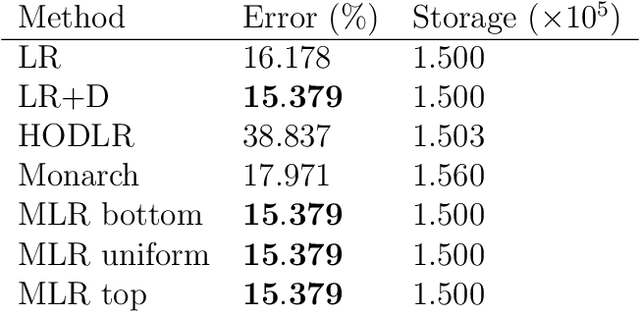
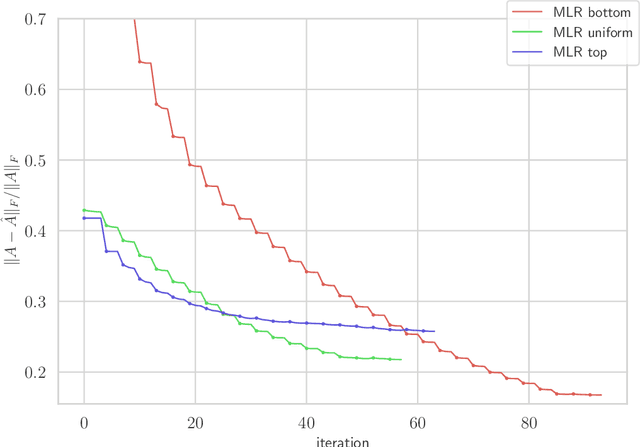
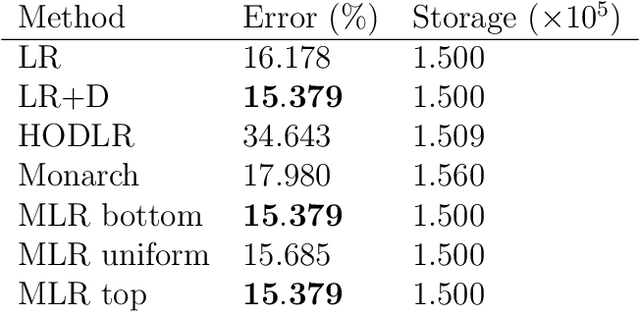
We consider multilevel low rank (MLR) matrices, defined as a row and column permutation of a sum of matrices, each one a block diagonal refinement of the previous one, with all blocks low rank given in factored form. MLR matrices extend low rank matrices but share many of their properties, such as the total storage required and complexity of matrix-vector multiplication. We address three problems that arise in fitting a given matrix by an MLR matrix in the Frobenius norm. The first problem is factor fitting, where we adjust the factors of the MLR matrix. The second is rank allocation, where we choose the ranks of the blocks in each level, subject to the total rank having a given value, which preserves the total storage needed for the MLR matrix. The final problem is to choose the hierarchical partition of rows and columns, along with the ranks and factors. This paper is accompanied by an open source package that implements the proposed methods.

Specifying and Solving Robust Empirical Risk Minimization Problems Using CVXPY

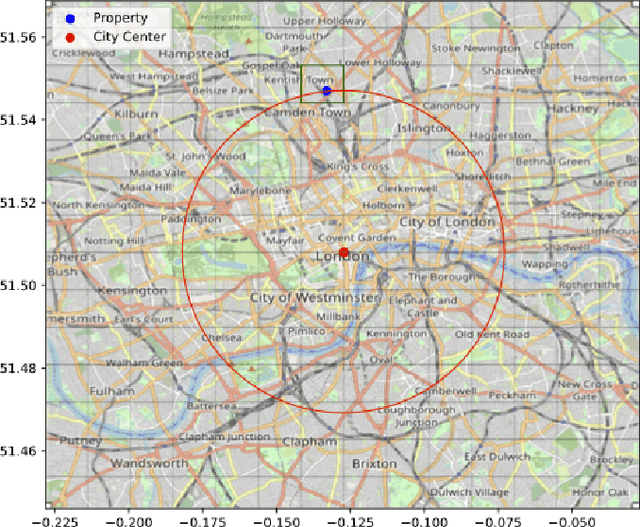
We consider robust empirical risk minimization (ERM), where model parameters are chosen to minimize the worst-case empirical loss when each data point varies over a given convex uncertainty set. In some simple cases, such problems can be expressed in an analytical form. In general the problem can be made tractable via dualization, which turns a min-max problem into a min-min problem. Dualization requires expertise and is tedious and error-prone. We demonstrate how CVXPY can be used to automate this dualization procedure in a user-friendly manner. Our framework allows practitioners to specify and solve robust ERM problems with a general class of convex losses, capturing many standard regression and classification problems. Users can easily specify any complex uncertainty set that is representable via disciplined convex programming (DCP) constraints.

Joint Graph Learning and Model Fitting in Laplacian Regularized Stratified Models

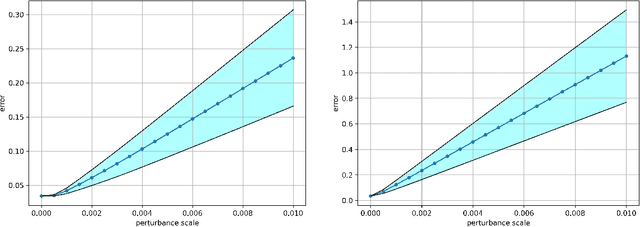
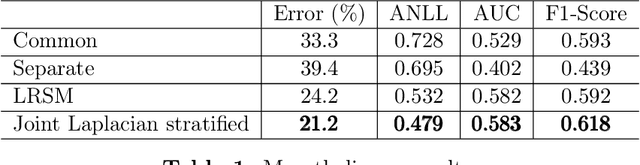
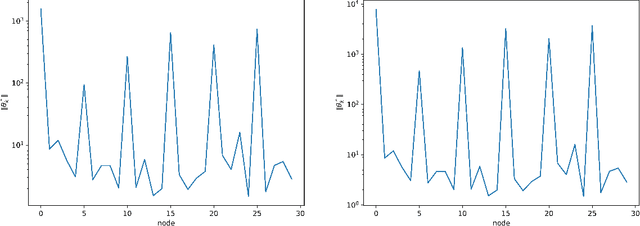
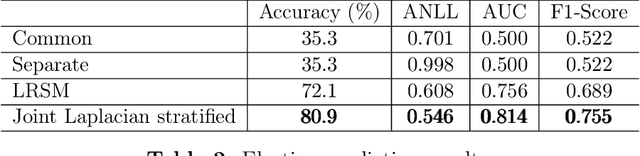
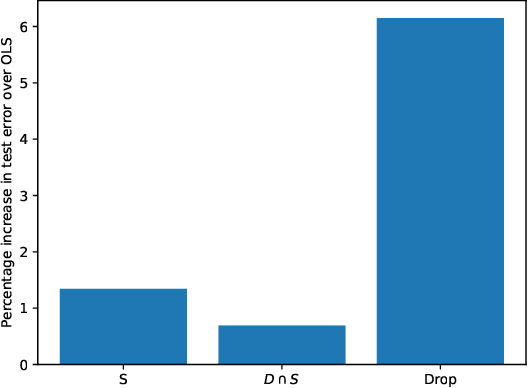
Laplacian regularized stratified models (LRSM) are models that utilize the explicit or implicit network structure of the sub-problems as defined by the categorical features called strata (e.g., age, region, time, forecast horizon, etc.), and draw upon data from neighboring strata to enhance the parameter learning of each sub-problem. They have been widely applied in machine learning and signal processing problems, including but not limited to time series forecasting, representation learning, graph clustering, max-margin classification, and general few-shot learning. Nevertheless, existing works on LRSM have either assumed a known graph or are restricted to specific applications. In this paper, we start by showing the importance and sensitivity of graph weights in LRSM, and provably show that the sensitivity can be arbitrarily large when the parameter scales and sample sizes are heavily imbalanced across nodes. We then propose a generic approach to jointly learn the graph while fitting the model parameters by solving a single optimization problem. We interpret the proposed formulation from both a graph connectivity viewpoint and an end-to-end Bayesian perspective, and propose an efficient algorithm to solve the problem. Convergence guarantees of the proposed optimization algorithm is also provided despite the lack of global strongly smoothness of the Laplacian regularization term typically required in the existing literature, which may be of independent interest. Finally, we illustrate the efficiency of our approach compared to existing methods by various real-world numerical examples.