Factor Fitting, Rank Allocation, and Partitioning in Multilevel Low Rank Matrices

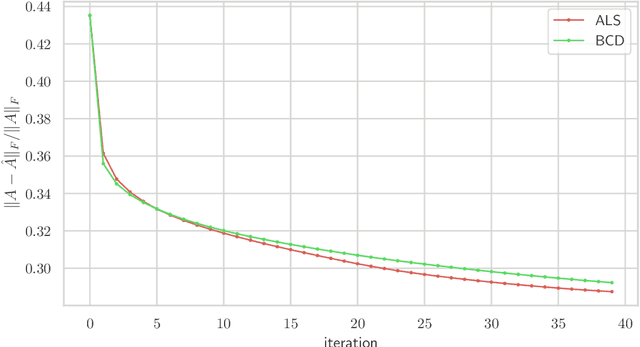
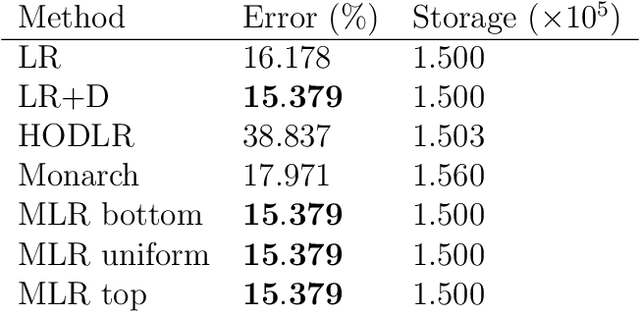
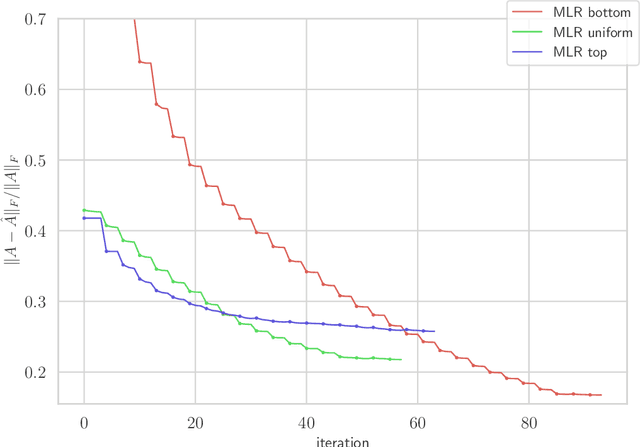
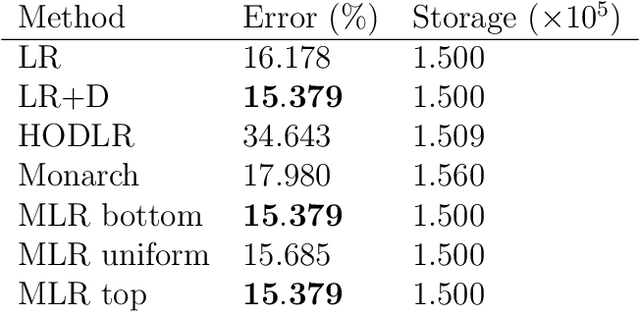
We consider multilevel low rank (MLR) matrices, defined as a row and column permutation of a sum of matrices, each one a block diagonal refinement of the previous one, with all blocks low rank given in factored form. MLR matrices extend low rank matrices but share many of their properties, such as the total storage required and complexity of matrix-vector multiplication. We address three problems that arise in fitting a given matrix by an MLR matrix in the Frobenius norm. The first problem is factor fitting, where we adjust the factors of the MLR matrix. The second is rank allocation, where we choose the ranks of the blocks in each level, subject to the total rank having a given value, which preserves the total storage needed for the MLR matrix. The final problem is to choose the hierarchical partition of rows and columns, along with the ranks and factors. This paper is accompanied by an open source package that implements the proposed methods.