Pre-validation Revisited

Pre-validation is a way to build prediction model with two datasets of significantly different feature dimensions. Previous work showed that the asymptotic distribution of test statistic for the pre-validated predictor deviated from a standard Normal, hence will lead to issues in hypothesis tests. In this paper, we revisited the pre-validation procedure and extended the problem formulation without any independence assumption on the two feature sets. We proposed not only an analytical distribution of the test statistics for pre-validated predictor under certain models, but also a generic bootstrap procedure to conduct inference. We showed properties and benefits of pre-validation in prediction, inference and error estimation by simulation and various applications, including analysis of a breast cancer study and a synthetic GWAS example.

Fitting Multilevel Factor Models

We examine a special case of the multilevel factor model, with covariance given by multilevel low rank (MLR) matrix~\cite{parshakova2023factor}. We develop a novel, fast implementation of the expectation-maximization (EM) algorithm, tailored for multilevel factor models, to maximize the likelihood of the observed data. This method accommodates any hierarchical structure and maintains linear time and storage complexities per iteration. This is achieved through a new efficient technique for computing the inverse of the positive definite MLR matrix. We show that the inverse of an invertible PSD MLR matrix is also an MLR matrix with the same sparsity in factors, and we use the recursive Sherman-Morrison-Woodbury matrix identity to obtain the factors of the inverse. Additionally, we present an algorithm that computes the Cholesky factorization of an expanded matrix with linear time and space complexities, yielding the covariance matrix as its Schur complement. This paper is accompanied by an open-source package that implements the proposed methods.

Scalable recommender system based on factor analysis

Recommender systems have become crucial in the modern digital landscape, where personalized content, products, and services are essential for enhancing user experience. This paper explores statistical models for recommender systems, focusing on crossed random effects models and factor analysis. We extend the crossed random effects model to include random slopes, enabling the capture of varying covariate effects among users and items. Additionally, we investigate the use of factor analysis in recommender systems, particularly for settings with incomplete data. The paper also discusses scalable solutions using the Expectation Maximization (EM) and variational EM algorithms for parameter estimation, highlighting the application of these models to predict user-item interactions effectively.

MMIL: A novel algorithm for disease associated cell type discovery

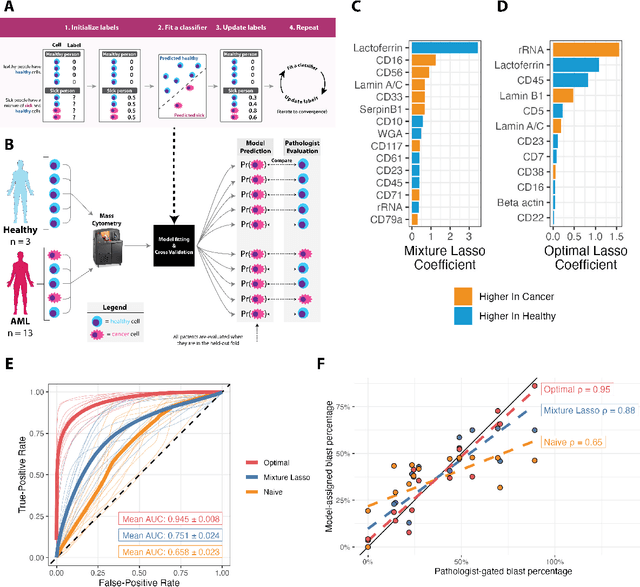
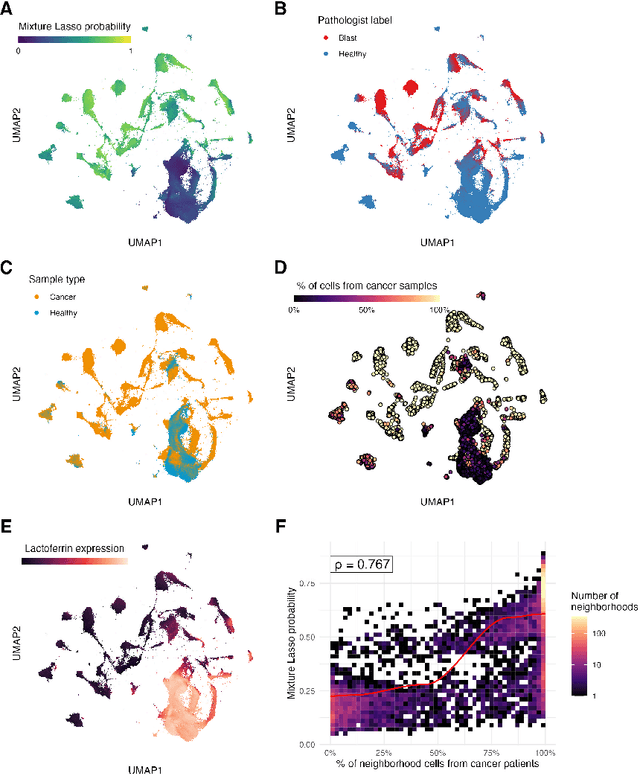
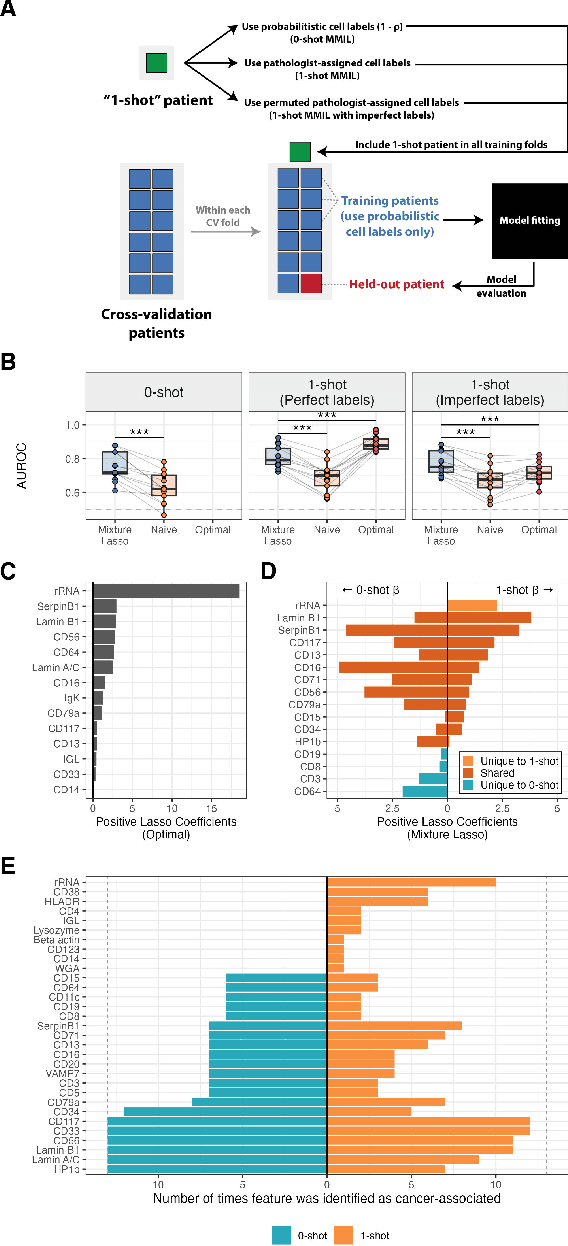
Single-cell datasets often lack individual cell labels, making it challenging to identify cells associated with disease. To address this, we introduce Mixture Modeling for Multiple Instance Learning (MMIL), an expectation maximization method that enables the training and calibration of cell-level classifiers using patient-level labels. Our approach can be used to train e.g. lasso logistic regression models, gradient boosted trees, and neural networks. When applied to clinically-annotated, primary patient samples in Acute Myeloid Leukemia (AML) and Acute Lymphoblastic Leukemia (ALL), our method accurately identifies cancer cells, generalizes across tissues and treatment timepoints, and selects biologically relevant features. In addition, MMIL is capable of incorporating cell labels into model training when they are known, providing a powerful framework for leveraging both labeled and unlabeled data simultaneously. Mixture Modeling for MIL offers a novel approach for cell classification, with significant potential to advance disease understanding and management, especially in scenarios with unknown gold-standard labels and high dimensionality.

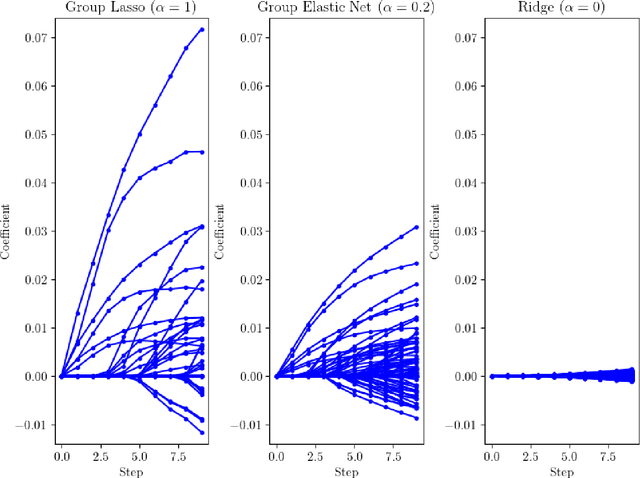
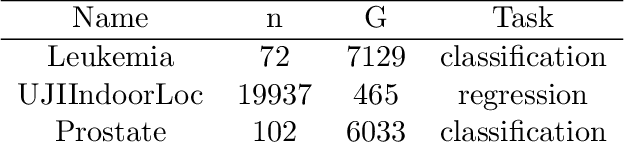
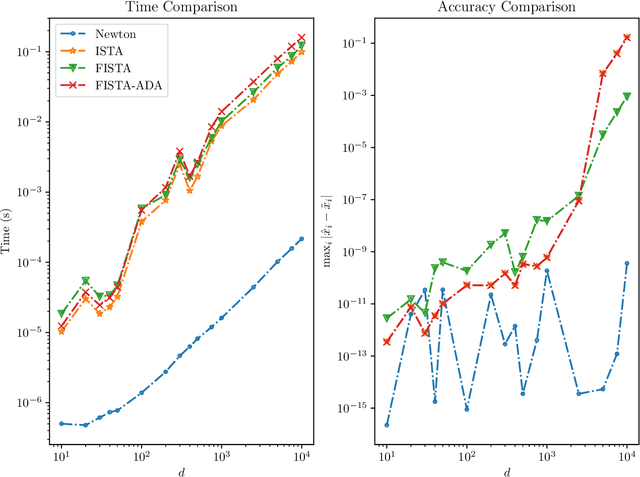
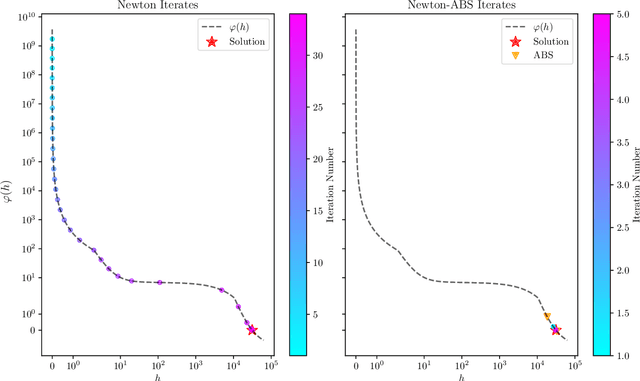
A Fast and Scalable Pathwise-Solver for Group Lasso and Elastic Net Penalized Regression via Block-Coordinate Descent

We develop fast and scalable algorithms based on block-coordinate descent to solve the group lasso and the group elastic net for generalized linear models along a regularization path. Special attention is given when the loss is the usual least squares loss (Gaussian loss). We show that each block-coordinate update can be solved efficiently using Newton's method and further improved using an adaptive bisection method, solving these updates with a quadratic convergence rate. Our benchmarks show that our package adelie performs 3 to 10 times faster than the next fastest package on a wide array of both simulated and real datasets. Moreover, we demonstrate that our package is a competitive lasso solver as well, matching the performance of the popular lasso package glmnet.

Using Pre-training and Interaction Modeling for ancestry-specific disease prediction in UK Biobank

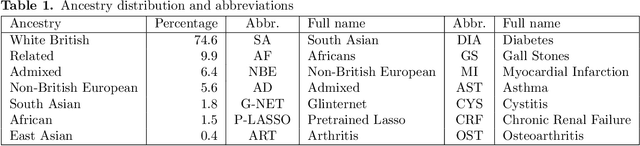
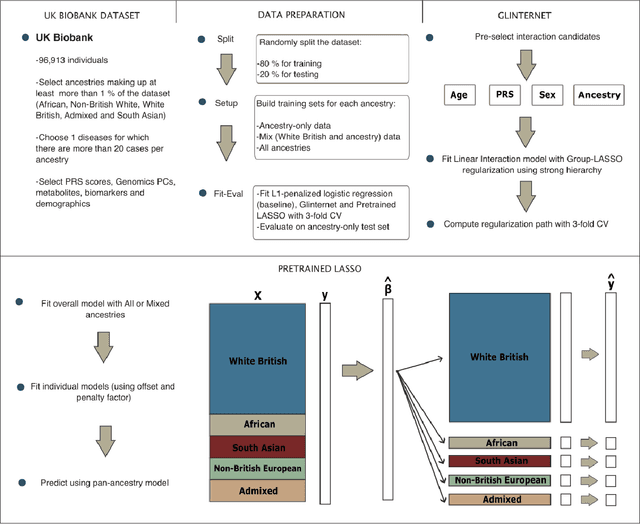
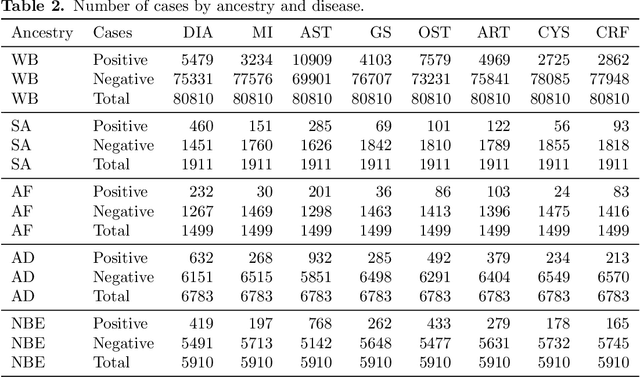
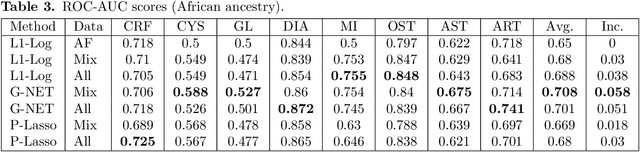
Recent genome-wide association studies (GWAS) have uncovered the genetic basis of complex traits, but show an under-representation of non-European descent individuals, underscoring a critical gap in genetic research. Here, we assess whether we can improve disease prediction across diverse ancestries using multiomic data. We evaluate the performance of Group-LASSO INTERaction-NET (glinternet) and pretrained lasso in disease prediction focusing on diverse ancestries in the UK Biobank. Models were trained on data from White British and other ancestries and validated across a cohort of over 96,000 individuals for 8 diseases. Out of 96 models trained, we report 16 with statistically significant incremental predictive performance in terms of ROC-AUC scores. These findings suggest that advanced statistical methods that borrow information across multiple ancestries may improve disease risk prediction, but with limited benefit.

Factor Fitting, Rank Allocation, and Partitioning in Multilevel Low Rank Matrices

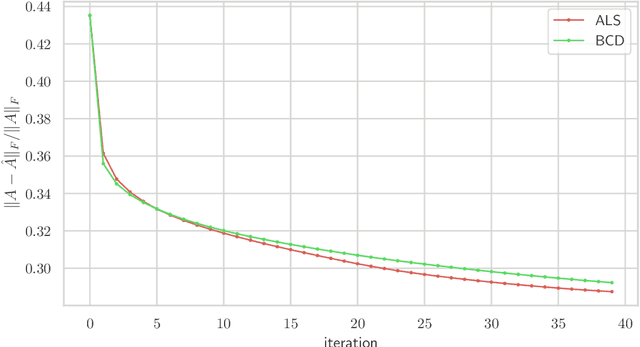
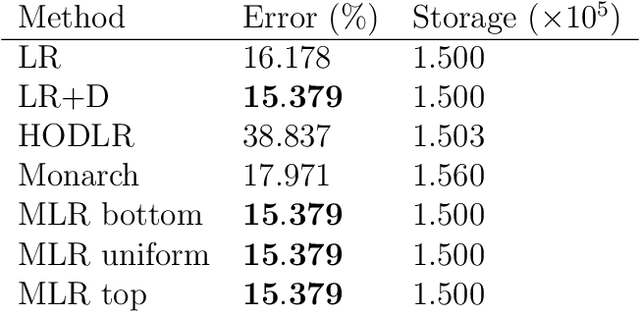
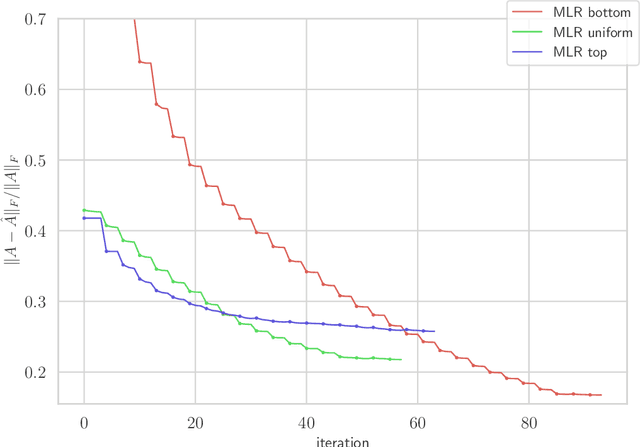
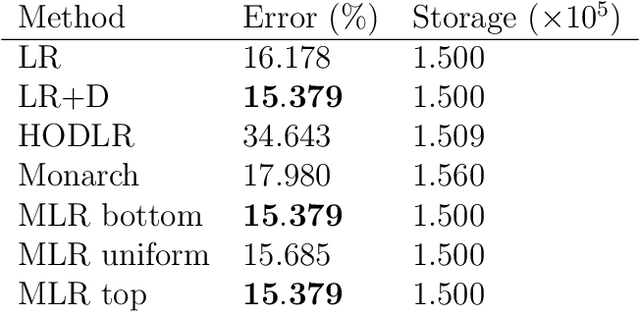
We consider multilevel low rank (MLR) matrices, defined as a row and column permutation of a sum of matrices, each one a block diagonal refinement of the previous one, with all blocks low rank given in factored form. MLR matrices extend low rank matrices but share many of their properties, such as the total storage required and complexity of matrix-vector multiplication. We address three problems that arise in fitting a given matrix by an MLR matrix in the Frobenius norm. The first problem is factor fitting, where we adjust the factors of the MLR matrix. The second is rank allocation, where we choose the ranks of the blocks in each level, subject to the total rank having a given value, which preserves the total storage needed for the MLR matrix. The final problem is to choose the hierarchical partition of rows and columns, along with the ranks and factors. This paper is accompanied by an open source package that implements the proposed methods.

A Statistical View of Column Subset Selection

We consider the problem of selecting a small subset of representative variables from a large dataset. In the computer science literature, this dimensionality reduction problem is typically formalized as Column Subset Selection (CSS). Meanwhile, the typical statistical formalization is to find an information-maximizing set of Principal Variables. This paper shows that these two approaches are equivalent, and moreover, both can be viewed as maximum likelihood estimation within a certain semi-parametric model. Using these connections, we show how to efficiently (1) perform CSS using only summary statistics from the original dataset; (2) perform CSS in the presence of missing and/or censored data; and (3) select the subset size for CSS in a hypothesis testing framework.

RbX: Region-based explanations of prediction models

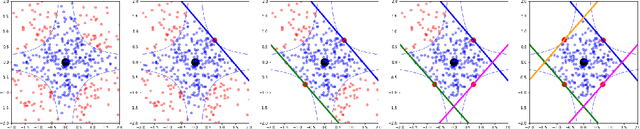
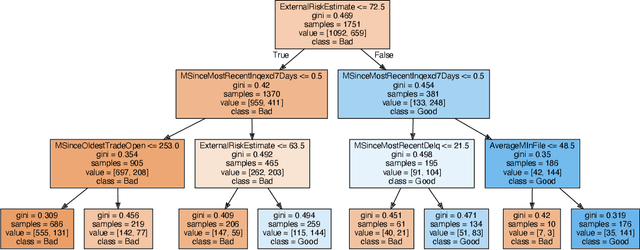
We introduce region-based explanations (RbX), a novel, model-agnostic method to generate local explanations of scalar outputs from a black-box prediction model using only query access. RbX is based on a greedy algorithm for building a convex polytope that approximates a region of feature space where model predictions are close to the prediction at some target point. This region is fully specified by the user on the scale of the predictions, rather than on the scale of the features. The geometry of this polytope - specifically the change in each coordinate necessary to escape the polytope - quantifies the local sensitivity of the predictions to each of the features. These "escape distances" can then be standardized to rank the features by local importance. RbX is guaranteed to satisfy a "sparsity axiom," which requires that features which do not enter into the prediction model are assigned zero importance. At the same time, real data examples and synthetic experiments show how RbX can more readily detect all locally relevant features than existing methods.

Weighted Low Rank Matrix Approximation and Acceleration

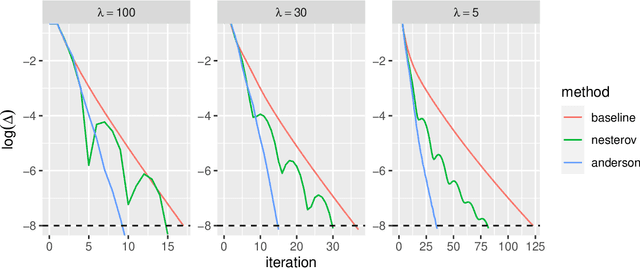
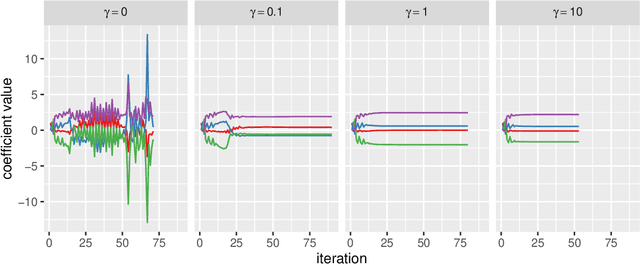
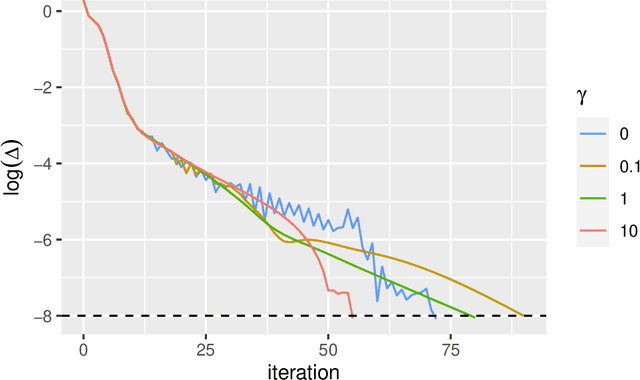
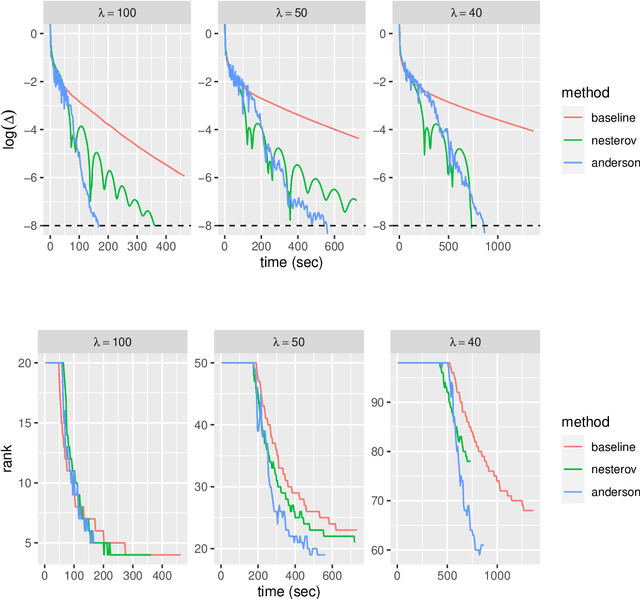
Low-rank matrix approximation is one of the central concepts in machine learning, with applications in dimension reduction, de-noising, multivariate statistical methodology, and many more. A recent extension to LRMA is called low-rank matrix completion (LRMC). It solves the LRMA problem when some observations are missing and is especially useful for recommender systems. In this paper, we consider an element-wise weighted generalization of LRMA. The resulting weighted low-rank matrix approximation technique therefore covers LRMC as a special case with binary weights. WLRMA has many applications. For example, it is an essential component of GLM optimization algorithms, where an exponential family is used to model the entries of a matrix, and the matrix of natural parameters admits a low-rank structure. We propose an algorithm for solving the weighted problem, as well as two acceleration techniques. Further, we develop a non-SVD modification of the proposed algorithm that is able to handle extremely high-dimensional data. We compare the performance of all the methods on a small simulation example as well as a real-data application.