Semiparametric conformal prediction

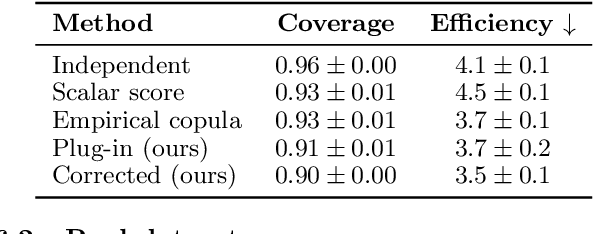
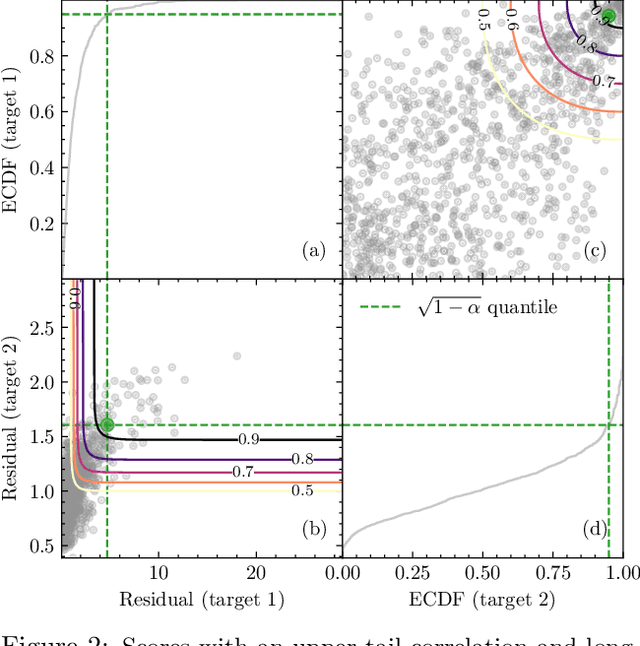
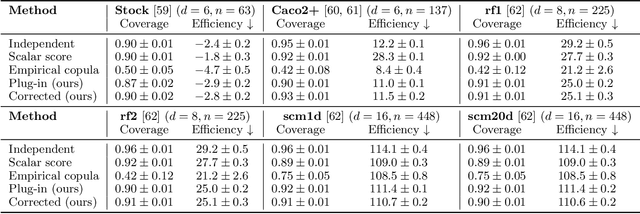
Many risk-sensitive applications require well-calibrated prediction sets over multiple, potentially correlated target variables, for which the prediction algorithm may report correlated non-conformity scores. In this work, we treat the scores as random vectors and aim to construct the prediction set accounting for their joint correlation structure. Drawing from the rich literature on multivariate quantiles and semiparametric statistics, we propose an algorithm to estimate the $1-\alpha$ quantile of the scores, where $\alpha$ is the user-specified miscoverage rate. In particular, we flexibly estimate the joint cumulative distribution function (CDF) of the scores using nonparametric vine copulas and improve the asymptotic efficiency of the quantile estimate using its influence function. The vine decomposition allows our method to scale well to a large number of targets. We report desired coverage and competitive efficiency on a range of real-world regression problems, including those with missing-at-random labels in the calibration set.

MMIL: A novel algorithm for disease associated cell type discovery

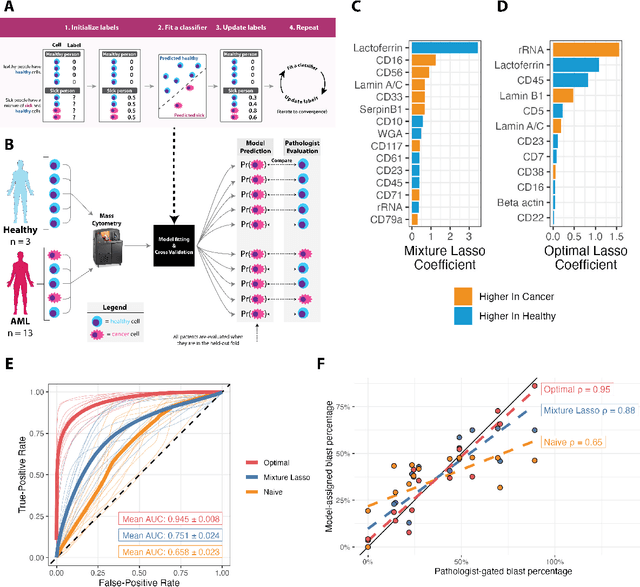
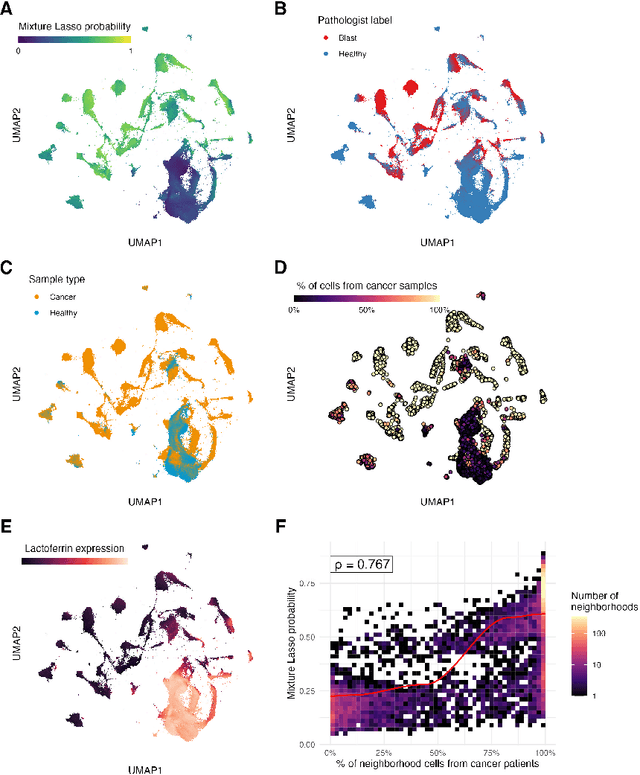
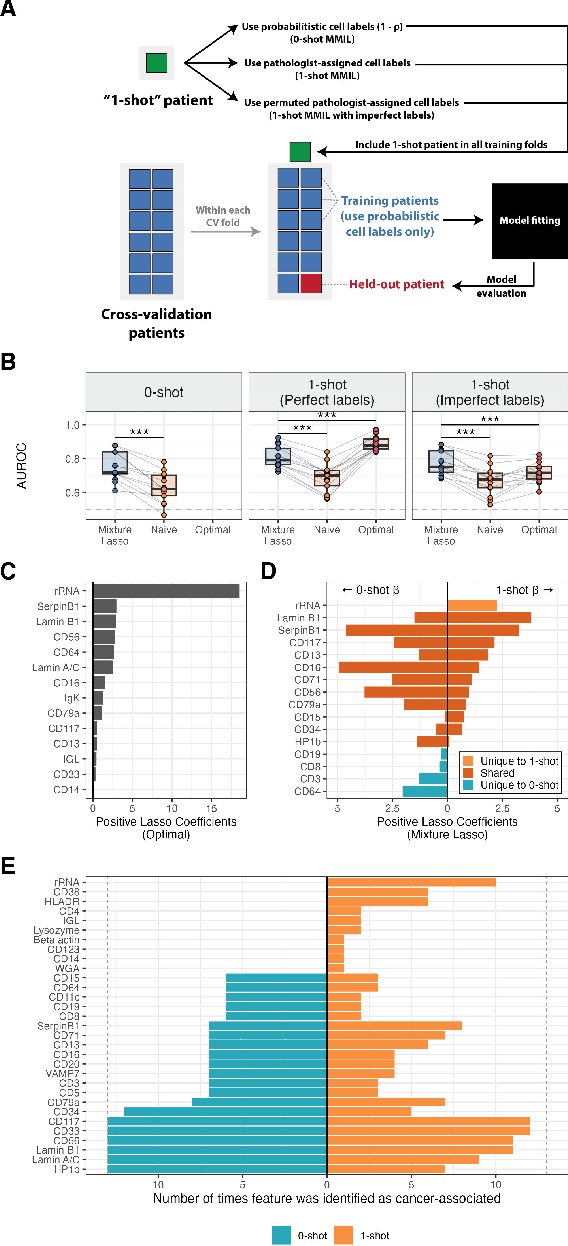
Single-cell datasets often lack individual cell labels, making it challenging to identify cells associated with disease. To address this, we introduce Mixture Modeling for Multiple Instance Learning (MMIL), an expectation maximization method that enables the training and calibration of cell-level classifiers using patient-level labels. Our approach can be used to train e.g. lasso logistic regression models, gradient boosted trees, and neural networks. When applied to clinically-annotated, primary patient samples in Acute Myeloid Leukemia (AML) and Acute Lymphoblastic Leukemia (ALL), our method accurately identifies cancer cells, generalizes across tissues and treatment timepoints, and selects biologically relevant features. In addition, MMIL is capable of incorporating cell labels into model training when they are known, providing a powerful framework for leveraging both labeled and unlabeled data simultaneously. Mixture Modeling for MIL offers a novel approach for cell classification, with significant potential to advance disease understanding and management, especially in scenarios with unknown gold-standard labels and high dimensionality.

Using Pre-training and Interaction Modeling for ancestry-specific disease prediction in UK Biobank

Recent genome-wide association studies (GWAS) have uncovered the genetic basis of complex traits, but show an under-representation of non-European descent individuals, underscoring a critical gap in genetic research. Here, we assess whether we can improve disease prediction across diverse ancestries using multiomic data. We evaluate the performance of Group-LASSO INTERaction-NET (glinternet) and pretrained lasso in disease prediction focusing on diverse ancestries in the UK Biobank. Models were trained on data from White British and other ancestries and validated across a cohort of over 96,000 individuals for 8 diseases. Out of 96 models trained, we report 16 with statistically significant incremental predictive performance in terms of ROC-AUC scores. These findings suggest that advanced statistical methods that borrow information across multiple ancestries may improve disease risk prediction, but with limited benefit.

FastCPH: Efficient Survival Analysis for Neural Networks

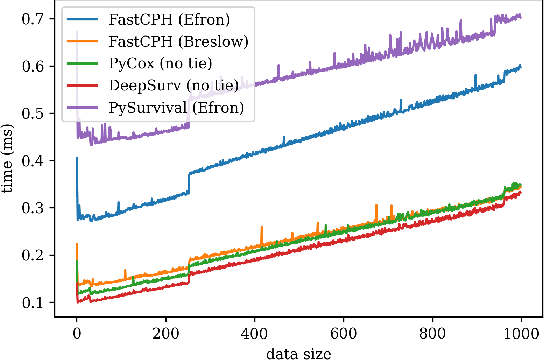
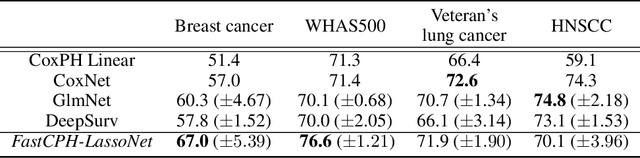
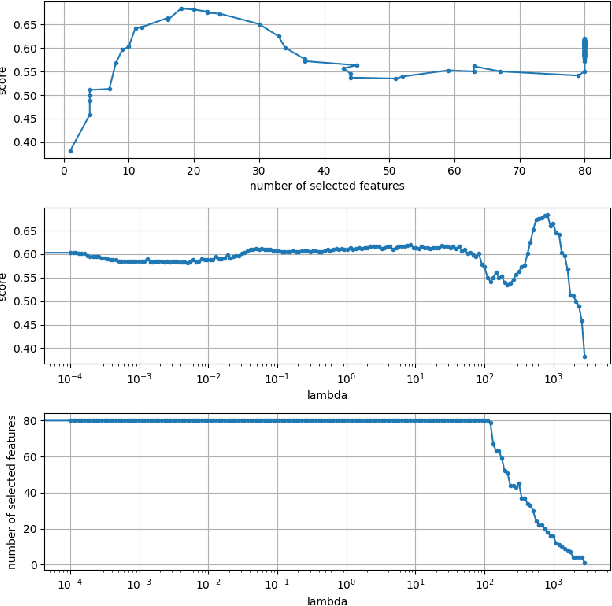
The Cox proportional hazards model is a canonical method in survival analysis for prediction of the life expectancy of a patient given clinical or genetic covariates -- it is a linear model in its original form. In recent years, several methods have been proposed to generalize the Cox model to neural networks, but none of these are both numerically correct and computationally efficient. We propose FastCPH, a new method that runs in linear time and supports both the standard Breslow and Efron methods for tied events. We also demonstrate the performance of FastCPH combined with LassoNet, a neural network that provides interpretability through feature sparsity, on survival datasets. The final procedure is efficient, selects useful covariates and outperforms existing CoxPH approaches.

Confidence intervals for the Cox model test error from cross-validation

Cross-validation (CV) is one of the most widely used techniques in statistical learning for estimating the test error of a model, but its behavior is not yet fully understood. It has been shown that standard confidence intervals for test error using estimates from CV may have coverage below nominal levels. This phenomenon occurs because each sample is used in both the training and testing procedures during CV and as a result, the CV estimates of the errors become correlated. Without accounting for this correlation, the estimate of the variance is smaller than it should be. One way to mitigate this issue is by estimating the mean squared error of the prediction error instead using nested CV. This approach has been shown to achieve superior coverage compared to intervals derived from standard CV. In this work, we generalize the nested CV idea to the Cox proportional hazards model and explore various choices of test error for this setting.

Cooperative learning for multi-view analysis

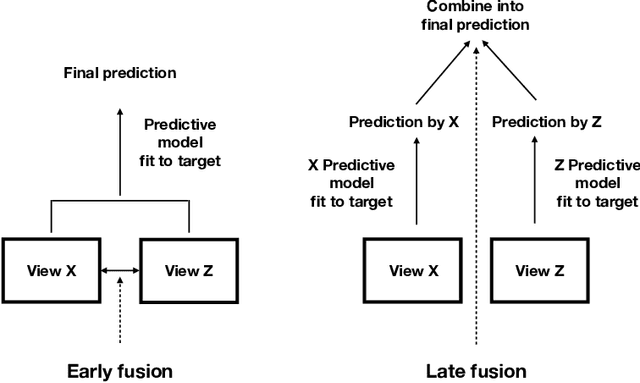
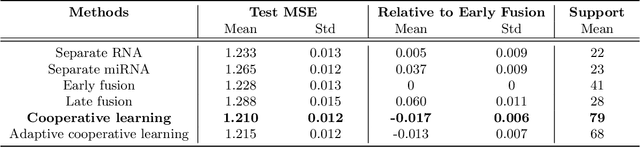
We propose a new method for supervised learning with multiple sets of features ("views"). Cooperative learning combines the usual squared error loss of predictions with an "agreement" penalty to encourage the predictions from different data views to agree. By varying the weight of the agreement penalty, we get a continuum of solutions that include the well-known early and late fusion approaches. Cooperative learning chooses the degree of agreement (or fusion) in an adaptive manner, using a validation set or cross-validation to estimate test set prediction error. One version of our fitting procedure is modular, where one can choose different fitting mechanisms (e.g. lasso, random forests, boosting, neural networks) appropriate for different data views. In the setting of cooperative regularized linear regression, the method combines the lasso penalty with the agreement penalty. The method can be especially powerful when the different data views share some underlying relationship in their signals that we aim to strengthen, while each view has its idiosyncratic noise that we aim to reduce. We illustrate the effectiveness of our proposed method on simulated and real data examples.

Cross-validation: what does it estimate and how well does it do it?

Cross-validation is a widely-used technique to estimate prediction error, but its behavior is complex and not fully understood. Ideally, one would like to think that cross-validation estimates the prediction error for the model at hand, fit to the training data. We prove that this is not the case for the linear model fit by ordinary least squares; rather it estimates the average prediction error of models fit on other unseen training sets drawn from the same population. We further show that this phenomenon occurs for most popular estimates of prediction error, including data splitting, bootstrapping, and Mallow's Cp. Next, the standard confidence intervals for prediction error derived from cross-validation may have coverage far below the desired level. Because each data point is used for both training and testing, there are correlations among the measured accuracies for each fold, and so the usual estimate of variance is too small. We introduce a nested cross-validation scheme to estimate this variance more accurately, and show empirically that this modification leads to intervals with approximately correct coverage in many examples where traditional cross-validation intervals fail. Lastly, our analysis also shows that when producing confidence intervals for prediction accuracy with simple data splitting, one should not re-fit the model on the combined data, since this invalidates the confidence intervals.

Feature-weighted elastic net: using "features of features" for better prediction

In some supervised learning settings, the practitioner might have additional information on the features used for prediction. We propose a new method which leverages this additional information for better prediction. The method, which we call the feature-weighted elastic net ("fwelnet"), uses these "features of features" to adapt the relative penalties on the feature coefficients in the elastic net penalty. In our simulations, fwelnet outperforms the lasso in terms of test mean squared error and usually gives an improvement in true positive rate or false positive rate for feature selection. We also apply this method to early prediction of preeclampsia, where fwelnet outperforms the lasso in terms of 10-fold cross-validated area under the curve (0.86 vs. 0.80). We also provide a connection between fwelnet and the group lasso and suggest how fwelnet might be used for multi-task learning.

Reluctant generalized additive modeling

Sparse generalized additive models (GAMs) are an extension of sparse generalized linear models which allow a model's prediction to vary non-linearly with an input variable. This enables the data analyst build more accurate models, especially when the linearity assumption is known to be a poor approximation of reality. Motivated by reluctant interaction modeling (Yu et al. 2019), we propose a multi-stage algorithm, called $\textit{reluctant generalized additive modeling (RGAM)}$, that can fit sparse generalized additive models at scale. It is guided by the principle that, if all else is equal, one should prefer a linear feature over a non-linear feature. Unlike existing methods for sparse GAMs, RGAM can be extended easily to binary, count and survival data. We demonstrate the method's effectiveness on real and simulated examples.

A neural network with feature sparsity

We propose a neural network model, with a separate linear (residual) term, that explicitly bounds the input layer weights for a feature by the linear weight for that feature. The model can be seen as a modification of so-called residual neural networks to produce a path of models that are feature-sparse, that is, use only a subset of the features. This is analogous to the solution path from the usual Lasso ($\ell_1$-regularized) linear regression. We call the proposed procedure "LassoNet" and develop a projected proximal gradient algorithm for its optimization. This approach can sometimes give as low or lower test error than a standard neural network, and its feature selection provides more interpretable solutions. We illustrate the method using both simulated and real data examples, and show that it is often able to achieve competitive performance with a much smaller number of input features.