Ji Won Park
for the LSST Dark Energy Science Collaboration
Reliable algorithm selection for machine learning-guided design
Mar 26, 2025Abstract:Algorithms for machine learning-guided design, or design algorithms, use machine learning-based predictions to propose novel objects with desired property values. Given a new design task -- for example, to design novel proteins with high binding affinity to a therapeutic target -- one must choose a design algorithm and specify any hyperparameters and predictive and/or generative models involved. How can these decisions be made such that the resulting designs are successful? This paper proposes a method for design algorithm selection, which aims to select design algorithms that will produce a distribution of design labels satisfying a user-specified success criterion -- for example, that at least ten percent of designs' labels exceed a threshold. It does so by combining designs' predicted property values with held-out labeled data to reliably forecast characteristics of the label distributions produced by different design algorithms, building upon techniques from prediction-powered inference. The method is guaranteed with high probability to return design algorithms that yield successful label distributions (or the null set if none exist), if the density ratios between the design and labeled data distributions are known. We demonstrate the method's effectiveness in simulated protein and RNA design tasks, in settings with either known or estimated density ratios.
Supervised Contrastive Block Disentanglement
Feb 11, 2025



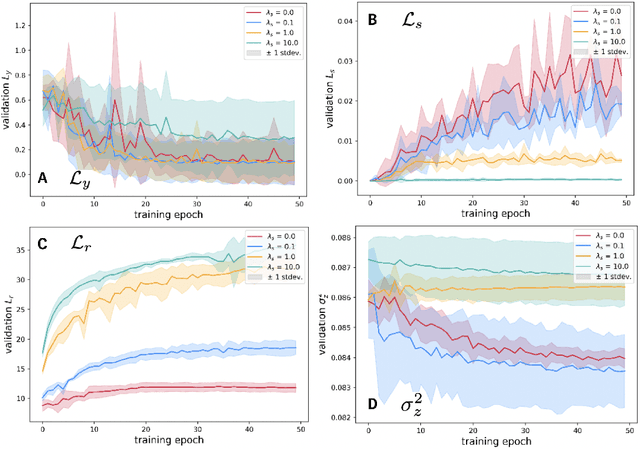
Abstract:Real-world datasets often combine data collected under different experimental conditions. This yields larger datasets, but also introduces spurious correlations that make it difficult to model the phenomena of interest. We address this by learning two embeddings to independently represent the phenomena of interest and the spurious correlations. The embedding representing the phenomena of interest is correlated with the target variable $y$, and is invariant to the environment variable $e$. In contrast, the embedding representing the spurious correlations is correlated with $e$. The invariance to $e$ is difficult to achieve on real-world datasets. Our primary contribution is an algorithm called Supervised Contrastive Block Disentanglement (SCBD) that effectively enforces this invariance. It is based purely on Supervised Contrastive Learning, and applies to real-world data better than existing approaches. We empirically validate SCBD on two challenging problems. The first problem is domain generalization, where we achieve strong performance on a synthetic dataset, as well as on Camelyon17-WILDS. We introduce a single hyperparameter $\alpha$ to control the degree of invariance to $e$. When we increase $\alpha$ to strengthen the degree of invariance, out-of-distribution performance improves at the expense of in-distribution performance. The second problem is batch correction, in which we apply SCBD to preserve biological signal and remove inter-well batch effects when modeling single-cell perturbations from 26 million Optical Pooled Screening images.
Semiparametric conformal prediction
Nov 04, 2024
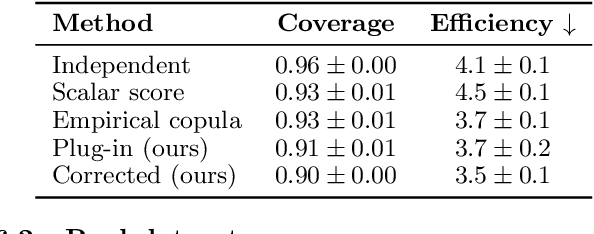
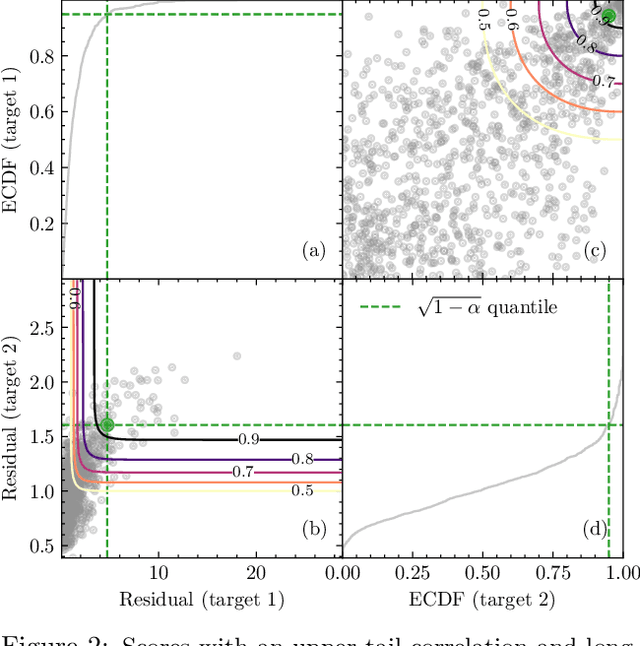
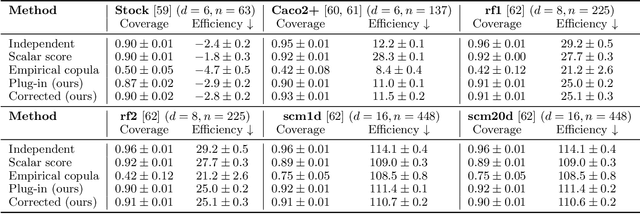
Abstract:Many risk-sensitive applications require well-calibrated prediction sets over multiple, potentially correlated target variables, for which the prediction algorithm may report correlated non-conformity scores. In this work, we treat the scores as random vectors and aim to construct the prediction set accounting for their joint correlation structure. Drawing from the rich literature on multivariate quantiles and semiparametric statistics, we propose an algorithm to estimate the $1-\alpha$ quantile of the scores, where $\alpha$ is the user-specified miscoverage rate. In particular, we flexibly estimate the joint cumulative distribution function (CDF) of the scores using nonparametric vine copulas and improve the asymptotic efficiency of the quantile estimate using its influence function. The vine decomposition allows our method to scale well to a large number of targets. We report desired coverage and competitive efficiency on a range of real-world regression problems, including those with missing-at-random labels in the calibration set.
Blind Biological Sequence Denoising with Self-Supervised Set Learning
Sep 04, 2023Abstract:Biological sequence analysis relies on the ability to denoise the imprecise output of sequencing platforms. We consider a common setting where a short sequence is read out repeatedly using a high-throughput long-read platform to generate multiple subreads, or noisy observations of the same sequence. Denoising these subreads with alignment-based approaches often fails when too few subreads are available or error rates are too high. In this paper, we propose a novel method for blindly denoising sets of sequences without directly observing clean source sequence labels. Our method, Self-Supervised Set Learning (SSSL), gathers subreads together in an embedding space and estimates a single set embedding as the midpoint of the subreads in both the latent and sequence spaces. This set embedding represents the "average" of the subreads and can be decoded into a prediction of the clean sequence. In experiments on simulated long-read DNA data, SSSL methods denoise small reads of $\leq 6$ subreads with 17% fewer errors and large reads of $>6$ subreads with 8% fewer errors compared to the best baseline. On a real dataset of antibody sequences, SSSL improves over baselines on two self-supervised metrics, with a significant improvement on difficult small reads that comprise over 60% of the test set. By accurately denoising these reads, SSSL promises to better realize the potential of high-throughput DNA sequencing data for downstream scientific applications.
BOtied: Multi-objective Bayesian optimization with tied multivariate ranks
Jun 01, 2023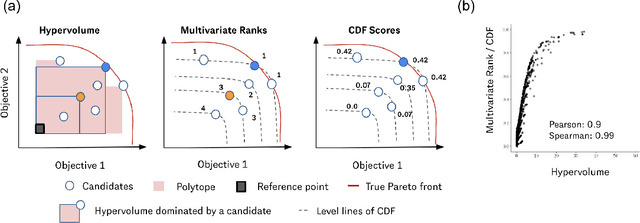
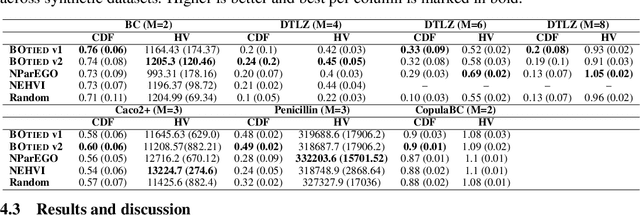
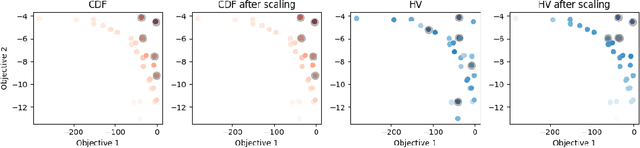
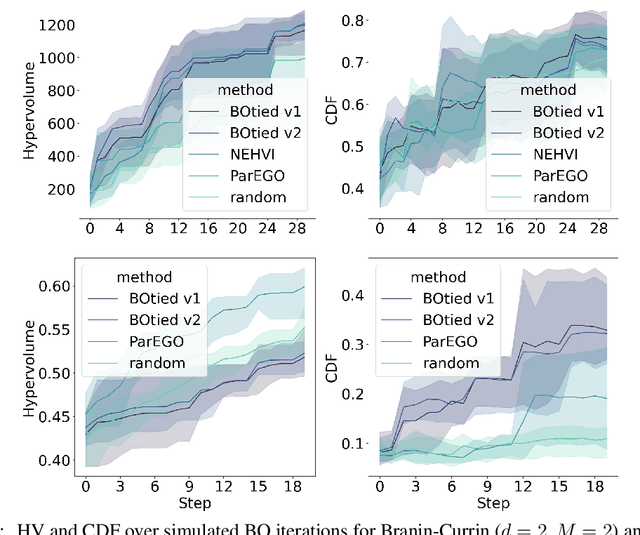
Abstract:Many scientific and industrial applications require joint optimization of multiple, potentially competing objectives. Multi-objective Bayesian optimization (MOBO) is a sample-efficient framework for identifying Pareto-optimal solutions. We show a natural connection between non-dominated solutions and the highest multivariate rank, which coincides with the outermost level line of the joint cumulative distribution function (CDF). We propose the CDF indicator, a Pareto-compliant metric for evaluating the quality of approximate Pareto sets that complements the popular hypervolume indicator. At the heart of MOBO is the acquisition function, which determines the next candidate to evaluate by navigating the best compromises among the objectives. Multi-objective acquisition functions that rely on box decomposition of the objective space, such as the expected hypervolume improvement (EHVI) and entropy search, scale poorly to a large number of objectives. We propose an acquisition function, called BOtied, based on the CDF indicator. BOtied can be implemented efficiently with copulas, a statistical tool for modeling complex, high-dimensional distributions. We benchmark BOtied against common acquisition functions, including EHVI and random scalarization (ParEGO), in a series of synthetic and real-data experiments. BOtied performs on par with the baselines across datasets and metrics while being computationally efficient.
Chain of Log-Concave Markov Chains
May 31, 2023Abstract:Markov chain Monte Carlo (MCMC) is a class of general-purpose algorithms for sampling from unnormalized densities. There are two well-known problems facing MCMC in high dimensions: (i) The distributions of interest are concentrated in pockets separated by large regions with small probability mass, and (ii) The log-concave pockets themselves are typically ill-conditioned. We introduce a framework to tackle these problems using isotropic Gaussian smoothing. We prove one can always decompose sampling from a density (minimal assumptions made on the density) into a sequence of sampling from log-concave conditional densities via accumulation of noisy measurements with equal noise levels. This construction keeps track of a history of samples, making it non-Markovian as a whole, but the history only shows up in the form of an empirical mean, making the memory footprint minimal. Our sampling algorithm generalizes walk-jump sampling [1]. The "walk" phase becomes a (non-Markovian) chain of log-concave Langevin chains. The "jump" from the accumulated measurements is obtained by empirical Bayes. We study our sampling algorithm quantitatively using the 2-Wasserstein metric and compare it with various Langevin MCMC algorithms. We also report a remarkable capacity of our algorithm to "tunnel" between modes of a distribution.
SupSiam: Non-contrastive Auxiliary Loss for Learning from Molecular Conformers
Feb 15, 2023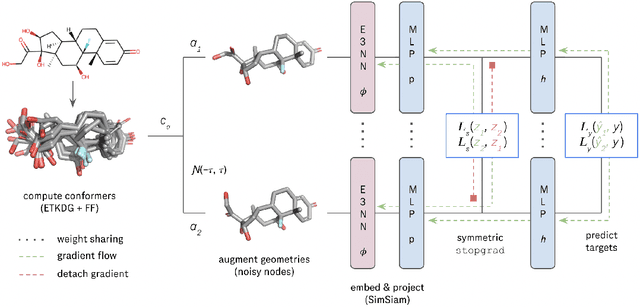


Abstract:We investigate Siamese networks for learning related embeddings for augmented samples of molecular conformers. We find that a non-contrastive (positive-pair only) auxiliary task aids in supervised training of Euclidean neural networks (E3NNs) and increases manifold smoothness (MS) around point-cloud geometries. We demonstrate this property for multiple drug-activity prediction tasks while maintaining relevant performance metrics, and propose an extension of MS to probabilistic and regression settings. We provide an analysis of representation collapse, finding substantial effects of task-weighting, latent dimension, and regularization. We expect the presented protocol to aid in the development of reliable E3NNs from molecular conformers, even for small-data drug discovery programs.
Hierarchical Inference of the Lensing Convergence from Photometric Catalogs with Bayesian Graph Neural Networks
Nov 15, 2022Abstract:We present a Bayesian graph neural network (BGNN) that can estimate the weak lensing convergence ($\kappa$) from photometric measurements of galaxies along a given line of sight. The method is of particular interest in strong gravitational time delay cosmography (TDC), where characterizing the "external convergence" ($\kappa_{\rm ext}$) from the lens environment and line of sight is necessary for precise inference of the Hubble constant ($H_0$). Starting from a large-scale simulation with a $\kappa$ resolution of $\sim$1$'$, we introduce fluctuations on galaxy-galaxy lensing scales of $\sim$1$''$ and extract random sightlines to train our BGNN. We then evaluate the model on test sets with varying degrees of overlap with the training distribution. For each test set of 1,000 sightlines, the BGNN infers the individual $\kappa$ posteriors, which we combine in a hierarchical Bayesian model to yield constraints on the hyperparameters governing the population. For a test field well sampled by the training set, the BGNN recovers the population mean of $\kappa$ precisely and without bias, resulting in a contribution to the $H_0$ error budget well under 1\%. In the tails of the training set with sparse samples, the BGNN, which can ingest all available information about each sightline, extracts more $\kappa$ signal compared to a simplified version of the traditional method based on matching galaxy number counts, which is limited by sample variance. Our hierarchical inference pipeline using BGNNs promises to improve the $\kappa_{\rm ext}$ characterization for precision TDC. The implementation of our pipeline is available as a public Python package, Node to Joy.
PropertyDAG: Multi-objective Bayesian optimization of partially ordered, mixed-variable properties for biological sequence design
Oct 08, 2022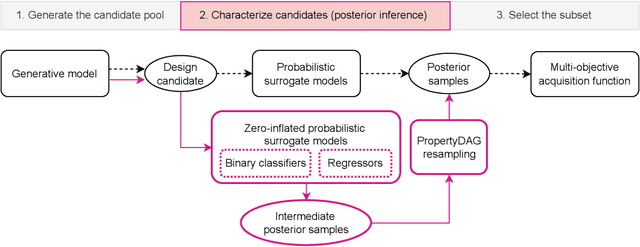
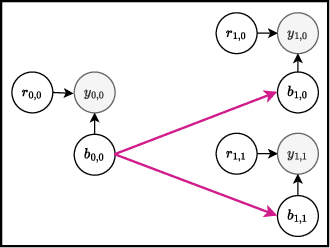
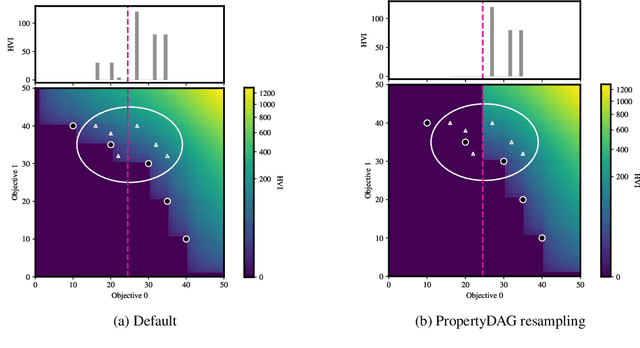
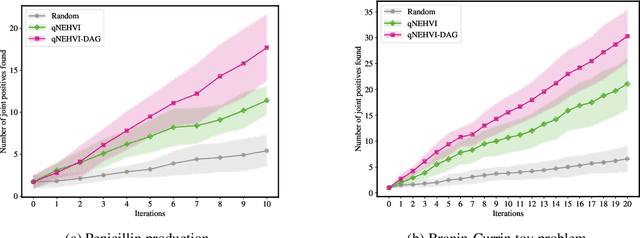
Abstract:Bayesian optimization offers a sample-efficient framework for navigating the exploration-exploitation trade-off in the vast design space of biological sequences. Whereas it is possible to optimize the various properties of interest jointly using a multi-objective acquisition function, such as the expected hypervolume improvement (EHVI), this approach does not account for objectives with a hierarchical dependency structure. We consider a common use case where some regions of the Pareto frontier are prioritized over others according to a specified $\textit{partial ordering}$ in the objectives. For instance, when designing antibodies, we would like to maximize the binding affinity to a target antigen only if it can be expressed in live cell culture -- modeling the experimental dependency in which affinity can only be measured for antibodies that can be expressed and thus produced in viable quantities. In general, we may want to confer a partial ordering to the properties such that each property is optimized conditioned on its parent properties satisfying some feasibility condition. To this end, we present PropertyDAG, a framework that operates on top of the traditional multi-objective BO to impose this desired ordering on the objectives, e.g. expression $\rightarrow$ affinity. We demonstrate its performance over multiple simulated active learning iterations on a penicillin production task, toy numerical problem, and a real-world antibody design task.
Multi-segment preserving sampling for deep manifold sampler
May 09, 2022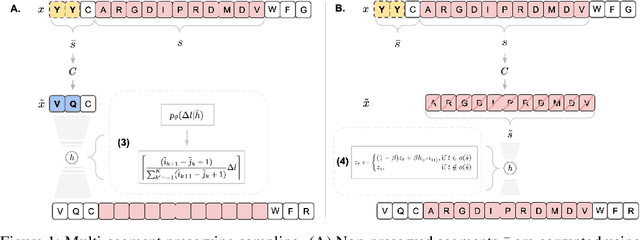

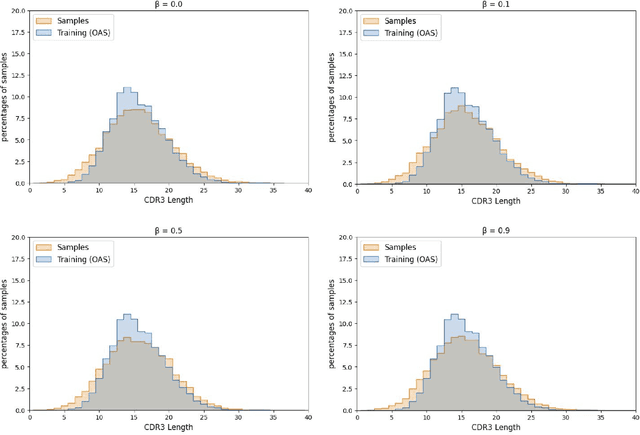
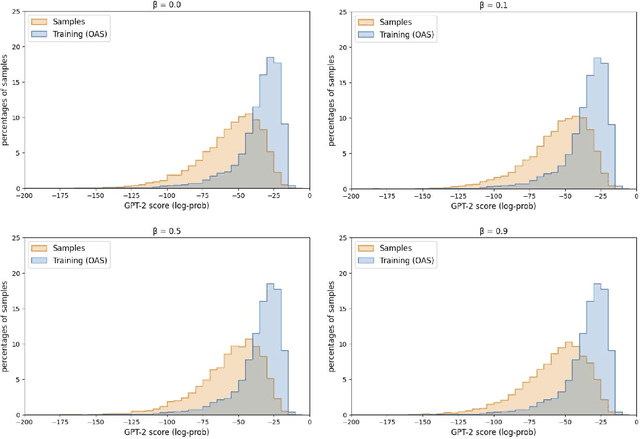
Abstract:Deep generative modeling for biological sequences presents a unique challenge in reconciling the bias-variance trade-off between explicit biological insight and model flexibility. The deep manifold sampler was recently proposed as a means to iteratively sample variable-length protein sequences by exploiting the gradients from a function predictor. We introduce an alternative approach to this guided sampling procedure, multi-segment preserving sampling, that enables the direct inclusion of domain-specific knowledge by designating preserved and non-preserved segments along the input sequence, thereby restricting variation to only select regions. We present its effectiveness in the context of antibody design by training two models: a deep manifold sampler and a GPT-2 language model on nearly six million heavy chain sequences annotated with the IGHV1-18 gene. During sampling, we restrict variation to only the complementarity-determining region 3 (CDR3) of the input. We obtain log probability scores from a GPT-2 model for each sampled CDR3 and demonstrate that multi-segment preserving sampling generates reasonable designs while maintaining the desired, preserved regions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge