Concept Bottleneck Language Models For protein design

We introduce Concept Bottleneck Protein Language Models (CB-pLM), a generative masked language model with a layer where each neuron corresponds to an interpretable concept. Our architecture offers three key benefits: i) Control: We can intervene on concept values to precisely control the properties of generated proteins, achieving a 3 times larger change in desired concept values compared to baselines. ii) Interpretability: A linear mapping between concept values and predicted tokens allows transparent analysis of the model's decision-making process. iii) Debugging: This transparency facilitates easy debugging of trained models. Our models achieve pre-training perplexity and downstream task performance comparable to traditional masked protein language models, demonstrating that interpretability does not compromise performance. While adaptable to any language model, we focus on masked protein language models due to their importance in drug discovery and the ability to validate our model's capabilities through real-world experiments and expert knowledge. We scale our CB-pLM from 24 million to 3 billion parameters, making them the largest Concept Bottleneck Models trained and the first capable of generative language modeling.

Closed-Form Test Functions for Biophysical Sequence Optimization Algorithms

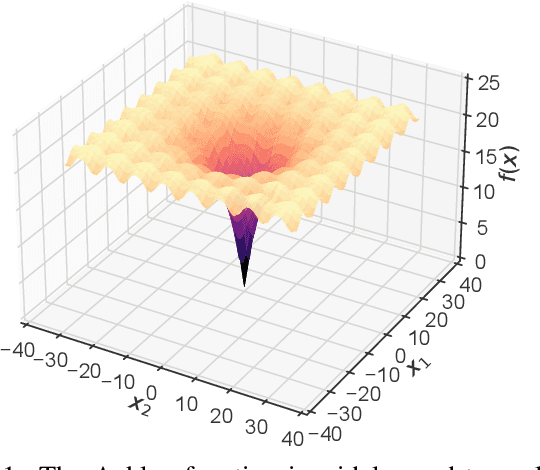
There is a growing body of work seeking to replicate the success of machine learning (ML) on domains like computer vision (CV) and natural language processing (NLP) to applications involving biophysical data. One of the key ingredients of prior successes in CV and NLP was the broad acceptance of difficult benchmarks that distilled key subproblems into approachable tasks that any junior researcher could investigate, but good benchmarks for biophysical domains are rare. This scarcity is partially due to a narrow focus on benchmarks which simulate biophysical data; we propose instead to carefully abstract biophysical problems into simpler ones with key geometric similarities. In particular we propose a new class of closed-form test functions for biophysical sequence optimization, which we call Ehrlich functions. We provide empirical results demonstrating these functions are interesting objects of study and can be non-trivial to solve with a standard genetic optimization baseline.

Conformal Validity Guarantees Exist for Any Data Distribution

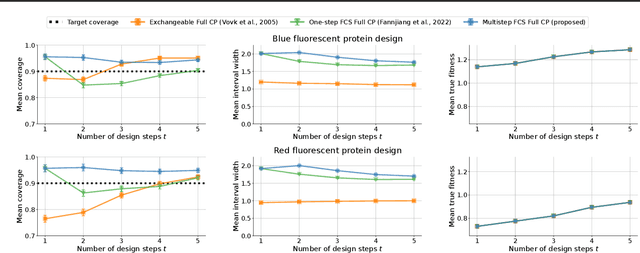
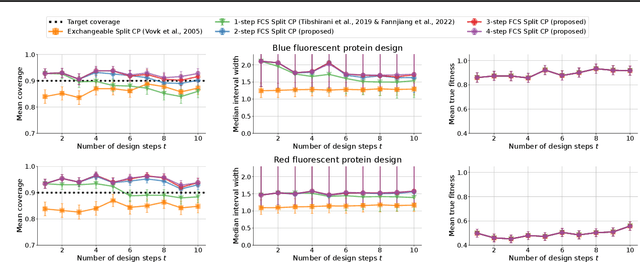
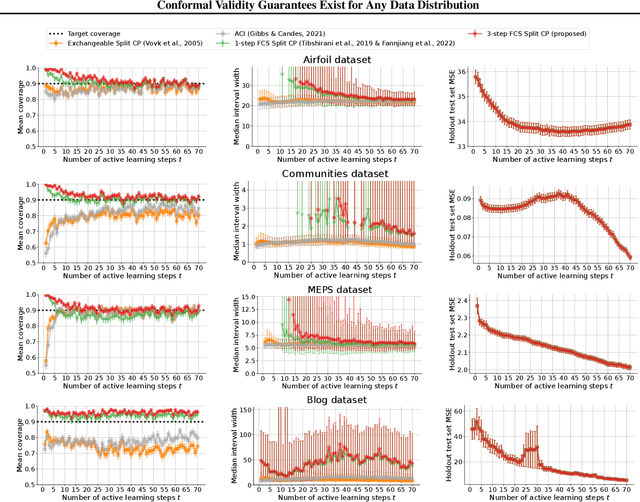
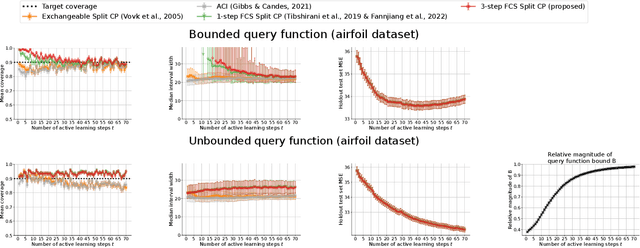
As machine learning (ML) gains widespread adoption, practitioners are increasingly seeking means to quantify and control the risk these systems incur. This challenge is especially salient when ML systems have autonomy to collect their own data, such as in black-box optimization and active learning, where their actions induce sequential feedback-loop shifts in the data distribution. Conformal prediction has emerged as a promising approach to uncertainty and risk quantification, but existing variants either fail to accommodate sequences of data-dependent shifts, or do not fully exploit the fact that agent-induced shift is under our control. In this work we prove that conformal prediction can theoretically be extended to \textit{any} joint data distribution, not just exchangeable or quasi-exchangeable ones, although it is exceedingly impractical to compute in the most general case. For practical applications, we outline a procedure for deriving specific conformal algorithms for any data distribution, and we use this procedure to derive tractable algorithms for a series of agent-induced covariate shifts. We evaluate the proposed algorithms empirically on synthetic black-box optimization and active learning tasks.

Protein Design with Guided Discrete Diffusion

A popular approach to protein design is to combine a generative model with a discriminative model for conditional sampling. The generative model samples plausible sequences while the discriminative model guides a search for sequences with high fitness. Given its broad success in conditional sampling, classifier-guided diffusion modeling is a promising foundation for protein design, leading many to develop guided diffusion models for structure with inverse folding to recover sequences. In this work, we propose diffusioN Optimized Sampling (NOS), a guidance method for discrete diffusion models that follows gradients in the hidden states of the denoising network. NOS makes it possible to perform design directly in sequence space, circumventing significant limitations of structure-based methods, including scarce data and challenging inverse design. Moreover, we use NOS to generalize LaMBO, a Bayesian optimization procedure for sequence design that facilitates multiple objectives and edit-based constraints. The resulting method, LaMBO-2, enables discrete diffusions and stronger performance with limited edits through a novel application of saliency maps. We apply LaMBO-2 to a real-world protein design task, optimizing antibodies for higher expression yield and binding affinity to a therapeutic target under locality and liability constraints, with 97% expression rate and 25% binding rate in exploratory in vitro experiments.

Bayesian Optimization with Conformal Coverage Guarantees

Bayesian optimization is a coherent, ubiquitous approach to decision-making under uncertainty, with applications including multi-arm bandits, active learning, and black-box optimization. Bayesian optimization selects decisions (i.e. objective function queries) with maximal expected utility with respect to the posterior distribution of a Bayesian model, which quantifies reducible, epistemic uncertainty about query outcomes. In practice, subjectively implausible outcomes can occur regularly for two reasons: 1) model misspecification and 2) covariate shift. Conformal prediction is an uncertainty quantification method with coverage guarantees even for misspecified models and a simple mechanism to correct for covariate shift. We propose conformal Bayesian optimization, which directs queries towards regions of search space where the model predictions have guaranteed validity, and investigate its behavior on a suite of black-box optimization tasks and tabular ranking tasks. In many cases we find that query coverage can be significantly improved without harming sample-efficiency.

PropertyDAG: Multi-objective Bayesian optimization of partially ordered, mixed-variable properties for biological sequence design

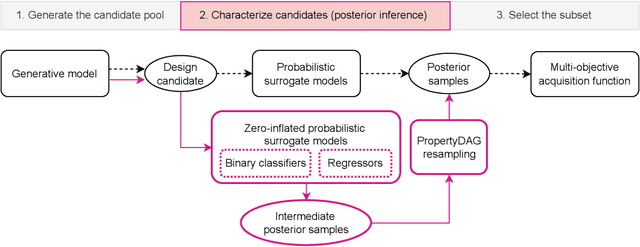
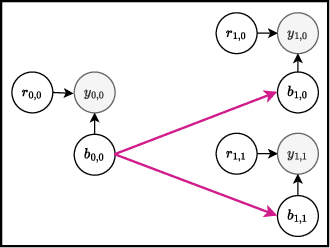
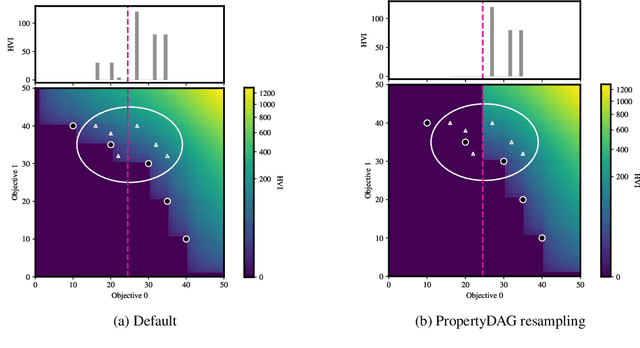
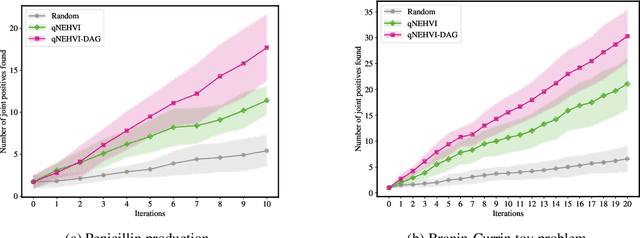
Bayesian optimization offers a sample-efficient framework for navigating the exploration-exploitation trade-off in the vast design space of biological sequences. Whereas it is possible to optimize the various properties of interest jointly using a multi-objective acquisition function, such as the expected hypervolume improvement (EHVI), this approach does not account for objectives with a hierarchical dependency structure. We consider a common use case where some regions of the Pareto frontier are prioritized over others according to a specified $\textit{partial ordering}$ in the objectives. For instance, when designing antibodies, we would like to maximize the binding affinity to a target antigen only if it can be expressed in live cell culture -- modeling the experimental dependency in which affinity can only be measured for antibodies that can be expressed and thus produced in viable quantities. In general, we may want to confer a partial ordering to the properties such that each property is optimized conditioned on its parent properties satisfying some feasibility condition. To this end, we present PropertyDAG, a framework that operates on top of the traditional multi-objective BO to impose this desired ordering on the objectives, e.g. expression $\rightarrow$ affinity. We demonstrate its performance over multiple simulated active learning iterations on a penicillin production task, toy numerical problem, and a real-world antibody design task.

Accelerating Bayesian Optimization for Biological Sequence Design with Denoising Autoencoders

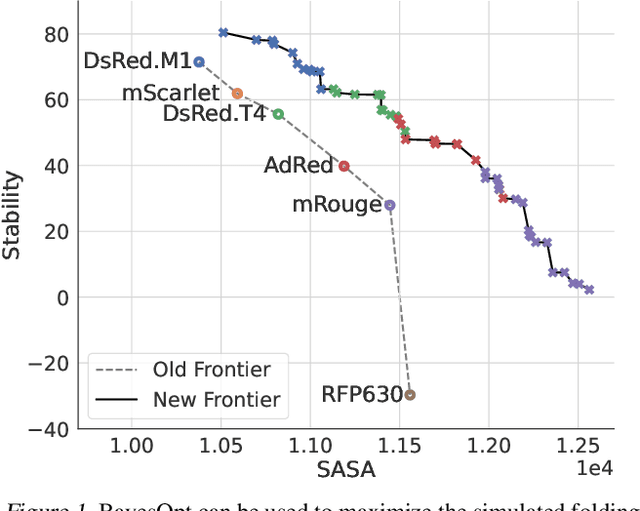
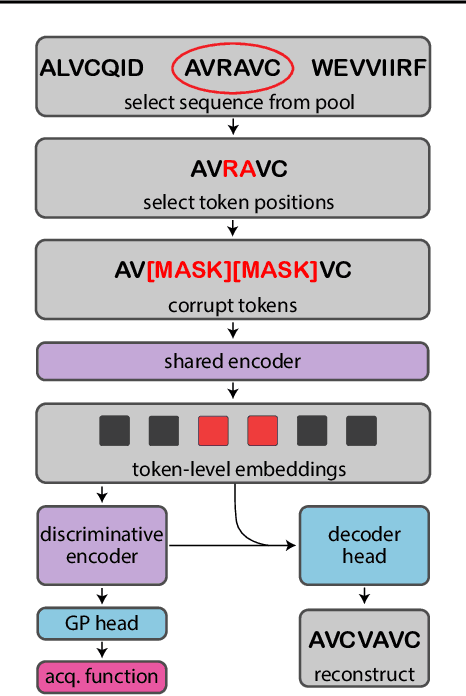
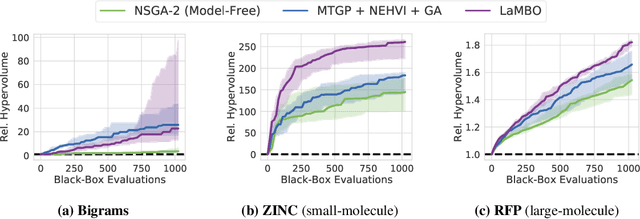
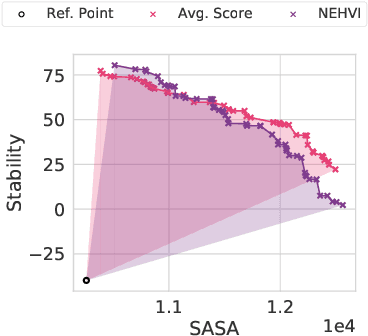
Bayesian optimization is a gold standard for query-efficient continuous optimization. However, its adoption for drug and antibody sequence design has been hindered by the discrete, high-dimensional nature of the decision variables. We develop a new approach (LaMBO) which jointly trains a denoising autoencoder with a discriminative multi-task Gaussian process head, enabling gradient-based optimization of multi-objective acquisition functions in the latent space of the autoencoder. These acquisition functions allow LaMBO to balance the explore-exploit trade-off over multiple design rounds, and to balance objective tradeoffs by optimizing sequences at many different points on the Pareto frontier. We evaluate LaMBO on a small-molecule task based on the ZINC dataset and introduce a new large-molecule task targeting fluorescent proteins. In our experiments, LaMBO outperforms genetic optimizers and does not require a large pretraining corpus, demonstrating that Bayesian optimization is practical and effective for biological sequence design.

Deconstructing the Inductive Biases of Hamiltonian Neural Networks

Physics-inspired neural networks (NNs), such as Hamiltonian or Lagrangian NNs, dramatically outperform other learned dynamics models by leveraging strong inductive biases. These models, however, are challenging to apply to many real world systems, such as those that don't conserve energy or contain contacts, a common setting for robotics and reinforcement learning. In this paper, we examine the inductive biases that make physics-inspired models successful in practice. We show that, contrary to conventional wisdom, the improved generalization of HNNs is the result of modeling acceleration directly and avoiding artificial complexity from the coordinate system, rather than symplectic structure or energy conservation. We show that by relaxing the inductive biases of these models, we can match or exceed performance on energy-conserving systems while dramatically improving performance on practical, non-conservative systems. We extend this approach to constructing transition models for common Mujoco environments, showing that our model can appropriately balance inductive biases with the flexibility required for model-based control.

Conditioning Sparse Variational Gaussian Processes for Online Decision-making

With a principled representation of uncertainty and closed form posterior updates, Gaussian processes (GPs) are a natural choice for online decision making. However, Gaussian processes typically require at least $\mathcal{O}(n^2)$ computations for $n$ training points, limiting their general applicability. Stochastic variational Gaussian processes (SVGPs) can provide scalable inference for a dataset of fixed size, but are difficult to efficiently condition on new data. We propose online variational conditioning (OVC), a procedure for efficiently conditioning SVGPs in an online setting that does not require re-training through the evidence lower bound with the addition of new data. OVC enables the pairing of SVGPs with advanced look-ahead acquisition functions for black-box optimization, even with non-Gaussian likelihoods. We show OVC provides compelling performance in a range of applications including active learning of malaria incidence, and reinforcement learning on MuJoCo simulated robotic control tasks.

Does Knowledge Distillation Really Work?

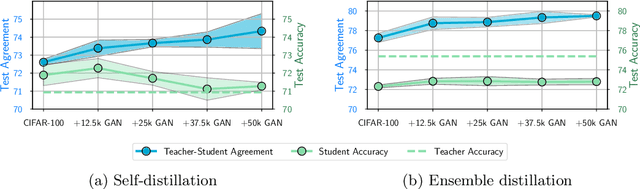
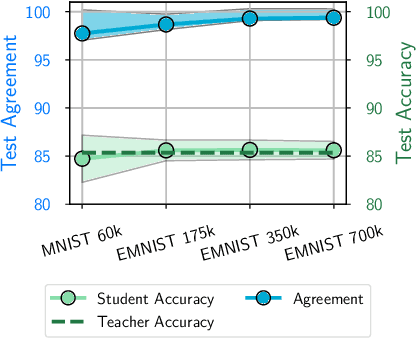
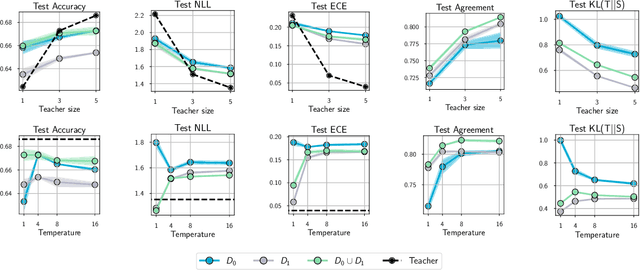
Knowledge distillation is a popular technique for training a small student network to emulate a larger teacher model, such as an ensemble of networks. We show that while knowledge distillation can improve student generalization, it does not typically work as it is commonly understood: there often remains a surprisingly large discrepancy between the predictive distributions of the teacher and the student, even in cases when the student has the capacity to perfectly match the teacher. We identify difficulties in optimization as a key reason for why the student is unable to match the teacher. We also show how the details of the dataset used for distillation play a role in how closely the student matches the teacher -- and that more closely matching the teacher paradoxically does not always lead to better student generalization.