Out-of-Distribution Detection Methods Answer the Wrong Questions

To detect distribution shifts and improve model safety, many out-of-distribution (OOD) detection methods rely on the predictive uncertainty or features of supervised models trained on in-distribution data. In this paper, we critically re-examine this popular family of OOD detection procedures, and we argue that these methods are fundamentally answering the wrong questions for OOD detection. There is no simple fix to this misalignment, since a classifier trained only on in-distribution classes cannot be expected to identify OOD points; for instance, a cat-dog classifier may confidently misclassify an airplane if it contains features that distinguish cats from dogs, despite generally appearing nothing alike. We find that uncertainty-based methods incorrectly conflate high uncertainty with being OOD, while feature-based methods incorrectly conflate far feature-space distance with being OOD. We show how these pathologies manifest as irreducible errors in OOD detection and identify common settings where these methods are ineffective. Additionally, interventions to improve OOD detection such as feature-logit hybrid methods, scaling of model and data size, epistemic uncertainty representation, and outlier exposure also fail to address this fundamental misalignment in objectives. We additionally consider unsupervised density estimation and generative models for OOD detection, which we show have their own fundamental limitations.

MetaFaith: Faithful Natural Language Uncertainty Expression in LLMs

A critical component in the trustworthiness of LLMs is reliable uncertainty communication, yet LLMs often use assertive language when conveying false claims, leading to over-reliance and eroded trust. We present the first systematic study of $\textit{faithful confidence calibration}$ of LLMs, benchmarking models' ability to use linguistic expressions of uncertainty that $\textit{faithfully reflect}$ their intrinsic uncertainty, across a comprehensive array of models, datasets, and prompting strategies. Our results demonstrate that LLMs largely fail at this task, and that existing interventions are insufficient: standard prompt approaches provide only marginal gains, and existing, factuality-based calibration techniques can even harm faithful calibration. To address this critical gap, we introduce MetaFaith, a novel prompt-based calibration approach inspired by human metacognition. We show that MetaFaith robustly improves faithful calibration across diverse models and task domains, enabling up to 61% improvement in faithfulness and achieving an 83% win rate over original generations as judged by humans.

Insertion Language Models: Sequence Generation with Arbitrary-Position Insertions

Autoregressive models (ARMs), which predict subsequent tokens one-by-one ``from left to right,'' have achieved significant success across a wide range of sequence generation tasks. However, they struggle to accurately represent sequences that require satisfying sophisticated constraints or whose sequential dependencies are better addressed by out-of-order generation. Masked Diffusion Models (MDMs) address some of these limitations, but the process of unmasking multiple tokens simultaneously in MDMs can introduce incoherences, and MDMs cannot handle arbitrary infilling constraints when the number of tokens to be filled in is not known in advance. In this work, we introduce Insertion Language Models (ILMs), which learn to insert tokens at arbitrary positions in a sequence -- that is, they select jointly both the position and the vocabulary element to be inserted. By inserting tokens one at a time, ILMs can represent strong dependencies between tokens, and their ability to generate sequences in arbitrary order allows them to accurately model sequences where token dependencies do not follow a left-to-right sequential structure. To train ILMs, we propose a tailored network parameterization and use a simple denoising objective. Our empirical evaluation demonstrates that ILMs outperform both ARMs and MDMs on common planning tasks. Furthermore, we show that ILMs outperform MDMs and perform on par with ARMs in an unconditional text generation task while offering greater flexibility than MDMs in arbitrary-length text infilling.

Learning from Reward-Free Offline Data: A Case for Planning with Latent Dynamics Models

A long-standing goal in AI is to build agents that can solve a variety of tasks across different environments, including previously unseen ones. Two dominant approaches tackle this challenge: (i) reinforcement learning (RL), which learns policies through trial and error, and (ii) optimal control, which plans actions using a learned or known dynamics model. However, their relative strengths and weaknesses remain underexplored in the setting where agents must learn from offline trajectories without reward annotations. In this work, we systematically analyze the performance of different RL and control-based methods under datasets of varying quality. On the RL side, we consider goal-conditioned and zero-shot approaches. On the control side, we train a latent dynamics model using the Joint Embedding Predictive Architecture (JEPA) and use it for planning. We study how dataset properties-such as data diversity, trajectory quality, and environment variability-affect the performance of these approaches. Our results show that model-free RL excels when abundant, high-quality data is available, while model-based planning excels in generalization to novel environment layouts, trajectory stitching, and data-efficiency. Notably, planning with a latent dynamics model emerges as a promising approach for zero-shot generalization from suboptimal data.

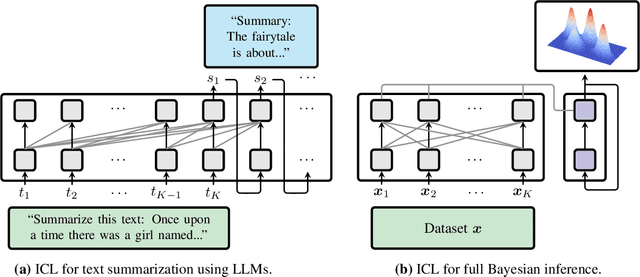
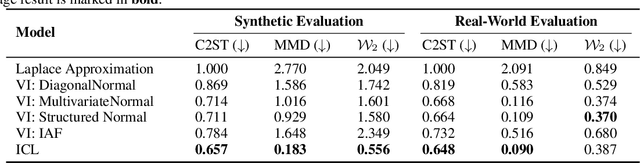
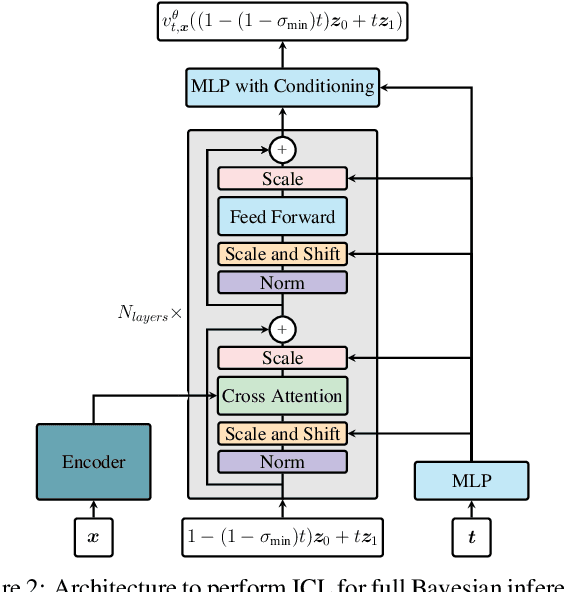
Can Transformers Learn Full Bayesian Inference in Context?

Transformers have emerged as the dominant architecture in the field of deep learning, with a broad range of applications and remarkable in-context learning (ICL) capabilities. While not yet fully understood, ICL has already proved to be an intriguing phenomenon, allowing transformers to learn in context -- without requiring further training. In this paper, we further advance the understanding of ICL by demonstrating that transformers can perform full Bayesian inference for commonly used statistical models in context. More specifically, we introduce a general framework that builds on ideas from prior fitted networks and continuous normalizing flows which enables us to infer complex posterior distributions for methods such as generalized linear models and latent factor models. Extensive experiments on real-world datasets demonstrate that our ICL approach yields posterior samples that are similar in quality to state-of-the-art MCMC or variational inference methods not operating in context.

Improving Pre-Trained Self-Supervised Embeddings Through Effective Entropy Maximization

A number of different architectures and loss functions have been applied to the problem of self-supervised learning (SSL), with the goal of developing embeddings that provide the best possible pre-training for as-yet-unknown, lightly supervised downstream tasks. One of these SSL criteria is to maximize the entropy of a set of embeddings in some compact space. But the goal of maximizing the embedding entropy often depends--whether explicitly or implicitly--upon high dimensional entropy estimates, which typically perform poorly in more than a few dimensions. In this paper, we motivate an effective entropy maximization criterion (E2MC), defined in terms of easy-to-estimate, low-dimensional constraints. We demonstrate that using it to continue training an already-trained SSL model for only a handful of epochs leads to a consistent and, in some cases, significant improvement in downstream performance. We perform careful ablation studies to show that the improved performance is due to the proposed add-on criterion. We also show that continued pre-training with alternative criteria does not lead to notable improvements, and in some cases, even degrades performance.

Exploring the Manifold of Neural Networks Using Diffusion Geometry

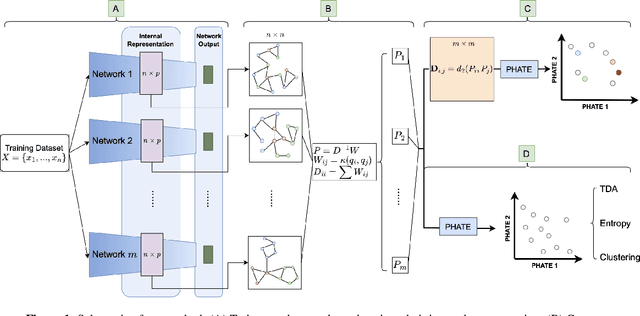
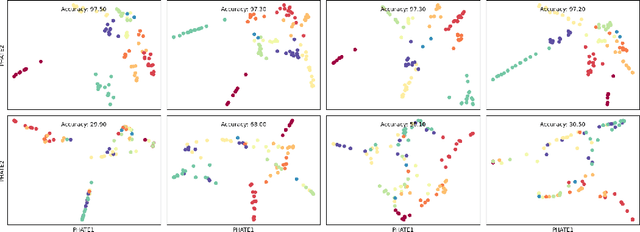
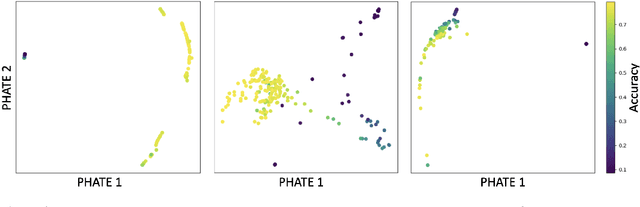
Drawing motivation from the manifold hypothesis, which posits that most high-dimensional data lies on or near low-dimensional manifolds, we apply manifold learning to the space of neural networks. We learn manifolds where datapoints are neural networks by introducing a distance between the hidden layer representations of the neural networks. These distances are then fed to the non-linear dimensionality reduction algorithm PHATE to create a manifold of neural networks. We characterize this manifold using features of the representation, including class separation, hierarchical cluster structure, spectral entropy, and topological structure. Our analysis reveals that high-performing networks cluster together in the manifold, displaying consistent embedding patterns across all these features. Finally, we demonstrate the utility of this approach for guiding hyperparameter optimization and neural architecture search by sampling from the manifold.

A Monte Carlo Framework for Calibrated Uncertainty Estimation in Sequence Prediction

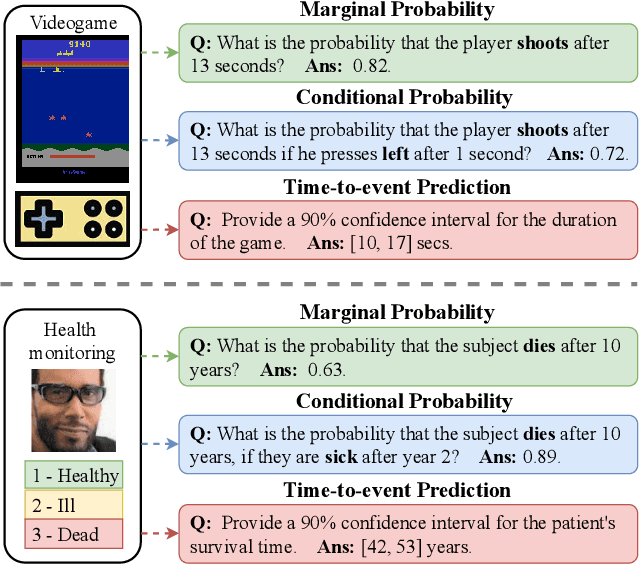
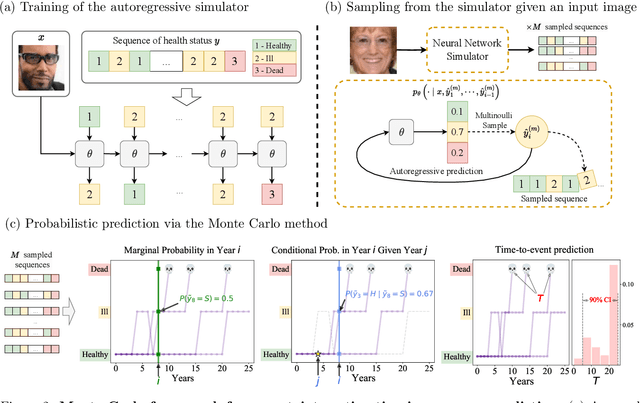
Probabilistic prediction of sequences from images and other high-dimensional data is a key challenge, particularly in risk-sensitive applications. In these settings, it is often desirable to quantify the uncertainty associated with the prediction (instead of just determining the most likely sequence, as in language modeling). In this paper, we propose a Monte Carlo framework to estimate probabilities and confidence intervals associated with the distribution of a discrete sequence. Our framework uses a Monte Carlo simulator, implemented as an autoregressively trained neural network, to sample sequences conditioned on an image input. We then use these samples to estimate the probabilities and confidence intervals. Experiments on synthetic and real data show that the framework produces accurate discriminative predictions, but can suffer from miscalibration. In order to address this shortcoming, we propose a time-dependent regularization method, which is shown to produce calibrated predictions.

Geometry-Aware Generative Autoencoders for Warped Riemannian Metric Learning and Generative Modeling on Data Manifolds

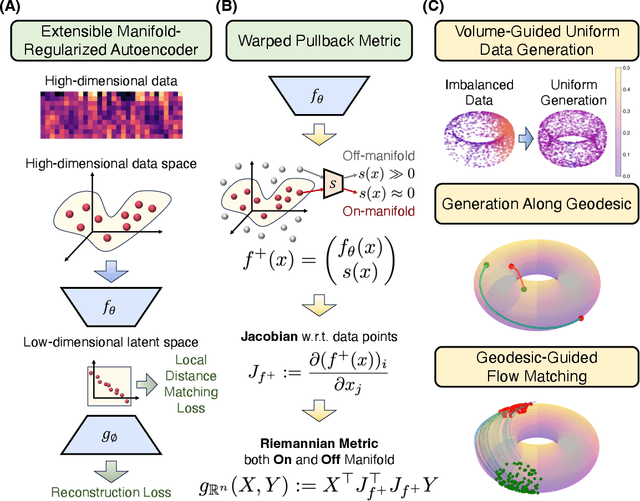
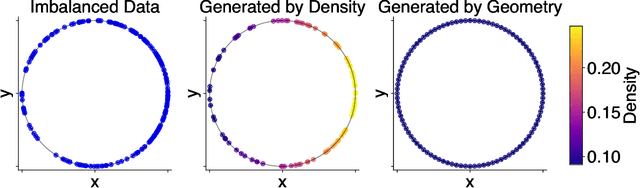
Rapid growth of high-dimensional datasets in fields such as single-cell RNA sequencing and spatial genomics has led to unprecedented opportunities for scientific discovery, but it also presents unique computational and statistical challenges. Traditional methods struggle with geometry-aware data generation, interpolation along meaningful trajectories, and transporting populations via feasible paths. To address these issues, we introduce Geometry-Aware Generative Autoencoder (GAGA), a novel framework that combines extensible manifold learning with generative modeling. GAGA constructs a neural network embedding space that respects the intrinsic geometries discovered by manifold learning and learns a novel warped Riemannian metric on the data space. This warped metric is derived from both the points on the data manifold and negative samples off the manifold, allowing it to characterize a meaningful geometry across the entire latent space. Using this metric, GAGA can uniformly sample points on the manifold, generate points along geodesics, and interpolate between populations across the learned manifold. GAGA shows competitive performance in simulated and real world datasets, including a 30% improvement over the state-of-the-art methods in single-cell population-level trajectory inference.

Context-Guided Diffusion for Out-of-Distribution Molecular and Protein Design

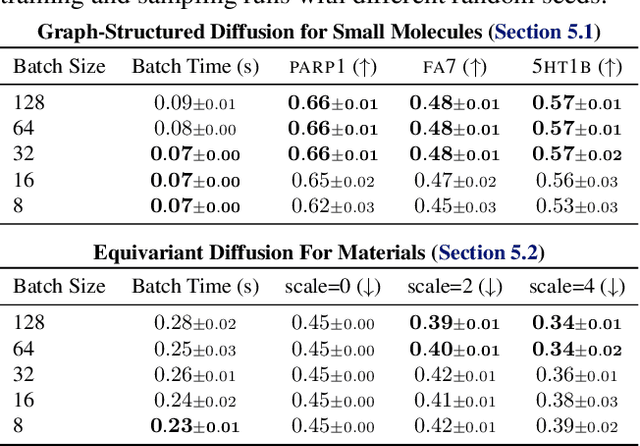
Generative models have the potential to accelerate key steps in the discovery of novel molecular therapeutics and materials. Diffusion models have recently emerged as a powerful approach, excelling at unconditional sample generation and, with data-driven guidance, conditional generation within their training domain. Reliably sampling from high-value regions beyond the training data, however, remains an open challenge -- with current methods predominantly focusing on modifying the diffusion process itself. In this paper, we develop context-guided diffusion (CGD), a simple plug-and-play method that leverages unlabeled data and smoothness constraints to improve the out-of-distribution generalization of guided diffusion models. We demonstrate that this approach leads to substantial performance gains across various settings, including continuous, discrete, and graph-structured diffusion processes with applications across drug discovery, materials science, and protein design.