Dispersion Loss Counteracts Embedding Condensation and Improves Generalization in Small Language Models

Large language models (LLMs) achieve remarkable performance through ever-increasing parameter counts, but scaling incurs steep computational costs. To better understand LLM scaling, we study representational differences between LLMs and their smaller counterparts, with the goal of replicating the representational qualities of larger models in the smaller models. We observe a geometric phenomenon which we term $\textbf{embedding condensation}$, where token embeddings collapse into a narrow cone-like subspace in some language models. Through systematic analyses across multiple Transformer families, we show that small models such as $\texttt{GPT2}$ and $\texttt{Qwen3-0.6B}$ exhibit severe condensation, whereas the larger models such as $\texttt{GPT2-xl}$ and $\texttt{Qwen3-32B}$ are more resistant to this phenomenon. Additional observations show that embedding condensation is not reliably mitigated by knowledge distillation from larger models. To fight against it, we formulate a dispersion loss that explicitly encourages embedding dispersion during training. Experiments demonstrate that it mitigates condensation, recovers dispersion patterns seen in larger models, and yields performance gains across 10 benchmarks. We believe this work offers a principled path toward improving smaller Transformers without additional parameters.

Exploring the Manifold of Neural Networks Using Diffusion Geometry

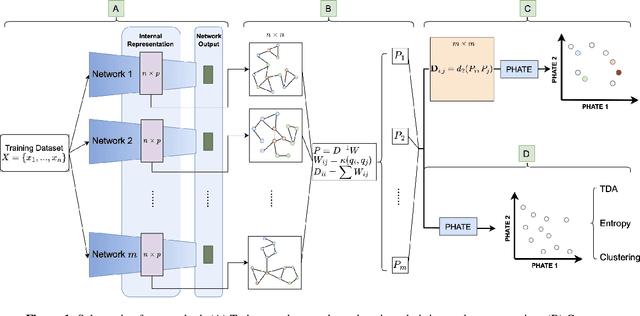
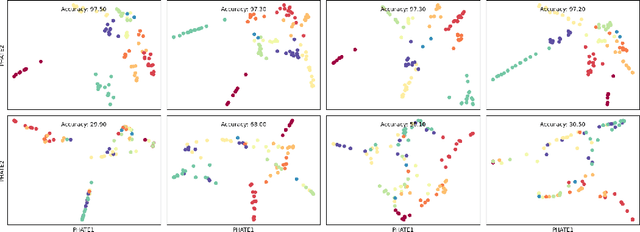
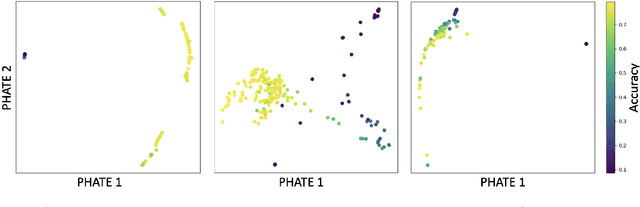
Drawing motivation from the manifold hypothesis, which posits that most high-dimensional data lies on or near low-dimensional manifolds, we apply manifold learning to the space of neural networks. We learn manifolds where datapoints are neural networks by introducing a distance between the hidden layer representations of the neural networks. These distances are then fed to the non-linear dimensionality reduction algorithm PHATE to create a manifold of neural networks. We characterize this manifold using features of the representation, including class separation, hierarchical cluster structure, spectral entropy, and topological structure. Our analysis reveals that high-performing networks cluster together in the manifold, displaying consistent embedding patterns across all these features. Finally, we demonstrate the utility of this approach for guiding hyperparameter optimization and neural architecture search by sampling from the manifold.