Geometry-Aware Generative Autoencoders for Warped Riemannian Metric Learning and Generative Modeling on Data Manifolds

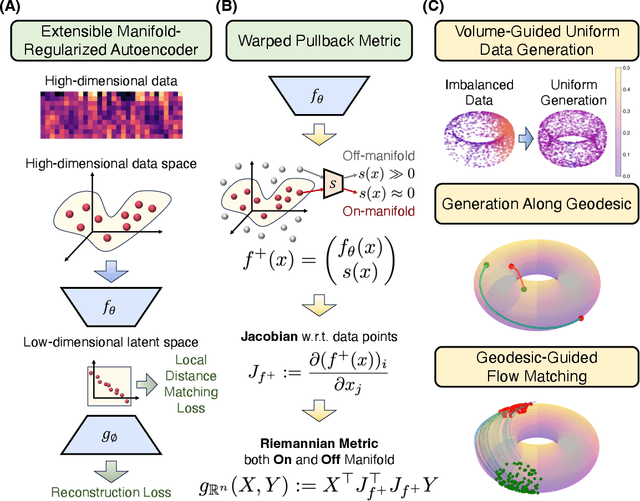
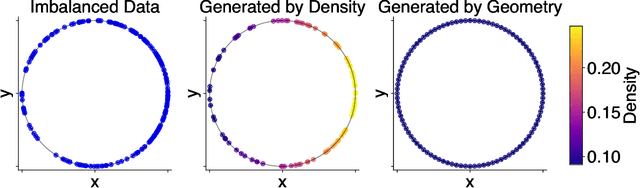
Rapid growth of high-dimensional datasets in fields such as single-cell RNA sequencing and spatial genomics has led to unprecedented opportunities for scientific discovery, but it also presents unique computational and statistical challenges. Traditional methods struggle with geometry-aware data generation, interpolation along meaningful trajectories, and transporting populations via feasible paths. To address these issues, we introduce Geometry-Aware Generative Autoencoder (GAGA), a novel framework that combines extensible manifold learning with generative modeling. GAGA constructs a neural network embedding space that respects the intrinsic geometries discovered by manifold learning and learns a novel warped Riemannian metric on the data space. This warped metric is derived from both the points on the data manifold and negative samples off the manifold, allowing it to characterize a meaningful geometry across the entire latent space. Using this metric, GAGA can uniformly sample points on the manifold, generate points along geodesics, and interpolate between populations across the learned manifold. GAGA shows competitive performance in simulated and real world datasets, including a 30% improvement over the state-of-the-art methods in single-cell population-level trajectory inference.

ImageFlowNet: Forecasting Multiscale Trajectories of Disease Progression with Irregularly-Sampled Longitudinal Medical Images

The forecasting of disease progression from images is a holy grail for clinical decision making. However, this task is complicated by the inherent high dimensionality, temporal sparsity and sampling irregularity in longitudinal image acquisitions. Existing methods often rely on extracting hand-crafted features and performing time-series analysis in this vector space, leading to a loss of rich spatial information within the images. To overcome these challenges, we introduce ImageFlowNet, a novel framework that learns latent-space flow fields that evolve multiscale representations in joint embedding spaces using neural ODEs and SDEs to model disease progression in the image domain. Notably, ImageFlowNet learns multiscale joint representation spaces by combining cohorts of patients together so that information can be transferred between the patient samples. The dynamics then provide plausible trajectories of progression, with the SDE providing alternative trajectories from the same starting point. We provide theoretical insights that support our formulation of ODEs, and motivate our regularizations involving high-level visual features, latent space organization, and trajectory smoothness. We then demonstrate ImageFlowNet's effectiveness through empirical evaluations on three longitudinal medical image datasets depicting progression in retinal geographic atrophy, multiple sclerosis, and glioblastoma.

Sequence-Augmented SE(3)-Flow Matching For Conditional Protein Backbone Generation

Proteins are essential for almost all biological processes and derive their diverse functions from complex 3D structures, which are in turn determined by their amino acid sequences. In this paper, we exploit the rich biological inductive bias of amino acid sequences and introduce FoldFlow-2, a novel sequence-conditioned SE(3)-equivariant flow matching model for protein structure generation. FoldFlow-2 presents substantial new architectural features over the previous FoldFlow family of models including a protein large language model to encode sequence, a new multi-modal fusion trunk that combines structure and sequence representations, and a geometric transformer based decoder. To increase diversity and novelty of generated samples -- crucial for de-novo drug design -- we train FoldFlow-2 at scale on a new dataset that is an order of magnitude larger than PDB datasets of prior works, containing both known proteins in PDB and high-quality synthetic structures achieved through filtering. We further demonstrate the ability to align FoldFlow-2 to arbitrary rewards, e.g. increasing secondary structures diversity, by introducing a Reinforced Finetuning (ReFT) objective. We empirically observe that FoldFlow-2 outperforms previous state-of-the-art protein structure-based generative models, improving over RFDiffusion in terms of unconditional generation across all metrics including designability, diversity, and novelty across all protein lengths, as well as exhibiting generalization on the task of equilibrium conformation sampling. Finally, we demonstrate that a fine-tuned FoldFlow-2 makes progress on challenging conditional design tasks such as designing scaffolds for the VHH nanobody.

Assessing Neural Network Representations During Training Using Noise-Resilient Diffusion Spectral Entropy

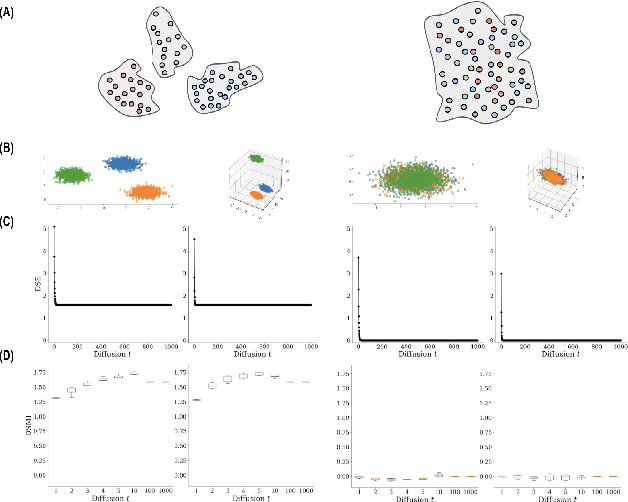
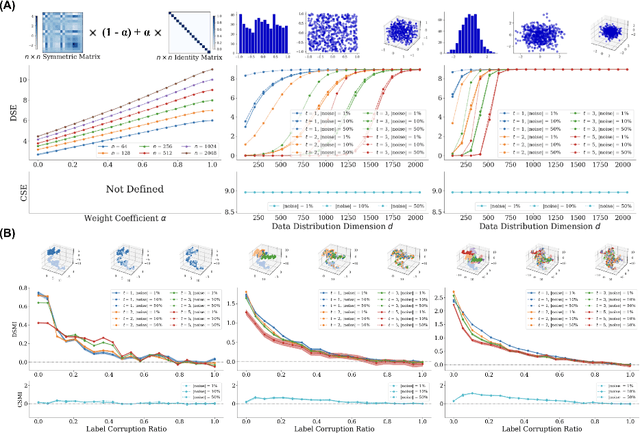
Entropy and mutual information in neural networks provide rich information on the learning process, but they have proven difficult to compute reliably in high dimensions. Indeed, in noisy and high-dimensional data, traditional estimates in ambient dimensions approach a fixed entropy and are prohibitively hard to compute. To address these issues, we leverage data geometry to access the underlying manifold and reliably compute these information-theoretic measures. Specifically, we define diffusion spectral entropy (DSE) in neural representations of a dataset as well as diffusion spectral mutual information (DSMI) between different variables representing data. First, we show that they form noise-resistant measures of intrinsic dimensionality and relationship strength in high-dimensional simulated data that outperform classic Shannon entropy, nonparametric estimation, and mutual information neural estimation (MINE). We then study the evolution of representations in classification networks with supervised learning, self-supervision, or overfitting. We observe that (1) DSE of neural representations increases during training; (2) DSMI with the class label increases during generalizable learning but stays stagnant during overfitting; (3) DSMI with the input signal shows differing trends: on MNIST it increases, while on CIFAR-10 and STL-10 it decreases. Finally, we show that DSE can be used to guide better network initialization and that DSMI can be used to predict downstream classification accuracy across 962 models on ImageNet. The official implementation is available at https://github.com/ChenLiu-1996/DiffusionSpectralEntropy.

SE(3)-Stochastic Flow Matching for Protein Backbone Generation

The computational design of novel protein structures has the potential to impact numerous scientific disciplines greatly. Toward this goal, we introduce $\text{FoldFlow}$ a series of novel generative models of increasing modeling power based on the flow-matching paradigm over $3\text{D}$ rigid motions -- i.e. the group $\text{SE(3)}$ -- enabling accurate modeling of protein backbones. We first introduce $\text{FoldFlow-Base}$, a simulation-free approach to learning deterministic continuous-time dynamics and matching invariant target distributions on $\text{SE(3)}$. We next accelerate training by incorporating Riemannian optimal transport to create $\text{FoldFlow-OT}$, leading to the construction of both more simple and stable flows. Finally, we design $\text{FoldFlow-SFM}$ coupling both Riemannian OT and simulation-free training to learn stochastic continuous-time dynamics over $\text{SE(3)}$. Our family of $\text{FoldFlow}$ generative models offer several key advantages over previous approaches to the generative modeling of proteins: they are more stable and faster to train than diffusion-based approaches, and our models enjoy the ability to map any invariant source distribution to any invariant target distribution over $\text{SE(3)}$. Empirically, we validate our FoldFlow models on protein backbone generation of up to $300$ amino acids leading to high-quality designable, diverse, and novel samples.

Simulation-free Schrödinger bridges via score and flow matching

We present simulation-free score and flow matching ([SF]$^2$M), a simulation-free objective for inferring stochastic dynamics given unpaired source and target samples drawn from arbitrary distributions. Our method generalizes both the score-matching loss used in the training of diffusion models and the recently proposed flow matching loss used in the training of continuous normalizing flows. [SF]$^2$M interprets continuous-time stochastic generative modeling as a Schr\"odinger bridge (SB) problem. It relies on static entropy-regularized optimal transport, or a minibatch approximation, to efficiently learn the SB without simulating the learned stochastic process. We find that [SF]$^2$M is more efficient and gives more accurate solutions to the SB problem than simulation-based methods from prior work. Finally, we apply [SF]$^2$M to the problem of learning cell dynamics from snapshot data. Notably, [SF]$^2$M is the first method to accurately model cell dynamics in high dimensions and can recover known gene regulatory networks from simulated data.

Neural FIM for learning Fisher Information Metrics from point cloud data

Although data diffusion embeddings are ubiquitous in unsupervised learning and have proven to be a viable technique for uncovering the underlying intrinsic geometry of data, diffusion embeddings are inherently limited due to their discrete nature. To this end, we propose neural FIM, a method for computing the Fisher information metric (FIM) from point cloud data - allowing for a continuous manifold model for the data. Neural FIM creates an extensible metric space from discrete point cloud data such that information from the metric can inform us of manifold characteristics such as volume and geodesics. We demonstrate Neural FIM's utility in selecting parameters for the PHATE visualization method as well as its ability to obtain information pertaining to local volume illuminating branching points and cluster centers embeddings of a toy dataset and two single-cell datasets of IPSC reprogramming and PBMCs (immune cells).

Graph Fourier MMD for Signals on Graphs

While numerous methods have been proposed for computing distances between probability distributions in Euclidean space, relatively little attention has been given to computing such distances for distributions on graphs. However, there has been a marked increase in data that either lies on graph (such as protein interaction networks) or can be modeled as a graph (single cell data), particularly in the biomedical sciences. Thus, it becomes important to find ways to compare signals defined on such graphs. Here, we propose Graph Fourier MMD (GFMMD), a novel distance between distributions and signals on graphs. GFMMD is defined via an optimal witness function that is both smooth on the graph and maximizes difference in expectation between the pair of distributions on the graph. We find an analytical solution to this optimization problem as well as an embedding of distributions that results from this method. We also prove several properties of this method including scale invariance and applicability to disconnected graphs. We showcase it on graph benchmark datasets as well on single cell RNA-sequencing data analysis. In the latter, we use the GFMMD-based gene embeddings to find meaningful gene clusters. We also propose a novel type of score for gene selection called "gene localization score" which helps select genes for cellular state space characterization.

A Heat Diffusion Perspective on Geodesic Preserving Dimensionality Reduction

Diffusion-based manifold learning methods have proven useful in representation learning and dimensionality reduction of modern high dimensional, high throughput, noisy datasets. Such datasets are especially present in fields like biology and physics. While it is thought that these methods preserve underlying manifold structure of data by learning a proxy for geodesic distances, no specific theoretical links have been established. Here, we establish such a link via results in Riemannian geometry explicitly connecting heat diffusion to manifold distances. In this process, we also formulate a more general heat kernel based manifold embedding method that we call heat geodesic embeddings. This novel perspective makes clearer the choices available in manifold learning and denoising. Results show that our method outperforms existing state of the art in preserving ground truth manifold distances, and preserving cluster structure in toy datasets. We also showcase our method on single cell RNA-sequencing datasets with both continuum and cluster structure, where our method enables interpolation of withheld timepoints of data. Finally, we show that parameters of our more general method can be configured to give results similar to PHATE (a state-of-the-art diffusion based manifold learning method) as well as SNE (an attraction/repulsion neighborhood based method that forms the basis of t-SNE).

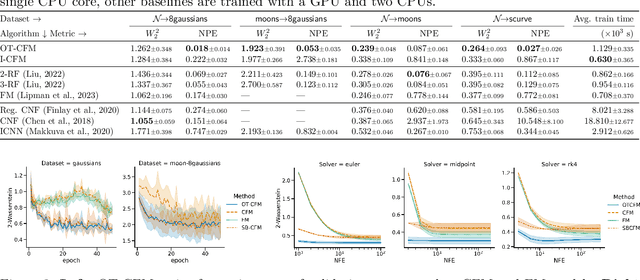
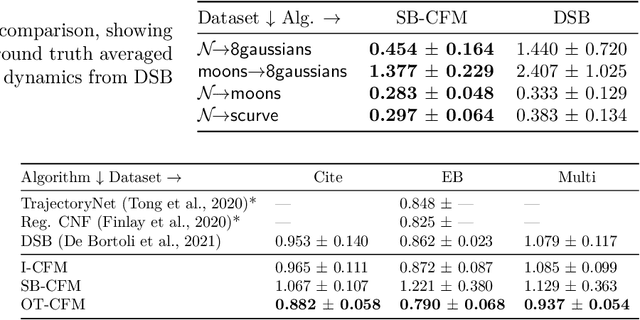
Conditional Flow Matching: Simulation-Free Dynamic Optimal Transport

Continuous normalizing flows (CNFs) are an attractive generative modeling technique, but they have thus far been held back by limitations in their simulation-based maximum likelihood training. In this paper, we introduce a new technique called conditional flow matching (CFM), a simulation-free training objective for CNFs. CFM features a stable regression objective like that used to train the stochastic flow in diffusion models but enjoys the efficient inference of deterministic flow models. In contrast to both diffusion models and prior CNF training algorithms, our CFM objective does not require the source distribution to be Gaussian or require evaluation of its density. Based on this new objective, we also introduce optimal transport CFM (OT-CFM), which creates simpler flows that are more stable to train and lead to faster inference, as evaluated in our experiments. Training CNFs with CFM improves results on a variety of conditional and unconditional generation tasks such as inferring single cell dynamics, unsupervised image translation, and Schr\"odinger bridge inference. Code is available at https://github.com/atong01/conditional-flow-matching .