Graph topological property recovery with heat and wave dynamics-based features on graphs

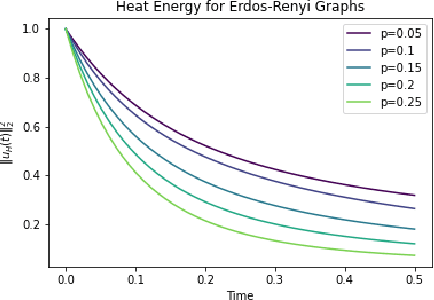
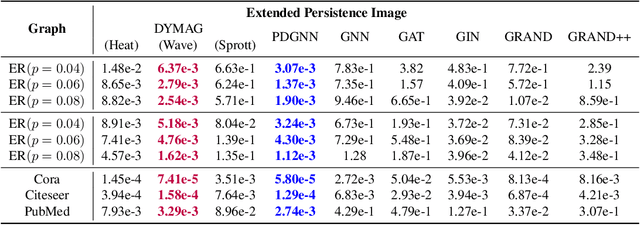
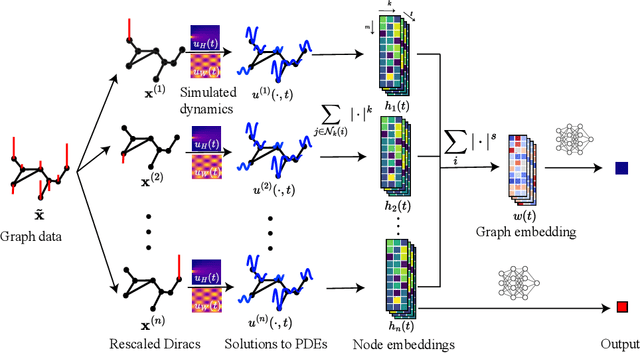
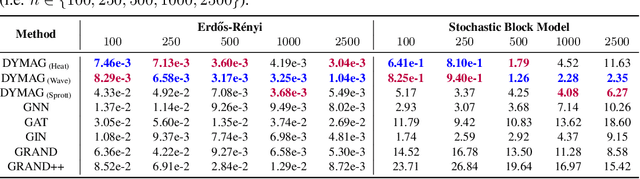
In this paper, we propose Graph Differential Equation Network (GDeNet), an approach that harnesses the expressive power of solutions to PDEs on a graph to obtain continuous node- and graph-level representations for various downstream tasks. We derive theoretical results connecting the dynamics of heat and wave equations to the spectral properties of the graph and to the behavior of continuous-time random walks on graphs. We demonstrate experimentally that these dynamics are able to capture salient aspects of graph geometry and topology by recovering generating parameters of random graphs, Ricci curvature, and persistent homology. Furthermore, we demonstrate the superior performance of GDeNet on real-world datasets including citation graphs, drug-like molecules, and proteins.

Neural FIM for learning Fisher Information Metrics from point cloud data

Although data diffusion embeddings are ubiquitous in unsupervised learning and have proven to be a viable technique for uncovering the underlying intrinsic geometry of data, diffusion embeddings are inherently limited due to their discrete nature. To this end, we propose neural FIM, a method for computing the Fisher information metric (FIM) from point cloud data - allowing for a continuous manifold model for the data. Neural FIM creates an extensible metric space from discrete point cloud data such that information from the metric can inform us of manifold characteristics such as volume and geodesics. We demonstrate Neural FIM's utility in selecting parameters for the PHATE visualization method as well as its ability to obtain information pertaining to local volume illuminating branching points and cluster centers embeddings of a toy dataset and two single-cell datasets of IPSC reprogramming and PBMCs (immune cells).

Manifold Interpolating Optimal-Transport Flows for Trajectory Inference

Here, we present a method called Manifold Interpolating Optimal-Transport Flow (MIOFlow) that learns stochastic, continuous population dynamics from static snapshot samples taken at sporadic timepoints. MIOFlow combines dynamic models, manifold learning, and optimal transport by training neural ordinary differential equations (Neural ODE) to interpolate between static population snapshots as penalized by optimal transport with manifold ground distance. Further, we ensure that the flow follows the geometry by operating in the latent space of an autoencoder that we call a geodesic autoencoder (GAE). In GAE the latent space distance between points is regularized to match a novel multiscale geodesic distance on the data manifold that we define. We show that this method is superior to normalizing flows, Schr\"odinger bridges and other generative models that are designed to flow from noise to data in terms of interpolating between populations. Theoretically, we link these trajectories with dynamic optimal transport. We evaluate our method on simulated data with bifurcations and merges, as well as scRNA-seq data from embryoid body differentiation, and acute myeloid leukemia treatment.

Diffusion Curvature for Estimating Local Curvature in High Dimensional Data

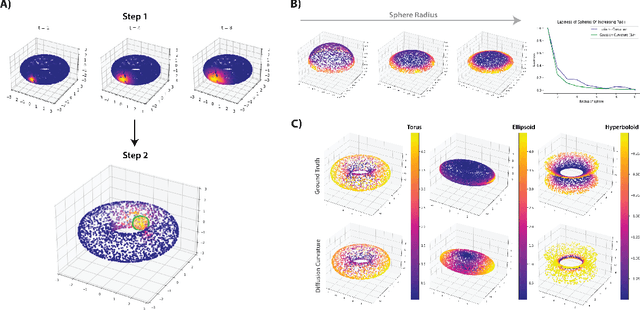
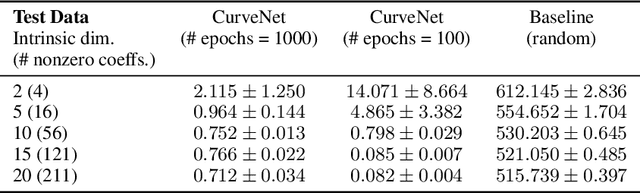
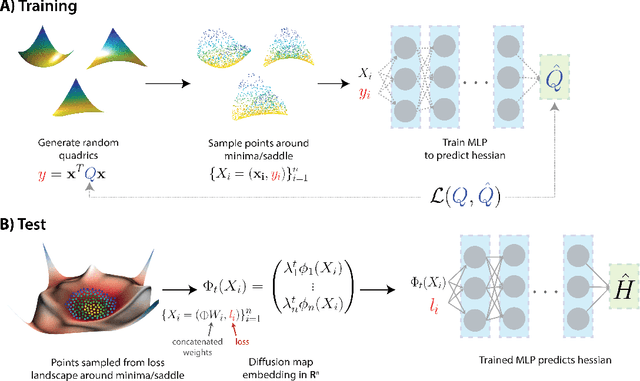
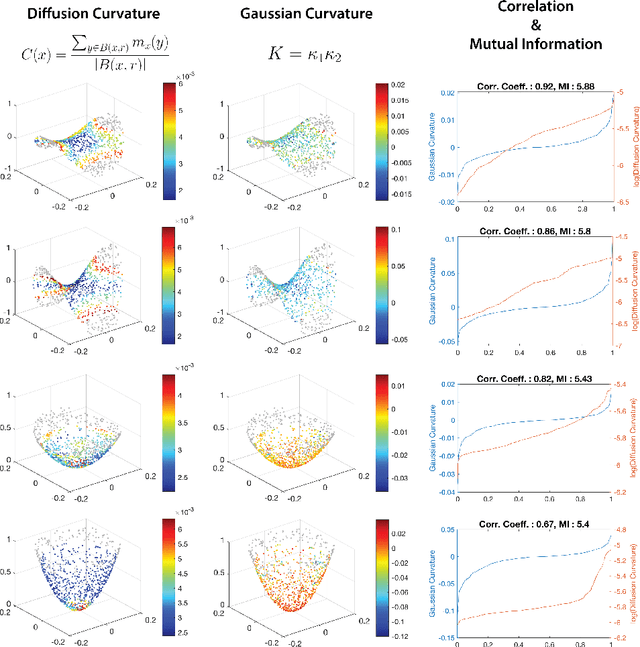
We introduce a new intrinsic measure of local curvature on point-cloud data called diffusion curvature. Our measure uses the framework of diffusion maps, including the data diffusion operator, to structure point cloud data and define local curvature based on the laziness of a random walk starting at a point or region of the data. We show that this laziness directly relates to volume comparison results from Riemannian geometry. We then extend this scalar curvature notion to an entire quadratic form using neural network estimations based on the diffusion map of point-cloud data. We show applications of both estimations on toy data, single-cell data, and on estimating local Hessian matrices of neural network loss landscapes.