Geometry-Aware Edge Pooling for Graph Neural Networks

Graph Neural Networks (GNNs) have shown significant success for graph-based tasks. Motivated by the prevalence of large datasets in real-world applications, pooling layers are crucial components of GNNs. By reducing the size of input graphs, pooling enables faster training and potentially better generalisation. However, existing pooling operations often optimise for the learning task at the expense of fundamental graph structures and interpretability. This leads to unreliable performance across varying dataset types, downstream tasks and pooling ratios. Addressing these concerns, we propose novel graph pooling layers for structure aware pooling via edge collapses. Our methods leverage diffusion geometry and iteratively reduce a graph's size while preserving both its metric structure and structural diversity. We guide pooling using magnitude, an isometry-invariant diversity measure, which permits us to control the fidelity of the pooling process. Further, we use the spread of a metric space as a faster and more stable alternative ensuring computational efficiency. Empirical results demonstrate that our methods (i) achieve superior performance compared to alternative pooling layers across a range of diverse graph classification tasks, (ii) preserve key spectral properties of the input graphs, and (iii) retain high accuracy across varying pooling ratios.

RETRO SYNFLOW: Discrete Flow Matching for Accurate and Diverse Single-Step Retrosynthesis

A fundamental problem in organic chemistry is identifying and predicting the series of reactions that synthesize a desired target product molecule. Due to the combinatorial nature of the chemical search space, single-step reactant prediction -- i.e. single-step retrosynthesis -- remains challenging even for existing state-of-the-art template-free generative approaches to produce an accurate yet diverse set of feasible reactions. In this paper, we model single-step retrosynthesis planning and introduce RETRO SYNFLOW (RSF) a discrete flow-matching framework that builds a Markov bridge between the prescribed target product molecule and the reactant molecule. In contrast to past approaches, RSF employs a reaction center identification step to produce intermediate structures known as synthons as a more informative source distribution for the discrete flow. To further enhance diversity and feasibility of generated samples, we employ Feynman-Kac steering with Sequential Monte Carlo based resampling to steer promising generations at inference using a new reward oracle that relies on a forward-synthesis model. Empirically, we demonstrate \nameshort achieves $60.0 \%$ top-1 accuracy, which outperforms the previous SOTA by $20 \%$. We also substantiate the benefits of steering at inference and demonstrate that FK-steering improves top-$5$ round-trip accuracy by $19 \%$ over prior template-free SOTA methods, all while preserving competitive top-$k$ accuracy results.

Random Forest Autoencoders for Guided Representation Learning

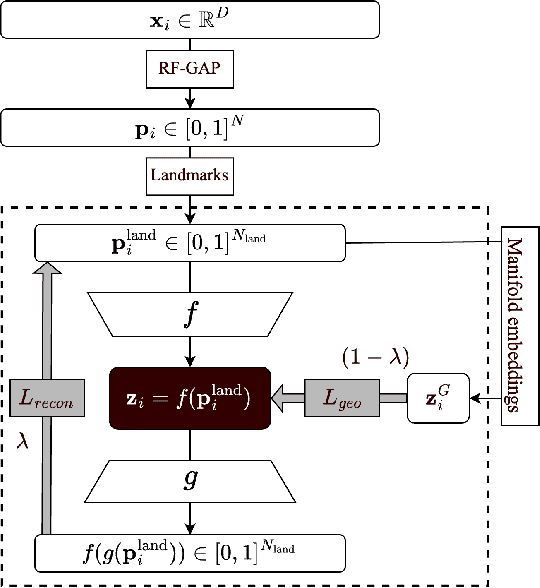
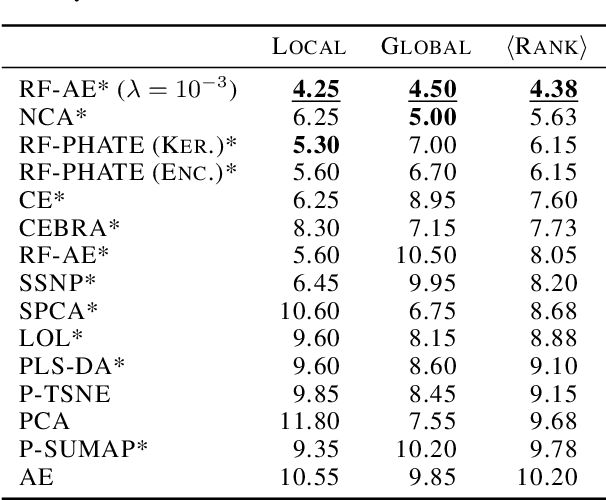
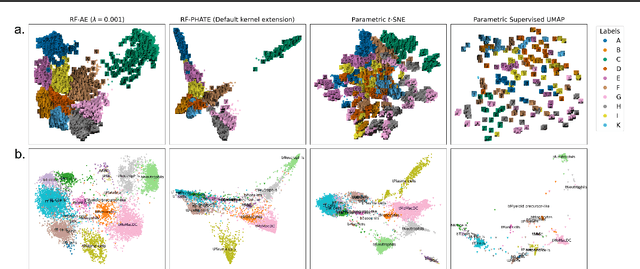
Decades of research have produced robust methods for unsupervised data visualization, yet supervised visualization$\unicode{x2013}$where expert labels guide representations$\unicode{x2013}$remains underexplored, as most supervised approaches prioritize classification over visualization. Recently, RF-PHATE, a diffusion-based manifold learning method leveraging random forests and information geometry, marked significant progress in supervised visualization. However, its lack of an explicit mapping function limits scalability and prevents application to unseen data, posing challenges for large datasets and label-scarce scenarios. To overcome these limitations, we introduce Random Forest Autoencoders (RF-AE), a neural network-based framework for out-of-sample kernel extension that combines the flexibility of autoencoders with the supervised learning strengths of random forests and the geometry captured by RF-PHATE. RF-AE enables efficient out-of-sample supervised visualization and outperforms existing methods, including RF-PHATE's standard kernel extension, in both accuracy and interpretability. Additionally, RF-AE is robust to the choice of hyper-parameters and generalizes to any kernel-based dimensionality reduction method.

Principal Curvatures Estimation with Applications to Single Cell Data

The rapidly growing field of single-cell transcriptomic sequencing (scRNAseq) presents challenges for data analysis due to its massive datasets. A common method in manifold learning consists in hypothesizing that datasets lie on a lower dimensional manifold. This allows to study the geometry of point clouds by extracting meaningful descriptors like curvature. In this work, we will present Adaptive Local PCA (AdaL-PCA), a data-driven method for accurately estimating various notions of intrinsic curvature on data manifolds, in particular principal curvatures for surfaces. The model relies on local PCA to estimate the tangent spaces. The evaluation of AdaL-PCA on sampled surfaces shows state-of-the-art results. Combined with a PHATE embedding, the model applied to single-cell RNA sequencing data allows us to identify key variations in the cellular differentiation.

Non-Uniform Parameter-Wise Model Merging

Combining multiple machine learning models has long been a technique for enhancing performance, particularly in distributed settings. Traditional approaches, such as model ensembles, work well, but are expensive in terms of memory and compute. Recently, methods based on averaging model parameters have achieved good results in some settings and have gained popularity. However, merging models initialized differently that do not share a part of their training trajectories can yield worse results than simply using the base models, even after aligning their neurons. In this paper, we introduce a novel approach, Non-uniform Parameter-wise Model Merging, or NP Merge, which merges models by learning the contribution of each parameter to the final model using gradient-based optimization. We empirically demonstrate the effectiveness of our method for merging models of various architectures in multiple settings, outperforming past methods. We also extend NP Merge to handle the merging of multiple models, showcasing its scalability and robustness.

Towards Graph Foundation Models: A Study on the Generalization of Positional and Structural Encodings

Recent advances in integrating positional and structural encodings (PSEs) into graph neural networks (GNNs) have significantly enhanced their performance across various graph learning tasks. However, the general applicability of these encodings and their potential to serve as foundational representations for graphs remain uncertain. This paper investigates the fine-tuning efficiency, scalability with sample size, and generalization capability of learnable PSEs across diverse graph datasets. Specifically, we evaluate their potential as universal pre-trained models that can be easily adapted to new tasks with minimal fine-tuning and limited data. Furthermore, we assess the expressivity of the learned representations, particularly, when used to augment downstream GNNs. We demonstrate through extensive benchmarking and empirical analysis that PSEs generally enhance downstream models. However, some datasets may require specific PSE-augmentations to achieve optimal performance. Nevertheless, our findings highlight their significant potential to become integral components of future graph foundation models. We provide new insights into the strengths and limitations of PSEs, contributing to the broader discourse on foundation models in graph learning.

Reaction-conditioned De Novo Enzyme Design with GENzyme

The introduction of models like RFDiffusionAA, AlphaFold3, AlphaProteo, and Chai1 has revolutionized protein structure modeling and interaction prediction, primarily from a binding perspective, focusing on creating ideal lock-and-key models. However, these methods can fall short for enzyme-substrate interactions, where perfect binding models are rare, and induced fit states are more common. To address this, we shift to a functional perspective for enzyme design, where the enzyme function is defined by the reaction it catalyzes. Here, we introduce \textsc{GENzyme}, a \textit{de novo} enzyme design model that takes a catalytic reaction as input and generates the catalytic pocket, full enzyme structure, and enzyme-substrate binding complex. \textsc{GENzyme} is an end-to-end, three-staged model that integrates (1) a catalytic pocket generation and sequence co-design module, (2) a pocket inpainting and enzyme inverse folding module, and (3) a binding and screening module to optimize and predict enzyme-substrate complexes. The entire design process is driven by the catalytic reaction being targeted. This reaction-first approach allows for more accurate and biologically relevant enzyme design, potentially surpassing structure-based and binding-focused models in creating enzymes capable of catalyzing specific reactions. We provide \textsc{GENzyme} code at https://github.com/WillHua127/GENzyme.

Geometry-Aware Generative Autoencoders for Warped Riemannian Metric Learning and Generative Modeling on Data Manifolds

Rapid growth of high-dimensional datasets in fields such as single-cell RNA sequencing and spatial genomics has led to unprecedented opportunities for scientific discovery, but it also presents unique computational and statistical challenges. Traditional methods struggle with geometry-aware data generation, interpolation along meaningful trajectories, and transporting populations via feasible paths. To address these issues, we introduce Geometry-Aware Generative Autoencoder (GAGA), a novel framework that combines extensible manifold learning with generative modeling. GAGA constructs a neural network embedding space that respects the intrinsic geometries discovered by manifold learning and learns a novel warped Riemannian metric on the data space. This warped metric is derived from both the points on the data manifold and negative samples off the manifold, allowing it to characterize a meaningful geometry across the entire latent space. Using this metric, GAGA can uniformly sample points on the manifold, generate points along geodesics, and interpolate between populations across the learned manifold. GAGA shows competitive performance in simulated and real world datasets, including a 30% improvement over the state-of-the-art methods in single-cell population-level trajectory inference.

Are Heterophily-Specific GNNs and Homophily Metrics Really Effective? Evaluation Pitfalls and New Benchmarks

Over the past decade, Graph Neural Networks (GNNs) have achieved great success on machine learning tasks with relational data. However, recent studies have found that heterophily can cause significant performance degradation of GNNs, especially on node-level tasks. Numerous heterophilic benchmark datasets have been put forward to validate the efficacy of heterophily-specific GNNs and various homophily metrics have been designed to help people recognize these malignant datasets. Nevertheless, there still exist multiple pitfalls that severely hinder the proper evaluation of new models and metrics. In this paper, we point out three most serious pitfalls: 1) a lack of hyperparameter tuning; 2) insufficient model evaluation on the real challenging heterophilic datasets; 3) missing quantitative evaluation benchmark for homophily metrics on synthetic graphs. To overcome these challenges, we first train and fine-tune baseline models on $27$ most widely used benchmark datasets, categorize them into three distinct groups: malignant, benign and ambiguous heterophilic datasets, and identify the real challenging subsets of tasks. To our best knowledge, we are the first to propose such taxonomy. Then, we re-evaluate $10$ heterophily-specific state-of-the-arts (SOTA) GNNs with fine-tuned hyperparameters on different groups of heterophilic datasets. Based on the model performance, we reassess their effectiveness on addressing heterophily challenge. At last, we evaluate $11$ popular homophily metrics on synthetic graphs with three different generation approaches. To compare the metrics strictly, we propose the first quantitative evaluation method based on Fr\'echet distance.

Reactzyme: A Benchmark for Enzyme-Reaction Prediction

Enzymes, with their specific catalyzed reactions, are necessary for all aspects of life, enabling diverse biological processes and adaptations. Predicting enzyme functions is essential for understanding biological pathways, guiding drug development, enhancing bioproduct yields, and facilitating evolutionary studies. Addressing the inherent complexities, we introduce a new approach to annotating enzymes based on their catalyzed reactions. This method provides detailed insights into specific reactions and is adaptable to newly discovered reactions, diverging from traditional classifications by protein family or expert-derived reaction classes. We employ machine learning algorithms to analyze enzyme reaction datasets, delivering a much more refined view on the functionality of enzymes. Our evaluation leverages the largest enzyme-reaction dataset to date, derived from the SwissProt and Rhea databases with entries up to January 8, 2024. We frame the enzyme-reaction prediction as a retrieval problem, aiming to rank enzymes by their catalytic ability for specific reactions. With our model, we can recruit proteins for novel reactions and predict reactions in novel proteins, facilitating enzyme discovery and function annotation.