Forest-Guided Semantic Transport for Label-Supervised Manifold Alignment

Label-supervised manifold alignment bridges the gap between unsupervised and correspondence-based paradigms by leveraging shared label information to align multimodal datasets. Still, most existing methods rely on Euclidean geometry to model intra-domain relationships. This approach can fail when features are only weakly related to the task of interest, leading to noisy, semantically misleading structure and degraded alignment quality. To address this limitation, we introduce FoSTA (Forest-guided Semantic Transport Alignment), a scalable alignment framework that leverages forest-induced geometry to denoise intra-domain structure and recover task-relevant manifolds prior to alignment. FoSTA builds semantic representations directly from label-informed forest affinities and aligns them via fast, hierarchical semantic transport, capturing meaningful cross-domain relationships. Extensive comparisons with established baselines demonstrate that FoSTA improves correspondence recovery and label transfer on synthetic benchmarks and delivers strong performance in practical single-cell applications, including batch correction and biological conservation.

Scalable Tree Ensemble Proximities in Python

Tree ensemble methods such as Random Forests naturally induce supervised similarity measures through their decision tree structure, but existing implementations of proximities derived from tree ensembles typically suffer from quadratic time or memory complexity, limiting their scalability. In this work, we introduce a general framework for efficient proximity computation by defining a family of Separable Weighted Leaf-Collision Proximities. We show that any proximity measure in this family admits an exact sparse matrix factorization, restricting computation to leaf-level collisions and avoiding explicit pairwise comparisons. This formulation enables low-memory, scalable proximity computation using sparse linear algebra in Python. Empirical benchmarks demonstrate substantial runtime and memory improvements over traditional approaches, allowing tree ensemble proximities to scale efficiently to datasets with hundreds of thousands of samples on standard CPU hardware.

Random Forest Autoencoders for Guided Representation Learning

Decades of research have produced robust methods for unsupervised data visualization, yet supervised visualization$\unicode{x2013}$where expert labels guide representations$\unicode{x2013}$remains underexplored, as most supervised approaches prioritize classification over visualization. Recently, RF-PHATE, a diffusion-based manifold learning method leveraging random forests and information geometry, marked significant progress in supervised visualization. However, its lack of an explicit mapping function limits scalability and prevents application to unseen data, posing challenges for large datasets and label-scarce scenarios. To overcome these limitations, we introduce Random Forest Autoencoders (RF-AE), a neural network-based framework for out-of-sample kernel extension that combines the flexibility of autoencoders with the supervised learning strengths of random forests and the geometry captured by RF-PHATE. RF-AE enables efficient out-of-sample supervised visualization and outperforms existing methods, including RF-PHATE's standard kernel extension, in both accuracy and interpretability. Additionally, RF-AE is robust to the choice of hyper-parameters and generalizes to any kernel-based dimensionality reduction method.

Random Forest-Supervised Manifold Alignment

Manifold alignment is a type of data fusion technique that creates a shared low-dimensional representation of data collected from multiple domains, enabling cross-domain learning and improved performance in downstream tasks. This paper presents an approach to manifold alignment using random forests as a foundation for semi-supervised alignment algorithms, leveraging the model's inherent strengths. We focus on enhancing two recently developed alignment graph-based by integrating class labels through geometry-preserving proximities derived from random forests. These proximities serve as a supervised initialization for constructing cross-domain relationships that maintain local neighborhood structures, thereby facilitating alignment. Our approach addresses a common limitation in manifold alignment, where existing methods often fail to generate embeddings that capture sufficient information for downstream classification. By contrast, we find that alignment models that use random forest proximities or class-label information achieve improved accuracy on downstream classification tasks, outperforming single-domain baselines. Experiments across multiple datasets show that our method typically enhances cross-domain feature integration and predictive performance, suggesting that random forest proximities offer a practical solution for tasks requiring multimodal data alignment.

Graph Integration for Diffusion-Based Manifold Alignment

Data from individual observations can originate from various sources or modalities but are often intrinsically linked. Multimodal data integration can enrich information content compared to single-source data. Manifold alignment is a form of data integration that seeks a shared, underlying low-dimensional representation of multiple data sources that emphasizes similarities between alternative representations of the same entities. Semi-supervised manifold alignment relies on partially known correspondences between domains, either through shared features or through other known associations. In this paper, we introduce two semi-supervised manifold alignment methods. The first method, Shortest Paths on the Union of Domains (SPUD), forms a unified graph structure using known correspondences to establish graph edges. By learning inter-domain geodesic distances, SPUD creates a global, multi-domain structure. The second method, MASH (Manifold Alignment via Stochastic Hopping), learns local geometry within each domain and forms a joint diffusion operator using known correspondences to iteratively learn new inter-domain correspondences through a random-walk approach. Through the diffusion process, MASH forms a coupling matrix that links heterogeneous domains into a unified structure. We compare SPUD and MASH with existing semi-supervised manifold alignment methods and show that they outperform competing methods in aligning true correspondences and cross-domain classification. In addition, we show how these methods can be applied to transfer label information between domains.

Enhancing Supervised Visualization through Autoencoder and Random Forest Proximities for Out-of-Sample Extension

The value of supervised dimensionality reduction lies in its ability to uncover meaningful connections between data features and labels. Common dimensionality reduction methods embed a set of fixed, latent points, but are not capable of generalizing to an unseen test set. In this paper, we provide an out-of-sample extension method for the random forest-based supervised dimensionality reduction method, RF-PHATE, combining information learned from the random forest model with the function-learning capabilities of autoencoders. Through quantitative assessment of various autoencoder architectures, we identify that networks that reconstruct random forest proximities are more robust for the embedding extension problem. Furthermore, by leveraging proximity-based prototypes, we achieve a 40% reduction in training time without compromising extension quality. Our method does not require label information for out-of-sample points, thus serving as a semi-supervised method, and can achieve consistent quality using only 10% of the training data.

Supervised Manifold Learning via Random Forest Geometry-Preserving Proximities

Manifold learning approaches seek the intrinsic, low-dimensional data structure within a high-dimensional space. Mainstream manifold learning algorithms, such as Isomap, UMAP, $t$-SNE, Diffusion Map, and Laplacian Eigenmaps do not use data labels and are thus considered unsupervised. Existing supervised extensions of these methods are limited to classification problems and fall short of uncovering meaningful embeddings due to their construction using order non-preserving, class-conditional distances. In this paper, we show the weaknesses of class-conditional manifold learning quantitatively and visually and propose an alternate choice of kernel for supervised dimensionality reduction using a data-geometry-preserving variant of random forest proximities as an initialization for manifold learning methods. We show that local structure preservation using these proximities is near universal across manifold learning approaches and global structure is properly maintained using diffusion-based algorithms.

Geometry- and Accuracy-Preserving Random Forest Proximities

Random forests are considered one of the best out-of-the-box classification and regression algorithms due to their high level of predictive performance with relatively little tuning. Pairwise proximities can be computed from a trained random forest which measure the similarity between data points relative to the supervised task. Random forest proximities have been used in many applications including the identification of variable importance, data imputation, outlier detection, and data visualization. However, existing definitions of random forest proximities do not accurately reflect the data geometry learned by the random forest. In this paper, we introduce a novel definition of random forest proximities called Random Forest-Geometry- and Accuracy-Preserving proximities (RF-GAP). We prove that the proximity-weighted sum (regression) or majority vote (classification) using RF-GAP exactly match the out-of-bag random forest prediction, thus capturing the data geometry learned by the random forest. We empirically show that this improved geometric representation outperforms traditional random forest proximities in tasks such as data imputation and provides outlier detection and visualization results consistent with the learned data geometry.

Supervised Visualization for Data Exploration

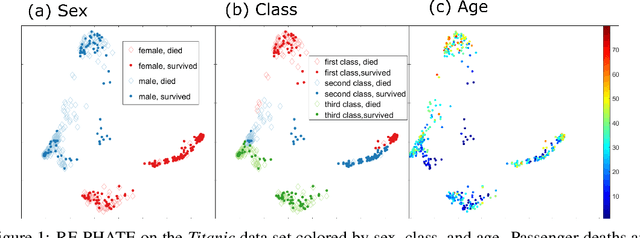
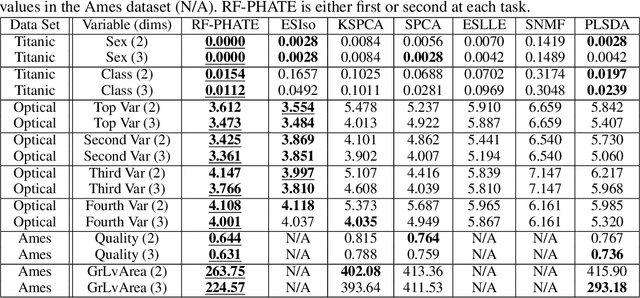
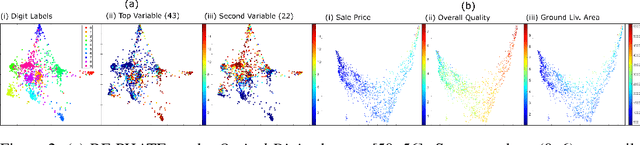
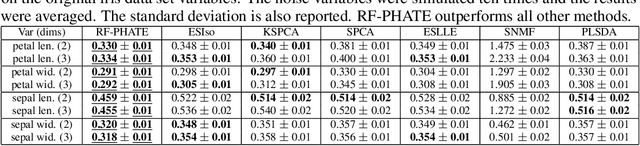
Dimensionality reduction is often used as an initial step in data exploration, either as preprocessing for classification or regression or for visualization. Most dimensionality reduction techniques to date are unsupervised; they do not take class labels into account (e.g., PCA, MDS, t-SNE, Isomap). Such methods require large amounts of data and are often sensitive to noise that may obfuscate important patterns in the data. Various attempts at supervised dimensionality reduction methods that take into account auxiliary annotations (e.g., class labels) have been successfully implemented with goals of increased classification accuracy or improved data visualization. Many of these supervised techniques incorporate labels in the loss function in the form of similarity or dissimilarity matrices, thereby creating over-emphasized separation between class clusters, which does not realistically represent the local and global relationships in the data. In addition, these approaches are often sensitive to parameter tuning, which may be difficult to configure without an explicit quantitative notion of visual superiority. In this paper, we describe a novel supervised visualization technique based on random forest proximities and diffusion-based dimensionality reduction. We show, both qualitatively and quantitatively, the advantages of our approach in retaining local and global structures in data, while emphasizing important variables in the low-dimensional embedding. Importantly, our approach is robust to noise and parameter tuning, thus making it simple to use while producing reliable visualizations for data exploration.