Model agnostic local variable importance for locally dependent relationships

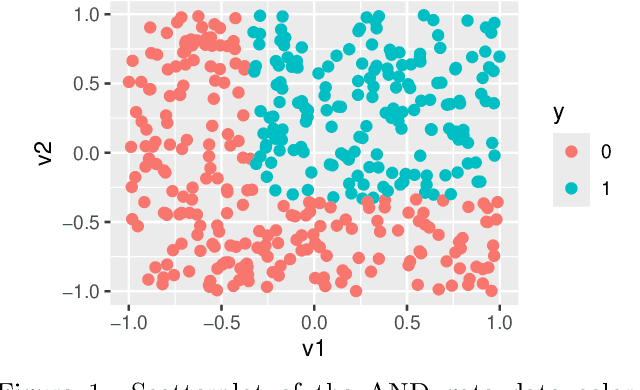
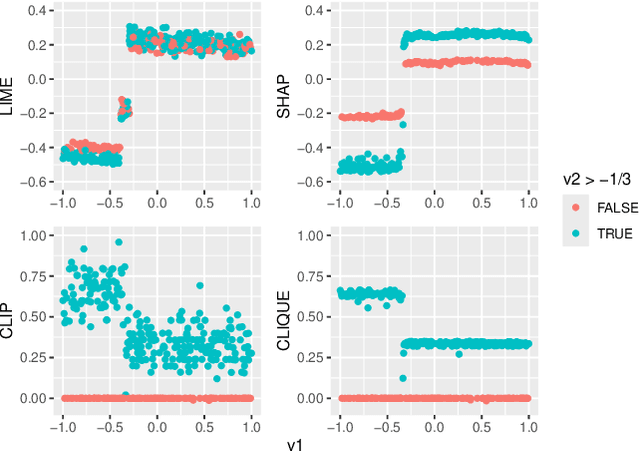
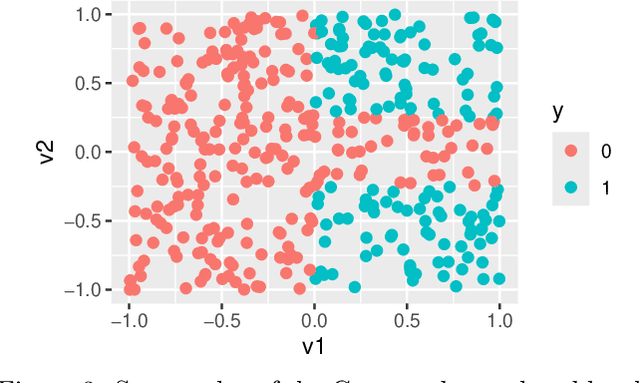
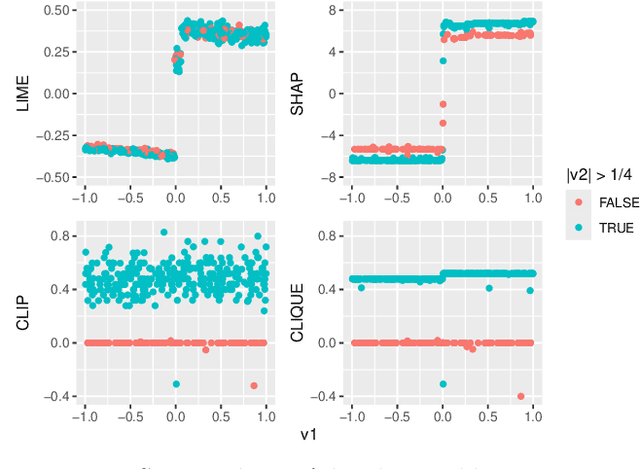
Global variable importance measures are commonly used to interpret machine learning model results. Local variable importance techniques assess how variables contribute to individual observations rather than the entire dataset. Current methods typically fail to accurately reflect locally dependent relationships between variables and instead focus on marginal importance values. Additionally, they are not natively adapted for multi-class classification problems. We propose a new model-agnostic method for calculating local variable importance, CLIQUE, that captures locally dependent relationships, contains improvements over permutation-based methods, and can be directly applied to multi-class classification problems. Simulated and real-world examples show that CLIQUE emphasizes locally dependent information and properly reduces bias in regions where variables do not affect the response.

Geometry- and Accuracy-Preserving Random Forest Proximities

Random forests are considered one of the best out-of-the-box classification and regression algorithms due to their high level of predictive performance with relatively little tuning. Pairwise proximities can be computed from a trained random forest which measure the similarity between data points relative to the supervised task. Random forest proximities have been used in many applications including the identification of variable importance, data imputation, outlier detection, and data visualization. However, existing definitions of random forest proximities do not accurately reflect the data geometry learned by the random forest. In this paper, we introduce a novel definition of random forest proximities called Random Forest-Geometry- and Accuracy-Preserving proximities (RF-GAP). We prove that the proximity-weighted sum (regression) or majority vote (classification) using RF-GAP exactly match the out-of-bag random forest prediction, thus capturing the data geometry learned by the random forest. We empirically show that this improved geometric representation outperforms traditional random forest proximities in tasks such as data imputation and provides outlier detection and visualization results consistent with the learned data geometry.

Supervised Visualization for Data Exploration

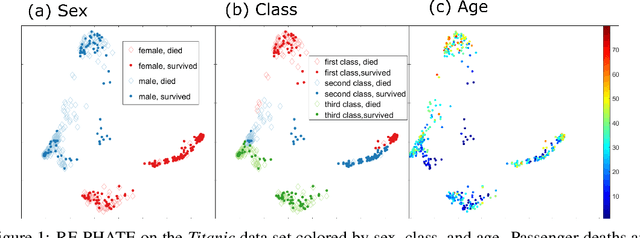
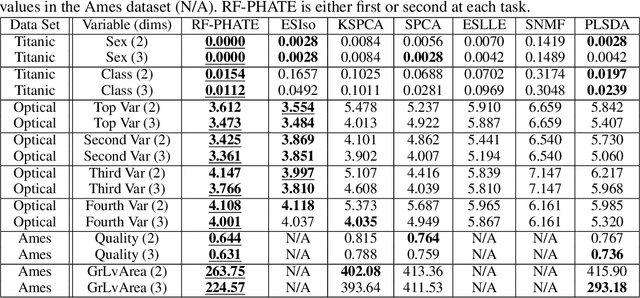
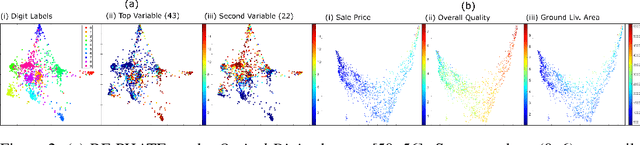
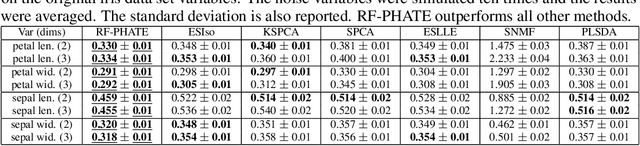
Dimensionality reduction is often used as an initial step in data exploration, either as preprocessing for classification or regression or for visualization. Most dimensionality reduction techniques to date are unsupervised; they do not take class labels into account (e.g., PCA, MDS, t-SNE, Isomap). Such methods require large amounts of data and are often sensitive to noise that may obfuscate important patterns in the data. Various attempts at supervised dimensionality reduction methods that take into account auxiliary annotations (e.g., class labels) have been successfully implemented with goals of increased classification accuracy or improved data visualization. Many of these supervised techniques incorporate labels in the loss function in the form of similarity or dissimilarity matrices, thereby creating over-emphasized separation between class clusters, which does not realistically represent the local and global relationships in the data. In addition, these approaches are often sensitive to parameter tuning, which may be difficult to configure without an explicit quantitative notion of visual superiority. In this paper, we describe a novel supervised visualization technique based on random forest proximities and diffusion-based dimensionality reduction. We show, both qualitatively and quantitatively, the advantages of our approach in retaining local and global structures in data, while emphasizing important variables in the low-dimensional embedding. Importantly, our approach is robust to noise and parameter tuning, thus making it simple to use while producing reliable visualizations for data exploration.