Forest-Guided Semantic Transport for Label-Supervised Manifold Alignment

Label-supervised manifold alignment bridges the gap between unsupervised and correspondence-based paradigms by leveraging shared label information to align multimodal datasets. Still, most existing methods rely on Euclidean geometry to model intra-domain relationships. This approach can fail when features are only weakly related to the task of interest, leading to noisy, semantically misleading structure and degraded alignment quality. To address this limitation, we introduce FoSTA (Forest-guided Semantic Transport Alignment), a scalable alignment framework that leverages forest-induced geometry to denoise intra-domain structure and recover task-relevant manifolds prior to alignment. FoSTA builds semantic representations directly from label-informed forest affinities and aligns them via fast, hierarchical semantic transport, capturing meaningful cross-domain relationships. Extensive comparisons with established baselines demonstrate that FoSTA improves correspondence recovery and label transfer on synthetic benchmarks and delivers strong performance in practical single-cell applications, including batch correction and biological conservation.

Scalable Tree Ensemble Proximities in Python

Tree ensemble methods such as Random Forests naturally induce supervised similarity measures through their decision tree structure, but existing implementations of proximities derived from tree ensembles typically suffer from quadratic time or memory complexity, limiting their scalability. In this work, we introduce a general framework for efficient proximity computation by defining a family of Separable Weighted Leaf-Collision Proximities. We show that any proximity measure in this family admits an exact sparse matrix factorization, restricting computation to leaf-level collisions and avoiding explicit pairwise comparisons. This formulation enables low-memory, scalable proximity computation using sparse linear algebra in Python. Empirical benchmarks demonstrate substantial runtime and memory improvements over traditional approaches, allowing tree ensemble proximities to scale efficiently to datasets with hundreds of thousands of samples on standard CPU hardware.

Lie Group Symmetry Discovery and Enforcement Using Vector Fields

Symmetry-informed machine learning can exhibit advantages over machine learning which fails to account for symmetry. Additionally, recent attention has been given to continuous symmetry discovery using vector fields which serve as infinitesimal generators for Lie group symmetries. In this paper, we extend the notion of non-affine symmetry discovery to functions defined by neural networks. We further extend work in this area by introducing symmetry enforcement of smooth models using vector fields. Finally, we extend work on symmetry discovery using vector fields by providing both theoretical and experimental material on the restriction of the symmetry search space to infinitesimal isometries.

Random Forest Autoencoders for Guided Representation Learning

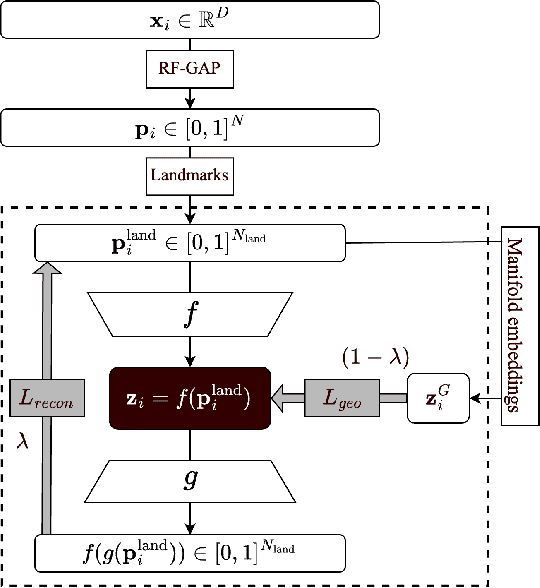
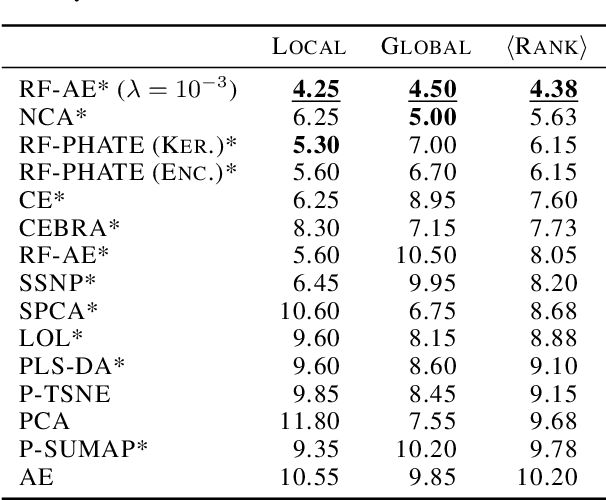
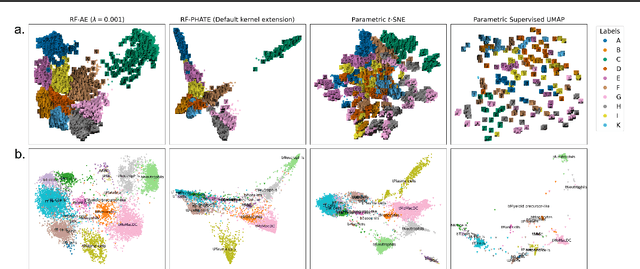
Decades of research have produced robust methods for unsupervised data visualization, yet supervised visualization$\unicode{x2013}$where expert labels guide representations$\unicode{x2013}$remains underexplored, as most supervised approaches prioritize classification over visualization. Recently, RF-PHATE, a diffusion-based manifold learning method leveraging random forests and information geometry, marked significant progress in supervised visualization. However, its lack of an explicit mapping function limits scalability and prevents application to unseen data, posing challenges for large datasets and label-scarce scenarios. To overcome these limitations, we introduce Random Forest Autoencoders (RF-AE), a neural network-based framework for out-of-sample kernel extension that combines the flexibility of autoencoders with the supervised learning strengths of random forests and the geometry captured by RF-PHATE. RF-AE enables efficient out-of-sample supervised visualization and outperforms existing methods, including RF-PHATE's standard kernel extension, in both accuracy and interpretability. Additionally, RF-AE is robust to the choice of hyper-parameters and generalizes to any kernel-based dimensionality reduction method.

Improved Background Estimation for Gas Plume Identification in Hyperspectral Images

Longwave infrared (LWIR) hyperspectral imaging can be used for many tasks in remote sensing, including detecting and identifying effluent gases by LWIR sensors on airborne platforms. Once a potential plume has been detected, it needs to be identified to determine exactly what gas or gases are present in the plume. During identification, the background underneath the plume needs to be estimated and removed to reveal the spectral characteristics of the gas of interest. Current standard practice is to use ``global" background estimation, where the average of all non-plume pixels is used to estimate the background for each pixel in the plume. However, if this global background estimate does not model the true background under the plume well, then the resulting signal can be difficult to identify correctly. The importance of proper background estimation increases when dealing with weak signals, large libraries of gases of interest, and with uncommon or heterogeneous backgrounds. In this paper, we propose two methods of background estimation, in addition to three existing methods, and compare each against global background estimation to determine which perform best at estimating the true background radiance under a plume, and for increasing identification confidence using a neural network classification model. We compare the different methods using 640 simulated plumes. We find that PCA is best at estimating the true background under a plume, with a median of 18,000 times less MSE compared to global background estimation. Our proposed K-Nearest Segments algorithm improves median neural network identification confidence by 53.2%.

Model agnostic local variable importance for locally dependent relationships

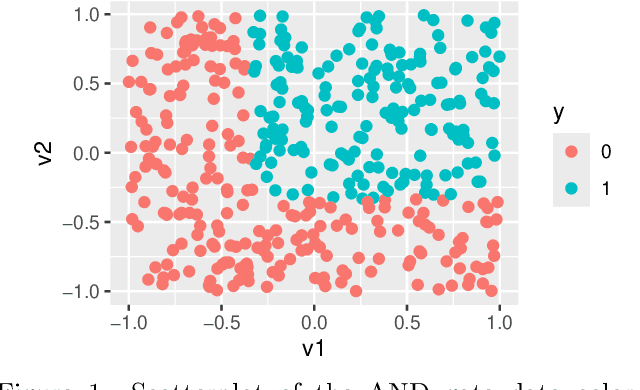
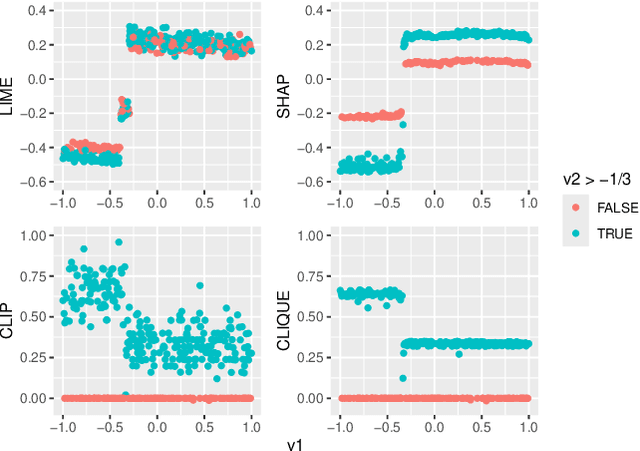
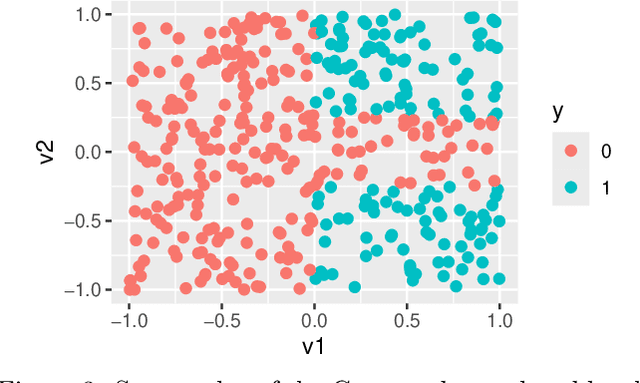
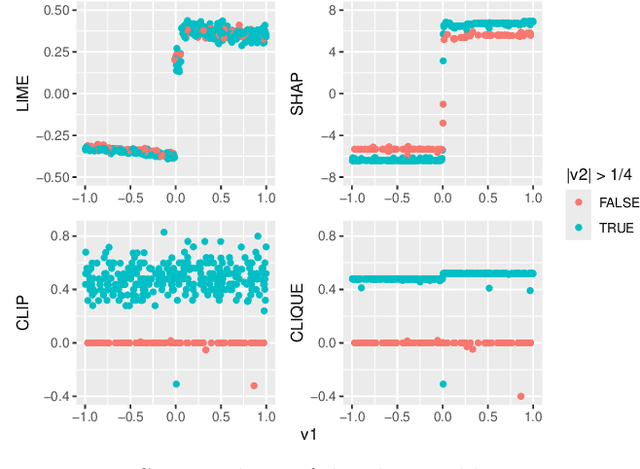
Global variable importance measures are commonly used to interpret machine learning model results. Local variable importance techniques assess how variables contribute to individual observations rather than the entire dataset. Current methods typically fail to accurately reflect locally dependent relationships between variables and instead focus on marginal importance values. Additionally, they are not natively adapted for multi-class classification problems. We propose a new model-agnostic method for calculating local variable importance, CLIQUE, that captures locally dependent relationships, contains improvements over permutation-based methods, and can be directly applied to multi-class classification problems. Simulated and real-world examples show that CLIQUE emphasizes locally dependent information and properly reduces bias in regions where variables do not affect the response.

Forest Proximities for Time Series

RF-GAP has recently been introduced as an improved random forest proximity measure. In this paper, we present PF-GAP, an extension of RF-GAP proximities to proximity forests, an accurate and efficient time series classification model. We use the forest proximities in connection with Multi-Dimensional Scaling to obtain vector embeddings of univariate time series, comparing the embeddings to those obtained using various time series distance measures. We also use the forest proximities alongside Local Outlier Factors to investigate the connection between misclassified points and outliers, comparing with nearest neighbor classifiers which use time series distance measures. We show that the forest proximities may exhibit a stronger connection between misclassified points and outliers than nearest neighbor classifiers.

Training-Free Guidance for Discrete Diffusion Models for Molecular Generation

Training-free guidance methods for continuous data have seen an explosion of interest due to the fact that they enable foundation diffusion models to be paired with interchangable guidance models. Currently, equivalent guidance methods for discrete diffusion models are unknown. We present a framework for applying training-free guidance to discrete data and demonstrate its utility on molecular graph generation tasks using the discrete diffusion model architecture of DiGress. We pair this model with guidance functions that return the proportion of heavy atoms that are a specific atom type and the molecular weight of the heavy atoms and demonstrate our method's ability to guide the data generation.

Enhancing Supervised Visualization through Autoencoder and Random Forest Proximities for Out-of-Sample Extension

The value of supervised dimensionality reduction lies in its ability to uncover meaningful connections between data features and labels. Common dimensionality reduction methods embed a set of fixed, latent points, but are not capable of generalizing to an unseen test set. In this paper, we provide an out-of-sample extension method for the random forest-based supervised dimensionality reduction method, RF-PHATE, combining information learned from the random forest model with the function-learning capabilities of autoencoders. Through quantitative assessment of various autoencoder architectures, we identify that networks that reconstruct random forest proximities are more robust for the embedding extension problem. Furthermore, by leveraging proximity-based prototypes, we achieve a 40% reduction in training time without compromising extension quality. Our method does not require label information for out-of-sample points, thus serving as a semi-supervised method, and can achieve consistent quality using only 10% of the training data.

Symmetry Discovery Beyond Affine Transformations

Symmetry detection has been shown to improve various machine learning tasks. In the context of continuous symmetry detection, current state of the art experiments are limited to the detection of affine transformations. Under the manifold assumption, we outline a framework for discovering continuous symmetry in data beyond the affine transformation group. We also provide a similar framework for discovering discrete symmetry. We experimentally compare our method to an existing method known as LieGAN and show that our method is competitive at detecting affine symmetries for large sample sizes and superior than LieGAN for small sample sizes. We also show our method is able to detect continuous symmetries beyond the affine group and is generally more computationally efficient than LieGAN.