Low Rank Multi-Dictionary Selection at Scale

The sparse dictionary coding framework represents signals as a linear combination of a few predefined dictionary atoms. It has been employed for images, time series, graph signals and recently for 2-way (or 2D) spatio-temporal data employing jointly temporal and spatial dictionaries. Large and over-complete dictionaries enable high-quality models, but also pose scalability challenges which are exacerbated in multi-dictionary settings. Hence, an important problem that we address in this paper is: How to scale multi-dictionary coding for large dictionaries and datasets? We propose a multi-dictionary atom selection technique for low-rank sparse coding named LRMDS. To enable scalability to large dictionaries and datasets, it progressively selects groups of row-column atom pairs based on their alignment with the data and performs convex relaxation coding via the corresponding sub-dictionaries. We demonstrate both theoretically and experimentally that when the data has a low-rank encoding with a sparse subset of the atoms, LRMDS is able to select them with strong guarantees under mild assumptions. Furthermore, we demonstrate the scalability and quality of LRMDS in both synthetic and real-world datasets and for a range of coding dictionaries. It achieves 3X to 10X speed-up compared to baselines, while obtaining up to two orders of magnitude improvement in representation quality on some of the real world datasets given a fixed target number of atoms.

Symmetry Discovery Beyond Affine Transformations

Symmetry detection has been shown to improve various machine learning tasks. In the context of continuous symmetry detection, current state of the art experiments are limited to the detection of affine transformations. Under the manifold assumption, we outline a framework for discovering continuous symmetry in data beyond the affine transformation group. We also provide a similar framework for discovering discrete symmetry. We experimentally compare our method to an existing method known as LieGAN and show that our method is competitive at detecting affine symmetries for large sample sizes and superior than LieGAN for small sample sizes. We also show our method is able to detect continuous symmetries beyond the affine group and is generally more computationally efficient than LieGAN.

Fat Shattering, Joint Measurability, and PAC Learnability of POVM Hypothesis Classes

We characterize learnability for quantum measurement classes by establishing matching necessary and sufficient conditions for their PAC learnability, along with corresponding sample complexity bounds, in the setting where the learner is given access only to prepared quantum states. We first probe the results from previous works on this setting. We show that the empirical risk defined in previous works and matching the definition in the classical theory fails to satisfy the uniform convergence property enjoyed in the classical setting for some learnable classes. Moreover, we show that VC dimension generalization upper bounds in previous work are frequently infinite, even for finite-dimensional POVM classes. To surmount the failure of the standard ERM to satisfy uniform convergence, we define a new learning rule -- denoised ERM. We show this to be a universal learning rule for POVM and probabilistically observed concept classes, and the condition for it to satisfy uniform convergence is finite fat shattering dimension of the class. We give quantitative sample complexity upper and lower bounds for learnability in terms of finite fat-shattering dimension and a notion of approximate finite partitionability into approximately jointly measurable subsets, which allow for sample reuse. We then show that finite fat shattering dimension implies finite coverability by approximately jointly measurable subsets, leading to our matching conditions. We also show that every measurement class defined on a finite-dimensional Hilbert space is PAC learnable. We illustrate our results on several example POVM classes.

Promise and Limitations of Supervised Optimal Transport-Based Graph Summarization via Information Theoretic Measures

Graph summarization is the problem of producing smaller graph representations of an input graph dataset, in such a way that the smaller compressed graphs capture relevant structural information for downstream tasks. There is a recent graph summarization method that formulates an optimal transport-based framework that allows prior information about node, edge, and attribute importance (never defined in that work) to be incorporated into the graph summarization process. However, very little is known about the statistical properties of this framework. To elucidate this question, we consider the problem of supervised graph summarization, wherein by using information theoretic measures we seek to preserve relevant information about a class label. To gain a theoretical perspective on the supervised summarization problem itself, we first formulate it in terms of maximizing the Shannon mutual information between the summarized graph and the class label. We show an NP-hardness of approximation result for this problem, thereby constraining what one should expect from proposed solutions. We then propose a summarization method that incorporates mutual information estimates between random variables associated with sample graphs and class labels into the optimal transport compression framework. We empirically show performance improvements over previous works in terms of classification accuracy and time on synthetic and certain real datasets. We also theoretically explore the limitations of the optimal transport approach for the supervised summarization problem and we show that it fails to satisfy a certain desirable information monotonicity property.

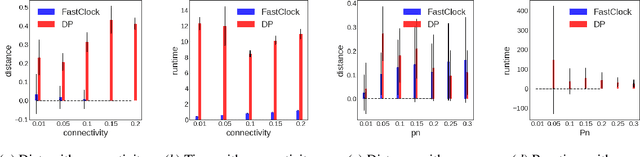
Temporal Scale Estimation for Oversampled Network Cascades: Theory, Algorithms, and Experiment

Spreading processes on graphs arise in a host of application domains, from the study of online social networks to viral marketing to epidemiology. Various discrete-time probabilistic models for spreading processes have been proposed. These are used for downstream statistical estimation and prediction problems, often involving messages or other information that is transmitted along with infections caused by the process. It is thus important to design models of cascade observation that take into account phenomena that lead to uncertainty about the process state at any given time. We highlight one such phenomenon -- temporal distortion -- caused by a misalignment between the rate at which observations of a cascade process are made and the rate at which the process itself operates, and argue that failure to correct for it results in degradation of performance on downstream statistical tasks. To address these issues, we formulate the clock estimation problem in terms of a natural distortion measure. We give a clock estimation algorithm, which we call FastClock, that runs in linear time in the size of its input and is provably statistically accurate for a broad range of model parameters when cascades are generated from the independent cascade process with known parameters and when the underlying graph is Erd\H{o}s-R\'enyi. We further give empirical results on the performance of our algorithm in comparison to the state of the art estimator, a likelihood proxy maximization-based estimator implemented via dynamic programming. We find that, in a broad parameter regime, our algorithm substantially outperforms the dynamic programming algorithm in terms of both running time and accuracy.

The Power of Graph Convolutional Networks to Distinguish Random Graph Models: Short Version

Graph convolutional networks (GCNs) are a widely used method for graph representation learning. We investigate the power of GCNs, as a function of their number of layers, to distinguish between different random graph models on the basis of the embeddings of their sample graphs. In particular, the graph models that we consider arise from graphons, which are the most general possible parameterizations of infinite exchangeable graph models and which are the central objects of study in the theory of dense graph limits. We exhibit an infinite class of graphons that are well-separated in terms of cut distance and are indistinguishable by a GCN with nonlinear activation functions coming from a certain broad class if its depth is at least logarithmic in the size of the sample graph. These results theoretically match empirical observations of several prior works. Finally, we show a converse result that for pairs of graphons satisfying a degree profile separation property, a very simple GCN architecture suffices for distinguishability. To prove our results, we exploit a connection to random walks on graphs.

The Power of Graph Convolutional Networks to Distinguish Random Graph Models

Graph convolutional networks (GCNs) are a widely used method for graph representation learning. We investigate the power of GCNs, as a function of their number of layers, to distinguish between different random graph models on the basis of the embeddings of their sample graphs. In particular, the graph models that we consider arise from graphons, which are the most general possible parameterizations of infinite exchangeable graph models and which are the central objects of study in the theory of dense graph limits. We exhibit an infinite class of graphons that are well-separated in terms of cut distance and are indistinguishable by a GCN with nonlinear activation functions coming from a certain broad class if its depth is at least logarithmic in the size of the sample graph, and furthermore show that, for this application, ReLU activation functions and non-identity weight matrices with non-negative entries do not help in terms of distinguishing power. These results theoretically match empirical observations of several prior works. Finally, we show that for pairs of graphons satisfying a degree profile separation property, a very simple GCN architecture suffices for distinguishability. To prove our results, we exploit a connection to random walks on graphs.

Goodness of Fit Testing for Dynamic Networks

Numerous networks in the real world change over time, in the sense that nodes and edges enter and leave the networks. Various dynamic random graph models have been proposed to explain the macroscopic properties of these systems and to provide a foundation for statistical inferences and predictions. It is of interest to have a rigorous way to determine how well these models match observed networks. We thus ask the following goodness of fit question: given a sequence of observations/snapshots of a growing random graph, along with a candidate model $M$, can we determine whether the snapshots came from $M$ or from some arbitrary alternative model that is well-separated from $M$ in some natural metric? We formulate this problem precisely and boil it down to goodness of fit testing for graph-valued, infinite-state Markov processes and exhibit and analyze a test based on a procedure that we call non-stationary sampling for a natural class of models.