Efficiency Boost in Decentralized Optimization: Reimagining Neighborhood Aggregation with Minimal Overhead

In today's data-sensitive landscape, distributed learning emerges as a vital tool, not only fortifying privacy measures but also streamlining computational operations. This becomes especially crucial within fully decentralized infrastructures where local processing is imperative due to the absence of centralized aggregation. Here, we introduce DYNAWEIGHT, a novel framework to information aggregation in multi-agent networks. DYNAWEIGHT offers substantial acceleration in decentralized learning with minimal additional communication and memory overhead. Unlike traditional static weight assignments, such as Metropolis weights, DYNAWEIGHT dynamically allocates weights to neighboring servers based on their relative losses on local datasets. Consequently, it favors servers possessing diverse information, particularly in scenarios of substantial data heterogeneity. Our experiments on various datasets MNIST, CIFAR10, and CIFAR100 incorporating various server counts and graph topologies, demonstrate notable enhancements in training speeds. Notably, DYNAWEIGHT functions as an aggregation scheme compatible with any underlying server-level optimization algorithm, underscoring its versatility and potential for widespread integration.

DeepMech: A Machine Learning Framework for Chemical Reaction Mechanism Prediction

Prediction of complete step-by-step chemical reaction mechanisms (CRMs) remains a major challenge. Whereas the traditional approaches in CRM tasks rely on expert-driven experiments or costly quantum chemical computations, contemporary deep learning (DL) alternatives ignore key intermediates and mechanistic steps and often suffer from hallucinations. We present DeepMech, an interpretable graph-based DL framework employing atom- and bond-level attention, guided by generalized templates of mechanistic operations (TMOps), to generate CRMs. Trained on our curated ReactMech dataset (~30K CRMs with 100K atom-mapped and mass-balanced elementary steps), DeepMech achieves 98.98+/-0.12% accuracy in predicting elementary steps and 95.94+/-0.21% in complete CRM tasks, besides maintaining high fidelity even in out-of-distribution scenarios as well as in predicting side and/or byproducts. Extension to multistep CRMs relevant to prebiotic chemistry, demonstrates the ability of DeepMech in effectively reconstructing pathways from simple primordial substrates to complex biomolecules such as serine and aldopentose. Attention analysis identifies reactive atoms/bonds in line with chemical intuition, rendering our model interpretable and suitable for reaction design.

Together We Rise: Optimizing Real-Time Multi-Robot Task Allocation using Coordinated Heterogeneous Plays

Efficient task allocation among multiple robots is crucial for optimizing productivity in modern warehouses, particularly in response to the increasing demands of online order fulfillment. This paper addresses the real-time multi-robot task allocation (MRTA) problem in dynamic warehouse environments, where tasks emerge with specified start and end locations. The objective is to minimize both the total travel distance of robots and delays in task completion, while also considering practical constraints such as battery management and collision avoidance. We introduce MRTAgent, a dual-agent Reinforcement Learning (RL) framework inspired by self-play, designed to optimize task assignments and robot selection to ensure timely task execution. For safe navigation, a modified linear quadratic controller (LQR) approach is employed. To the best of our knowledge, MRTAgent is the first framework to address all critical aspects of practical MRTA problems while supporting continuous robot movements.

$TAR^2$: Temporal-Agent Reward Redistribution for Optimal Policy Preservation in Multi-Agent Reinforcement Learning

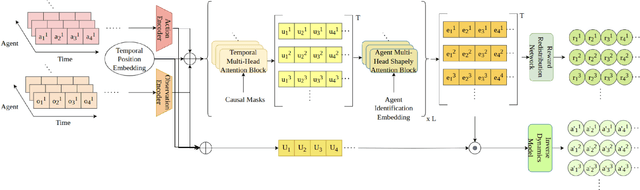
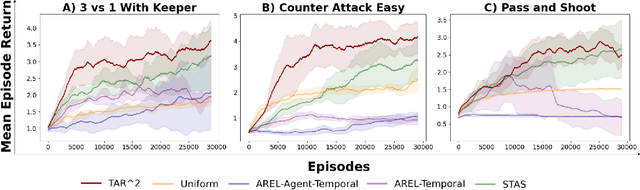
In cooperative multi-agent reinforcement learning (MARL), learning effective policies is challenging when global rewards are sparse and delayed. This difficulty arises from the need to assign credit across both agents and time steps, a problem that existing methods often fail to address in episodic, long-horizon tasks. We propose Temporal-Agent Reward Redistribution $TAR^2$, a novel approach that decomposes sparse global rewards into agent-specific, time-step-specific components, thereby providing more frequent and accurate feedback for policy learning. Theoretically, we show that $TAR^2$ (i) aligns with potential-based reward shaping, preserving the same optimal policies as the original environment, and (ii) maintains policy gradient update directions identical to those under the original sparse reward, ensuring unbiased credit signals. Empirical results on two challenging benchmarks, SMACLite and Google Research Football, demonstrate that $TAR^2$ significantly stabilizes and accelerates convergence, outperforming strong baselines like AREL and STAS in both learning speed and final performance. These findings establish $TAR^2$ as a principled and practical solution for agent-temporal credit assignment in sparse-reward multi-agent systems.

Agent-Temporal Credit Assignment for Optimal Policy Preservation in Sparse Multi-Agent Reinforcement Learning

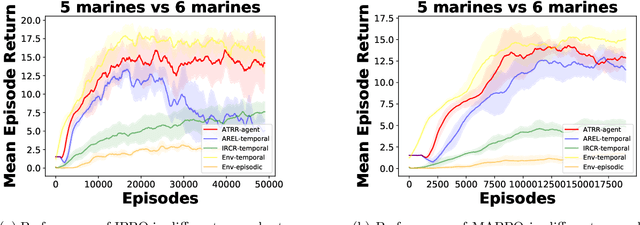
In multi-agent environments, agents often struggle to learn optimal policies due to sparse or delayed global rewards, particularly in long-horizon tasks where it is challenging to evaluate actions at intermediate time steps. We introduce Temporal-Agent Reward Redistribution (TAR$^2$), a novel approach designed to address the agent-temporal credit assignment problem by redistributing sparse rewards both temporally and across agents. TAR$^2$ decomposes sparse global rewards into time-step-specific rewards and calculates agent-specific contributions to these rewards. We theoretically prove that TAR$^2$ is equivalent to potential-based reward shaping, ensuring that the optimal policy remains unchanged. Empirical results demonstrate that TAR$^2$ stabilizes and accelerates the learning process. Additionally, we show that when TAR$^2$ is integrated with single-agent reinforcement learning algorithms, it performs as well as or better than traditional multi-agent reinforcement learning methods.

Distributed Optimization via Energy Conservation Laws in Dilated Coordinates

Optimizing problems in a distributed manner is critical for systems involving multiple agents with private data. Despite substantial interest, a unified method for analyzing the convergence rates of distributed optimization algorithms is lacking. This paper introduces an energy conservation approach for analyzing continuous-time dynamical systems in dilated coordinates. Instead of directly analyzing dynamics in the original coordinate system, we establish a conserved quantity, akin to physical energy, in the dilated coordinate system. Consequently, convergence rates can be explicitly expressed in terms of the inverse time-dilation factor. Leveraging this generalized approach, we formulate a novel second-order distributed accelerated gradient flow with a convergence rate of $O\left(1/t^{2-\epsilon}\right)$ in time $t$ for $\epsilon>0$. We then employ a semi second-order symplectic Euler discretization to derive a rate-matching algorithm with a convergence rate of $O\left(1/k^{2-\epsilon}\right)$ in $k$ iterations. To the best of our knowledge, this represents the most favorable convergence rate for any distributed optimization algorithm designed for smooth convex optimization. Its accelerated convergence behavior is benchmarked against various state-of-the-art distributed optimization algorithms on practical, large-scale problems.

A Methodology Establishing Linear Convergence of Adaptive Gradient Methods under PL Inequality

Adaptive gradient-descent optimizers are the standard choice for training neural network models. Despite their faster convergence than gradient-descent and remarkable performance in practice, the adaptive optimizers are not as well understood as vanilla gradient-descent. A reason is that the dynamic update of the learning rate that helps in faster convergence of these methods also makes their analysis intricate. Particularly, the simple gradient-descent method converges at a linear rate for a class of optimization problems, whereas the practically faster adaptive gradient methods lack such a theoretical guarantee. The Polyak-{\L}ojasiewicz (PL) inequality is the weakest known class, for which linear convergence of gradient-descent and its momentum variants has been proved. Therefore, in this paper, we prove that AdaGrad and Adam, two well-known adaptive gradient methods, converge linearly when the cost function is smooth and satisfies the PL inequality. Our theoretical framework follows a simple and unified approach, applicable to both batch and stochastic gradients, which can potentially be utilized in analyzing linear convergence of other variants of Adam.

ReactAIvate: A Deep Learning Approach to Predicting Reaction Mechanisms and Unmasking Reactivity Hotspots

A chemical reaction mechanism (CRM) is a sequence of molecular-level events involving bond-breaking/forming processes, generating transient intermediates along the reaction pathway as reactants transform into products. Understanding such mechanisms is crucial for designing and discovering new reactions. One of the currently available methods to probe CRMs is quantum mechanical (QM) computations. The resource-intensive nature of QM methods and the scarcity of mechanism-based datasets motivated us to develop reliable ML models for predicting mechanisms. In this study, we created a comprehensive dataset with seven distinct classes, each representing uniquely characterized elementary steps. Subsequently, we developed an interpretable attention-based GNN that achieved near-unity and 96% accuracy, respectively for reaction step classification and the prediction of reactive atoms in each such step, capturing interactions between the broader reaction context and local active regions. The near-perfect classification enables accurate prediction of both individual events and the entire CRM, mitigating potential drawbacks of Seq2Seq approaches, where a wrongly predicted character leads to incoherent CRM identification. In addition to interpretability, our model adeptly identifies key atom(s) even from out-of-distribution classes. This generalizabilty allows for the inclusion of new reaction types in a modular fashion, thus will be of value to experts for understanding the reactivity of new molecules.

Linear Convergence of Pre-Conditioned PI Consensus Algorithm under Restricted Strong Convexity

This paper considers solving distributed convex optimization problems in peer-to-peer multi-agent networks. The network is assumed to be synchronous and connected. By using the proportional-integral (PI) control strategy, various algorithms with fixed stepsize have been developed. The earliest among them is the PI consensus algorithm. Using Lyapunov theory, we guarantee exponential convergence of the PI consensus algorithm for restricted strongly convex functions with rate-matching discretization, without requiring convexity of individual local cost functions, for the first time. In order to accelerate the PI consensus algorithm, we incorporate local pre-conditioning in the form of constant positive definite matrices and numerically validate its efficiency compared to the prominent distributed convex optimization algorithms. Unlike classical pre-conditioning, where only the gradients are multiplied by a pre-conditioner, the proposed pre-conditioning modifies both the gradients and the consensus terms, thereby controlling the effect of the communication graph between the agents on the PI consensus algorithm.

Generalized Gradient Flows with Provable Fixed-Time Convergence and Fast Evasion of Non-Degenerate Saddle Points

Gradient-based first-order convex optimization algorithms find widespread applicability in a variety of domains, including machine learning tasks. Motivated by the recent advances in fixed-time stability theory of continuous-time dynamical systems, we introduce a generalized framework for designing accelerated optimization algorithms with strongest convergence guarantees that further extend to a subclass of non-convex functions. In particular, we introduce the \emph{GenFlow} algorithm and its momentum variant that provably converge to the optimal solution of objective functions satisfying the Polyak-{\L}ojasiewicz (PL) inequality, in a fixed-time. Moreover for functions that admit non-degenerate saddle-points, we show that for the proposed GenFlow algorithm, the time required to evade these saddle-points is bounded uniformly for all initial conditions. Finally, for strongly convex-strongly concave minimax problems whose optimal solution is a saddle point, a similar scheme is shown to arrive at the optimal solution again in a fixed-time. The superior convergence properties of our algorithm are validated experimentally on a variety of benchmark datasets.