Failure Prediction from Limited Hardware Demonstrations

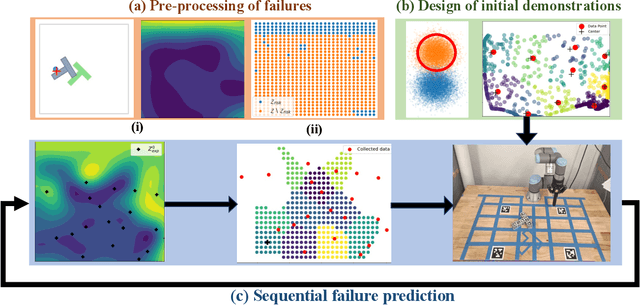
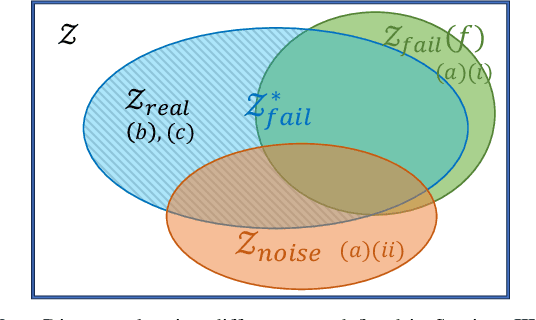
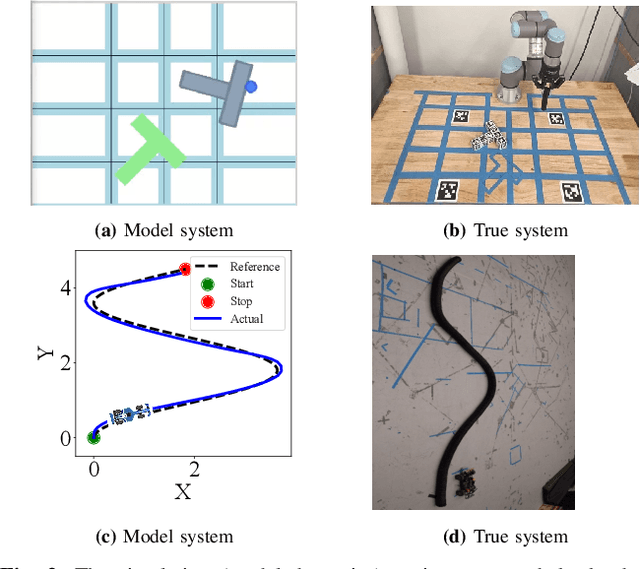
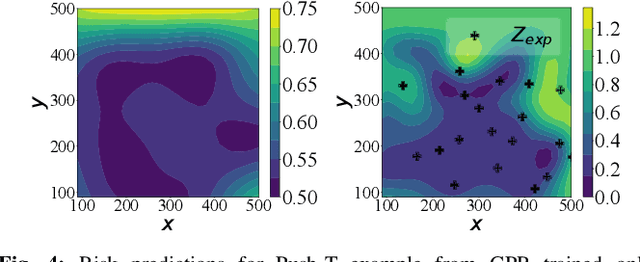
Prediction of failures in real-world robotic systems either requires accurate model information or extensive testing. Partial knowledge of the system model makes simulation-based failure prediction unreliable. Moreover, obtaining such demonstrations is expensive, and could potentially be risky for the robotic system to repeatedly fail during data collection. This work presents a novel three-step methodology for discovering failures that occur in the true system by using a combination of a limited number of demonstrations from the true system and the failure information processed through sampling-based testing of a model dynamical system. Given a limited budget $N$ of demonstrations from true system and a model dynamics (with potentially large modeling errors), the proposed methodology comprises of a) exhaustive simulations for discovering algorithmic failures using the model dynamics; b) design of initial $N_1$ demonstrations of the true system using Bayesian inference to learn a Gaussian process regression (GPR)-based failure predictor; and c) iterative $N - N_1$ demonstrations of the true system for updating the failure predictor. To illustrate the efficacy of the proposed methodology, we consider: a) the failure discovery for the task of pushing a T block to a fixed target region with UR3E collaborative robot arm using a diffusion policy; and b) the failure discovery for an F1-Tenth racing car tracking a given raceline under an LQR control policy.

Large Language Models to the Rescue: Deadlock Resolution in Multi-Robot Systems

Multi-agent robotic systems are prone to deadlocks in an obstacle environment where the system can get stuck away from its desired location under a smooth low-level control policy. Without an external intervention, often in terms of a high-level command, it is not possible to guarantee that just a low-level control policy can resolve such deadlocks. Utilizing the generalizability and low data requirements of large language models (LLMs), this paper explores the possibility of using LLMs for deadlock resolution. We propose a hierarchical control framework where an LLM resolves deadlocks by assigning a leader and direction for the leader to move along. A graph neural network (GNN) based low-level distributed control policy executes the assigned plan. We systematically study various prompting techniques to improve LLM's performance in resolving deadlocks. In particular, as part of prompt engineering, we provide in-context examples for LLMs. We conducted extensive experiments on various multi-robot environments with up to 15 agents and 40 obstacles. Our results demonstrate that LLM-based high-level planners are effective in resolving deadlocks in MRS.

GCBF+: A Neural Graph Control Barrier Function Framework for Distributed Safe Multi-Agent Control

Distributed, scalable, and safe control of large-scale multi-agent systems (MAS) is a challenging problem. In this paper, we design a distributed framework for safe multi-agent control in large-scale environments with obstacles, where a large number of agents are required to maintain safety using only local information and reach their goal locations. We introduce a new class of certificates, termed graph control barrier function (GCBF), which are based on the well-established control barrier function (CBF) theory for safety guarantees and utilize a graph structure for scalable and generalizable distributed control of MAS. We develop a novel theoretical framework to prove the safety of an arbitrary-sized MAS with a single GCBF. We propose a new training framework GCBF+ that uses graph neural networks (GNNs) to parameterize a candidate GCBF and a distributed control policy. The proposed framework is distributed and is capable of directly taking point clouds from LiDAR, instead of actual state information, for real-world robotic applications. We illustrate the efficacy of the proposed method through various hardware experiments on a swarm of drones with objectives ranging from exchanging positions to docking on a moving target without collision. Additionally, we perform extensive numerical experiments, where the number and density of agents, as well as the number of obstacles, increase. Empirical results show that in complex environments with nonlinear agents (e.g., Crazyflie drones) GCBF+ outperforms the handcrafted CBF-based method with the best performance by up to 20% for relatively small-scale MAS for up to 256 agents, and leading reinforcement learning (RL) methods by up to 40% for MAS with 1024 agents. Furthermore, the proposed method does not compromise on the performance, in terms of goal reaching, for achieving high safety rates, which is a common trade-off in RL-based methods.

Learning Safe Control for Multi-Robot Systems: Methods, Verification, and Open Challenges

In this survey, we review the recent advances in control design methods for robotic multi-agent systems (MAS), focussing on learning-based methods with safety considerations. We start by reviewing various notions of safety and liveness properties, and modeling frameworks used for problem formulation of MAS. Then we provide a comprehensive review of learning-based methods for safe control design for multi-robot systems. We start with various types of shielding-based methods, such as safety certificates, predictive filters, and reachability tools. Then, we review the current state of control barrier certificate learning in both a centralized and distributed manner, followed by a comprehensive review of multi-agent reinforcement learning with a particular focus on safety. Next, we discuss the state-of-the-art verification tools for the correctness of learning-based methods. Based on the capabilities and the limitations of the state of the art methods in learning and verification for MAS, we identify various broad themes for open challenges: how to design methods that can achieve good performance along with safety guarantees; how to decompose single-agent based centralized methods for MAS; how to account for communication-related practical issues; and how to assess transfer of theoretical guarantees to practice.

Neural Network-based Fault Detection and Identification for Quadrotors using Dynamic Symmetry

Autonomous robotic systems, such as quadrotors, are susceptible to actuator faults, and for the safe operation of such systems, timely detection and isolation of these faults is essential. Neural networks can be used for verification of actuator performance via online actuator fault detection with high accuracy. In this paper, we develop a novel model-free fault detection and isolation (FDI) framework for quadrotor systems using long-short-term memory (LSTM) neural network architecture. The proposed framework only uses system output data and the commanded control input and requires no knowledge of the system model. Utilizing the symmetry in quadrotor dynamics, we train the FDI for fault in just one of the motors (e.g., motor $\# 2$), and the trained FDI can predict faults in any of the motors. This reduction in search space enables us to design an FDI for partial fault as well as complete fault scenarios. Numerical experiments illustrate that the proposed NN-FDI correctly verifies the actuator performance and identifies partial as well as complete faults with over $90\%$ prediction accuracy. We also illustrate that model-free NN-FDI performs at par with model-based FDI, and is robust to model uncertainties as well as distribution shifts in input data.

Fixed-Time Convergence for a Class of Nonconvex-Nonconcave Min-Max Problems

This study develops a fixed-time convergent saddle point dynamical system for solving min-max problems under a relaxation of standard convexity-concavity assumption. In particular, it is shown that by leveraging the dynamical systems viewpoint of an optimization algorithm, accelerated convergence to a saddle point can be obtained. Instead of requiring the objective function to be strongly-convex--strongly-concave (as necessitated for accelerated convergence of several saddle-point algorithms), uniform fixed-time convergence is guaranteed for functions satisfying only the two-sided Polyak-{\L}ojasiewicz (PL) inequality. A large number of practical problems, including the robust least squares estimation, are known to satisfy the two-sided PL inequality. The proposed method achieves arbitrarily fast convergence compared to any other state-of-the-art method with linear or even super-linear convergence, as also corroborated in numerical case studies.

Breaking the Convergence Barrier: Optimization via Fixed-Time Convergent Flows

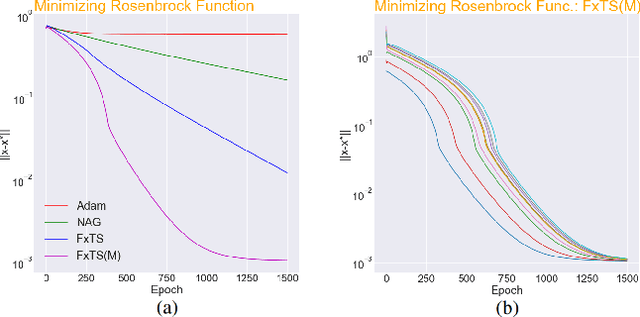
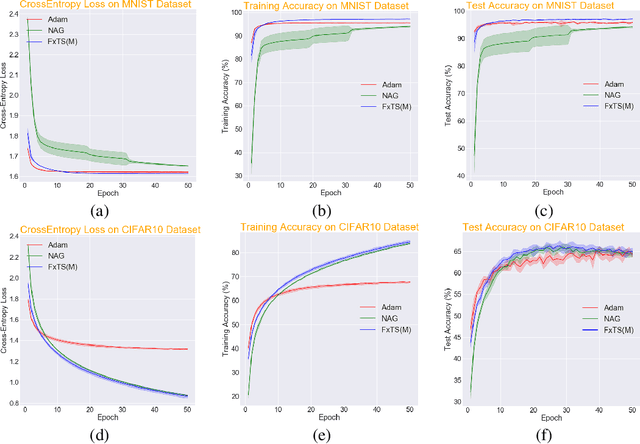
Accelerated gradient methods are the cornerstones of large-scale, data-driven optimization problems that arise naturally in machine learning and other fields concerning data analysis. We introduce a gradient-based optimization framework for achieving acceleration, based on the recently introduced notion of fixed-time stability of dynamical systems. The method presents itself as a generalization of simple gradient-based methods suitably scaled to achieve convergence to the optimizer in a fixed-time, independent of the initialization. We achieve this by first leveraging a continuous-time framework for designing fixed-time stable dynamical systems, and later providing a consistent discretization strategy, such that the equivalent discrete-time algorithm tracks the optimizer in a practically fixed number of iterations. We also provide a theoretical analysis of the convergence behavior of the proposed gradient flows, and their robustness to additive disturbances for a range of functions obeying strong convexity, strict convexity, and possibly nonconvexity but satisfying the Polyak-{\L}ojasiewicz inequality. We also show that the regret bound on the convergence rate is constant by virtue of the fixed-time convergence. The hyperparameters have intuitive interpretations and can be tuned to fit the requirements on the desired convergence rates. We validate the accelerated convergence properties of the proposed schemes on a range of numerical examples against the state-of-the-art optimization algorithms. Our work provides insights on developing novel optimization algorithms via discretization of continuous-time flows.