Failure Prediction from Limited Hardware Demonstrations

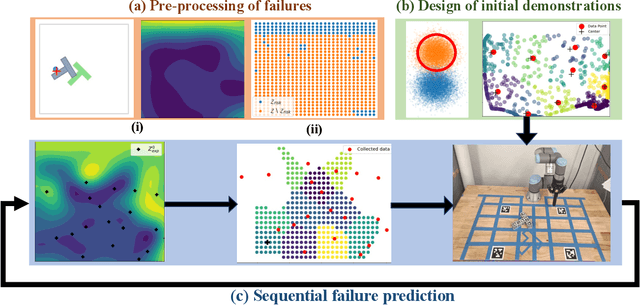
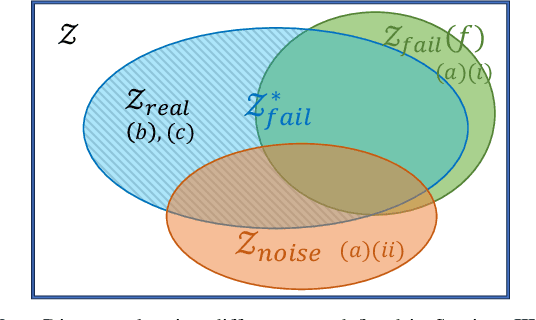
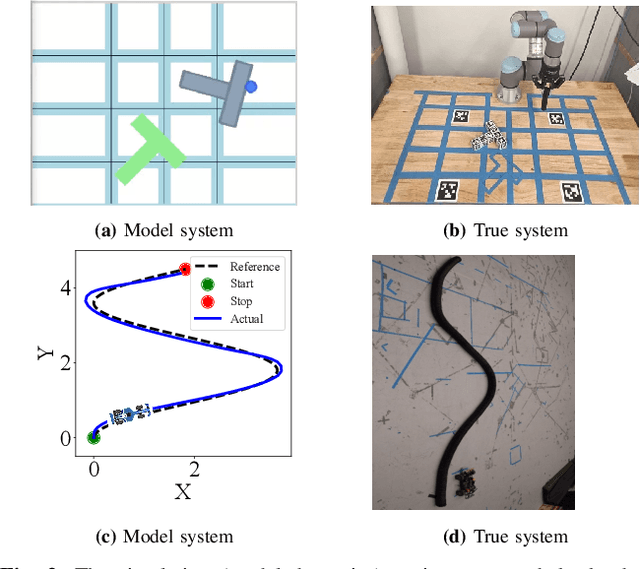
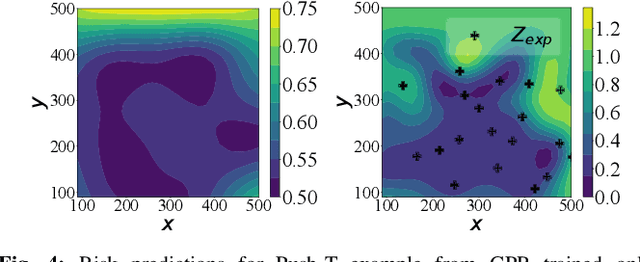
Prediction of failures in real-world robotic systems either requires accurate model information or extensive testing. Partial knowledge of the system model makes simulation-based failure prediction unreliable. Moreover, obtaining such demonstrations is expensive, and could potentially be risky for the robotic system to repeatedly fail during data collection. This work presents a novel three-step methodology for discovering failures that occur in the true system by using a combination of a limited number of demonstrations from the true system and the failure information processed through sampling-based testing of a model dynamical system. Given a limited budget $N$ of demonstrations from true system and a model dynamics (with potentially large modeling errors), the proposed methodology comprises of a) exhaustive simulations for discovering algorithmic failures using the model dynamics; b) design of initial $N_1$ demonstrations of the true system using Bayesian inference to learn a Gaussian process regression (GPR)-based failure predictor; and c) iterative $N - N_1$ demonstrations of the true system for updating the failure predictor. To illustrate the efficacy of the proposed methodology, we consider: a) the failure discovery for the task of pushing a T block to a fixed target region with UR3E collaborative robot arm using a diffusion policy; and b) the failure discovery for an F1-Tenth racing car tracking a given raceline under an LQR control policy.

Fast and Modular Autonomy Software for Autonomous Racing Vehicles

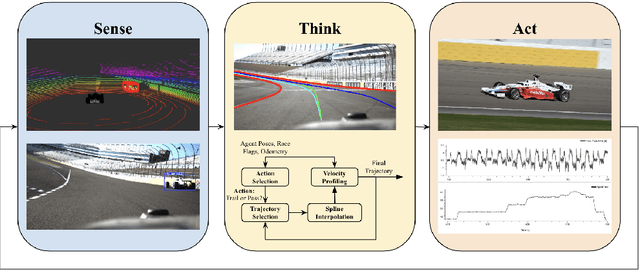
Autonomous motorsports aim to replicate the human racecar driver with software and sensors. As in traditional motorsports, Autonomous Racing Vehicles (ARVs) are pushed to their handling limits in multi-agent scenarios at extremely high ($\geq 150mph$) speeds. This Operational Design Domain (ODD) presents unique challenges across the autonomy stack. The Indy Autonomous Challenge (IAC) is an international competition aiming to advance autonomous vehicle development through ARV competitions. While far from challenging what a human racecar driver can do, the IAC is pushing the state of the art by facilitating full-sized ARV competitions. This paper details the MIT-Pitt-RW Team's approach to autonomous racing in the IAC. In this work, we present our modular and fast approach to agent detection, motion planning and controls to create an autonomy stack. We also provide analysis of the performance of the software stack in single and multi-agent scenarios for rapid deployment in a fast-paced competition environment. We also cover what did and did not work when deployed on a physical system the Dallara AV-21 platform and potential improvements to address these shortcomings. Finally, we convey lessons learned and discuss limitations and future directions for improvement.

On the stability of second order gradient descent for time varying convex functions

Gradient based optimization algorithms deployed in Machine Learning (ML) applications are often analyzed and compared by their convergence rates or regret bounds. While these rates and bounds convey valuable information they don't always directly translate to stability guarantees. Stability and similar concepts, like robustness, will become ever more important as we move towards deploying models in real-time and safety critical systems. In this work we build upon the results in Gaudio et al. 2021 and Moreu and Annaswamy 2022 for second order gradient descent when applied to explicitly time varying cost functions and provide more general stability guarantees. These more general results can aid in the design and certification of these optimization schemes so as to help ensure safe and reliable deployment for real-time learning applications. We also hope that the techniques provided here will stimulate and cross-fertilize the analysis that occurs on the same algorithms from the online learning and stochastic optimization communities.

RADIUM: Predicting and Repairing End-to-End Robot Failures using Gradient-Accelerated Sampling

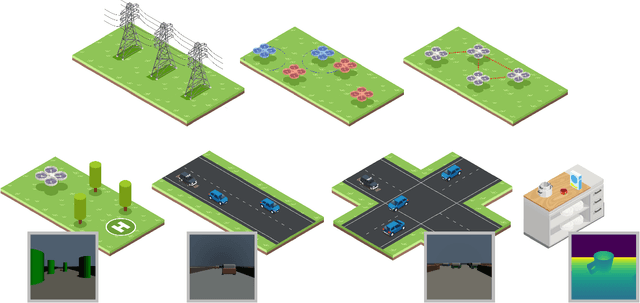
Before autonomous systems can be deployed in safety-critical applications, we must be able to understand and verify the safety of these systems. For cases where the risk or cost of real-world testing is prohibitive, we propose a simulation-based framework for a) predicting ways in which an autonomous system is likely to fail and b) automatically adjusting the system's design and control policy to preemptively mitigate those failures. Existing tools for failure prediction struggle to search over high-dimensional environmental parameters, cannot efficiently handle end-to-end testing for systems with vision in the loop, and provide little guidance on how to mitigate failures once they are discovered. We approach this problem through the lens of approximate Bayesian inference and use differentiable simulation and rendering for efficient failure case prediction and repair. For cases where a differentiable simulator is not available, we provide a gradient-free version of our algorithm, and we include a theoretical and empirical evaluation of the trade-offs between gradient-based and gradient-free methods. We apply our approach on a range of robotics and control problems, including optimizing search patterns for robot swarms, UAV formation control, and robust network control. Compared to optimization-based falsification methods, our method predicts a more diverse, representative set of failure modes, and we find that our use of differentiable simulation yields solutions that have up to 10x lower cost and requires up to 2x fewer iterations to converge relative to gradient-free techniques. In hardware experiments, we find that repairing control policies using our method leads to a 5x robustness improvement. Accompanying code and video can be found at https://mit-realm.github.io/radium/

Accelerated Algorithms for a Class of Optimization Problems with Equality and Box Constraints

Convex optimization with equality and inequality constraints is a ubiquitous problem in several optimization and control problems in large-scale systems. Recently there has been a lot of interest in establishing accelerated convergence of the loss function. A class of high-order tuners was recently proposed in an effort to lead to accelerated convergence for the case when no constraints are present. In this paper, we propose a new high-order tuner that can accommodate the presence of equality constraints. In order to accommodate the underlying box constraints, time-varying gains are introduced in the high-order tuner which leverage convexity and ensure anytime feasibility of the constraints. Numerical examples are provided to support the theoretical derivations.