Accelerated Algorithms for a Class of Optimization Problems with Equality and Box Constraints

Convex optimization with equality and inequality constraints is a ubiquitous problem in several optimization and control problems in large-scale systems. Recently there has been a lot of interest in establishing accelerated convergence of the loss function. A class of high-order tuners was recently proposed in an effort to lead to accelerated convergence for the case when no constraints are present. In this paper, we propose a new high-order tuner that can accommodate the presence of equality constraints. In order to accommodate the underlying box constraints, time-varying gains are introduced in the high-order tuner which leverage convexity and ensure anytime feasibility of the constraints. Numerical examples are provided to support the theoretical derivations.

PhML-DyR: A Physics-Informed ML framework for Dynamic Reconfiguration in Power Systems

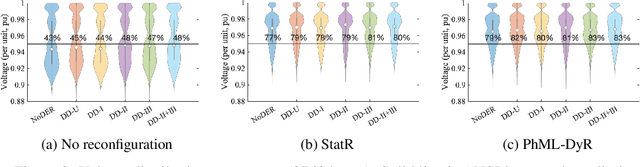
A transformation of the US electricity sector is underway with aggressive targets to achieve 100% carbon pollution-free electricity by 2035. To achieve this objective while maintaining a safe and reliable power grid, new operating paradigms are needed, of computationally fast and accurate decision making in a dynamic and uncertain environment. We propose a novel physics-informed machine learning framework for the decision of dynamic grid reconfiguration (PhML-DyR), a key task in power systems. Dynamic reconfiguration (DyR) is a process by which switch-states are dynamically set so as to lead to an optimal grid topology that minimizes line losses. To address the underlying computational complexities of NP-hardness due to the mixed nature of the decision variables, we propose the use of physics-informed ML (PhML) which integrates both operating constraints and topological and connectivity constraints into a neural network framework. Our PhML approach learns to simultaneously optimize grid topology and generator dispatch to meet loads, increase efficiency, and remain within safe operating limits. We demonstrate the effectiveness of PhML-DyR on a canonical grid, showing a reduction in electricity loss by 23%, and improved voltage profiles. We also show a reduction in constraint violations by an order of magnitude as well as in training time using PhML-DyR.

DER Forecast using Privacy Preserving Federated Learning

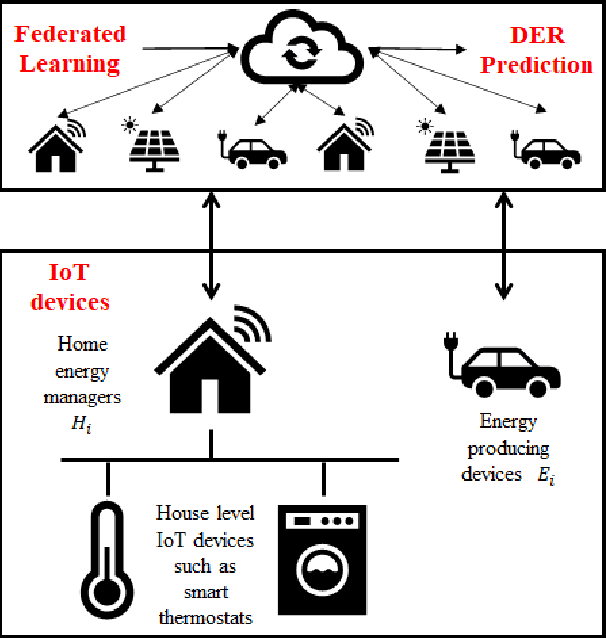
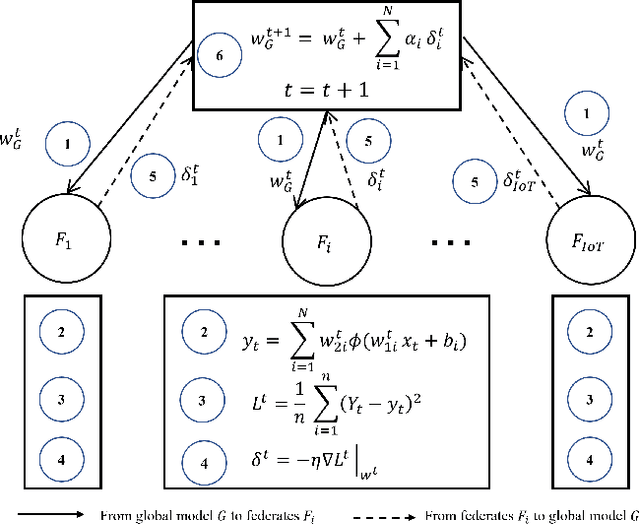
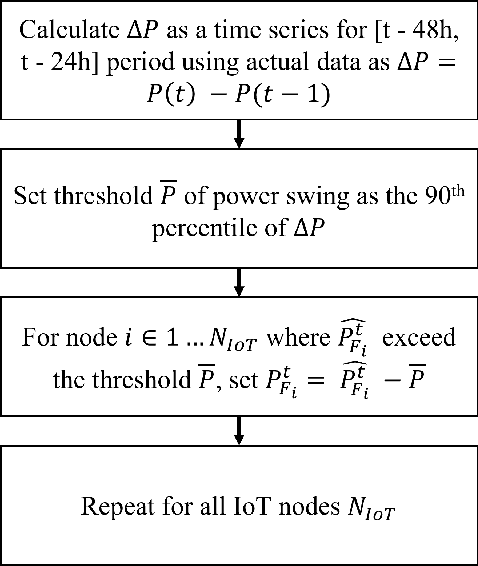
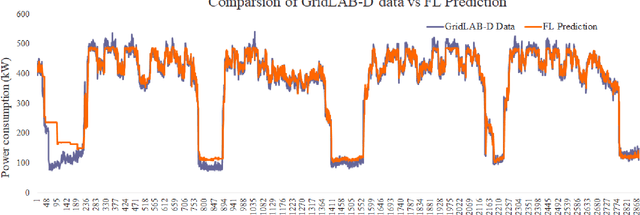
With increasing penetration of Distributed Energy Resources (DERs) in grid edge including renewable generation, flexible loads, and storage, accurate prediction of distributed generation and consumption at the consumer level becomes important. However, DER prediction based on the transmission of customer level data, either repeatedly or in large amounts, is not feasible due to privacy concerns. In this paper, a distributed machine learning approach, Federated Learning, is proposed to carry out DER forecasting using a network of IoT nodes, each of which transmits a model of the consumption and generation patterns without revealing consumer data. We consider a simulation study which includes 1000 DERs, and show that our method leads to an accurate prediction of preserve consumer privacy, while still leading to an accurate forecast. We also evaluate grid-specific performance metrics such as load swings and load curtailment and show that our FL algorithm leads to satisfactory performance. Simulations are also performed on the Pecan street dataset to demonstrate the validity of the proposed approach on real data.

Online Algorithms and Policies Using Adaptive and Machine Learning Approaches

This paper considers the problem of real-time control and learning in dynamic systems subjected to uncertainties. Adaptive approaches are proposed to address the problem, which are combined to with methods and tools in Reinforcement Learning (RL) and Machine Learning (ML). Algorithms are proposed in continuous-time that combine adaptive approaches with RL leading to online control policies that guarantee stable behavior in the presence of parametric uncertainties that occur in real-time. Algorithms are proposed in discrete-time that combine adaptive approaches proposed for parameter and output estimation and ML approaches proposed for accelerated performance that guarantee stable estimation even in the presence of time-varying regressors, and for accelerated learning of the parameters with persistent excitation. Numerical validations of all algorithms are carried out using a quadrotor landing task on a moving platform and benchmark problems in ML. All results clearly point out the advantage of adaptive approaches for real-time control and learning.

A New Algorithm for Discrete-Time Parameter Estimation

We propose a new discrete-time adaptive algorithm for parameter estimation of a class of time-varying plants. The main contribution is the inclusion of a time-varying gain matrix in the adjustment of the parameter estimates. We show that in the presence of time-varying unknown parameters, the parameter estimation error converges uniformly to a compact set under conditions of persistent excitation, with the size of the compact set proportional to the time-variation of the unknown parameters. Under conditions of finite excitation, the convergence is asymptotic and non-uniform.

A High-order Tuner for Accelerated Learning and Control

Gradient-descent based iterative algorithms pervade a variety of problems in estimation, prediction, learning, control, and optimization. Recently iterative algorithms based on higher-order information have been explored in an attempt to lead to accelerated learning. In this paper, we explore a specific a high-order tuner that has been shown to result in stability with time-varying regressors in linearly parametrized systems, and accelerated convergence with constant regressors. We show that this tuner continues to provide bounded parameter estimates even if the gradients are corrupted by noise. Additionally, we also show that the parameter estimates converge exponentially to a compact set whose size is dependent on noise statistics. As the HT algorithms can be applied to a wide range of problems in estimation, filtering, control, and machine learning, the result obtained in this paper represents an important extension to the topic of real-time and fast decision making.

A Stable High-order Tuner for General Convex Functions

Iterative gradient-based algorithms have been increasingly applied for the training of a broad variety of machine learning models including large neural-nets. In particular, momentum-based methods, with accelerated learning guarantees, have received a lot of attention due to their provable guarantees of fast learning in certain classes of problems and multiple algorithms have been derived. However, properties for these methods hold true only for constant regressors. When time-varying regressors occur, which is commonplace in dynamic systems, many of these momentum-based methods cannot guarantee stability. Recently, a new High-order Tuner (HT) was developed and shown to have 1) stability and asymptotic convergence for time-varying regressors and 2) non-asymptotic accelerated learning guarantees for constant regressors. These results were derived for a linear regression framework producing a quadratic loss function. In this paper, we extend and discuss the results of this same HT for general convex loss functions. Through the exploitation of convexity and smoothness definitions, we establish similar stability and asymptotic convergence guarantees. Additionally we conjecture that the HT has an accelerated convergence rate. Finally, we provide numerical simulations supporting the satisfactory behavior of the HT algorithm as well as the conjecture of accelerated learning.

Parameter Estimation Bounds Based on the Theory of Spectral Lines

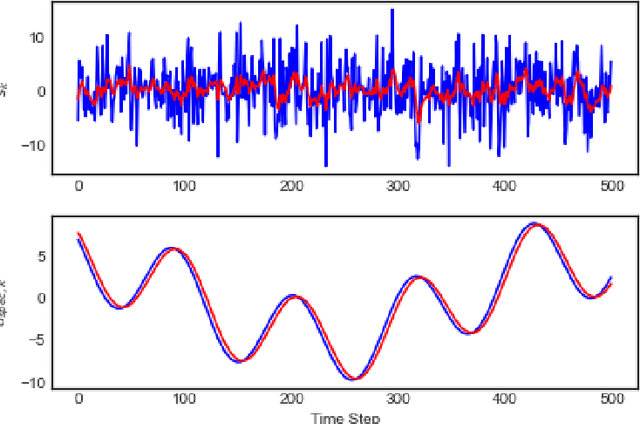
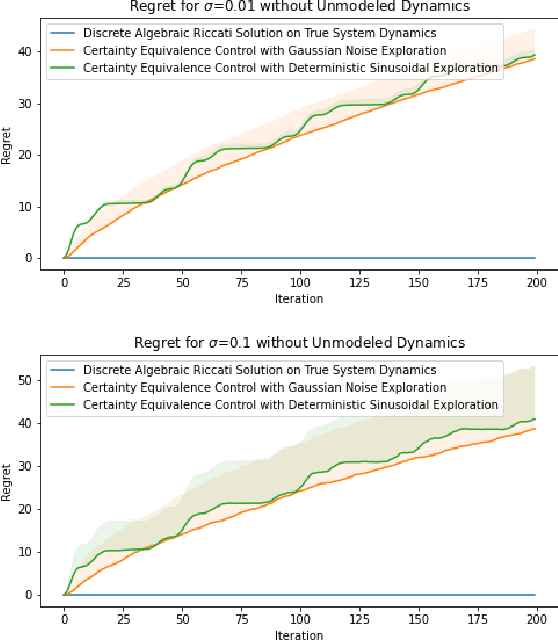
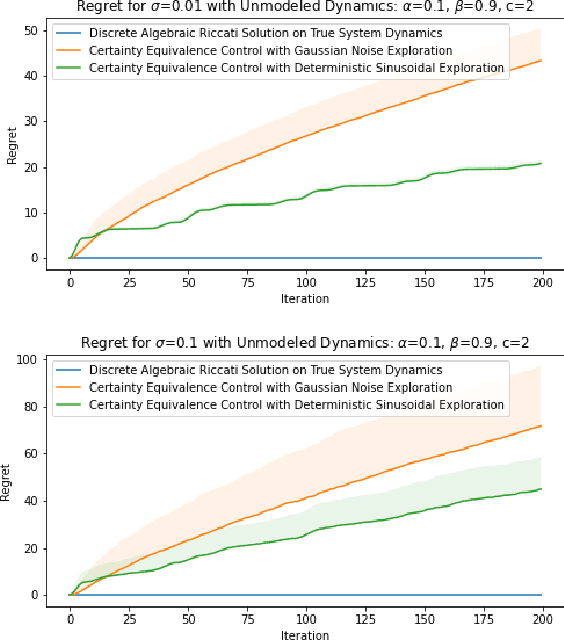
Recent methods in the machine learning literature have proposed a Gaussian noise-based exogenous signal to learn the parameters of a dynamic system. In this paper, we propose the use of a spectral lines-based deterministic exogenous signal to solve the same problem. Our theoretical analysis consists of a new toolkit which employs the theory of spectral lines, retains the stochastic setting, and leads to non-asymptotic bounds on the parameter estimation error. The results are shown to lead to a tunable parameter identification error. In particular, it is shown that the identification error can be minimized through an an optimal choice of the spectrum of the exogenous signal.

Accelerated Learning with Robustness to Adversarial Regressors

High order iterative momentum-based parameter update algorithms have seen widespread applications in training machine learning models. Recently, connections with variational approaches and continuous dynamics have led to the derivation of new classes of high order learning algorithms with accelerated learning guarantees. Such methods however, have only considered the case of static regressors. There is a significant need in continual/lifelong learning applications for parameter update algorithms which can be proven stable in the presence of adversarial time-varying regressors. In such settings, the learning algorithm must continually adapt to changes in the distribution of regressors. In this paper, we propose a new discrete time algorithm which: 1) provides stability and asymptotic convergence guarantees in the presence of adversarial regressors by leveraging insights from adaptive control theory and 2) provides non-asymptotic accelerated learning guarantees leveraging insights from convex optimization. In particular, our algorithm reaches an $\epsilon$ sub-optimal point in at most $\tilde{\mathcal{O}}(1/\sqrt{\epsilon})$ iterations when regressors are constant - matching lower bounds due to Nesterov of $\Omega(1/\sqrt{\epsilon})$, up to a $\log(1/\epsilon)$ factor and provides guaranteed bounds for stability when regressors are time-varying.

Parameter Estimation in Adaptive Control of Time-Varying Systems Under a Range of Excitation Conditions

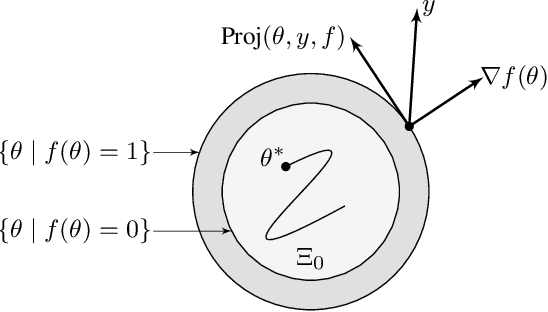
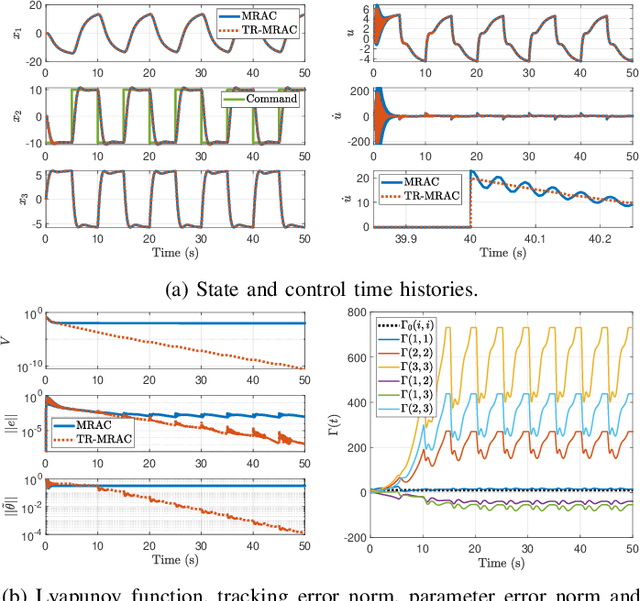
This paper presents a new parameter estimation algorithm for the adaptive control of a class of time-varying plants. The main feature of this algorithm is a matrix of time-varying learning rates, which enables parameter estimation error trajectories to tend exponentially fast towards a compact set whenever excitation conditions are satisfied. This algorithm is employed in a large class of problems where unknown parameters are present and are time-varying. It is shown that this algorithm guarantees global boundedness of the state and parameter errors of the system, and avoids an often used filtering approach for constructing key regressor signals. In addition, intervals of time over which these errors tend exponentially fast toward a compact set are provided, both in the presence of finite and persistent excitation. A projection operator is used to ensure the boundedness of the learning rate matrix, as compared to a time-varying forgetting factor. Numerical simulations are provided to complement the theoretical analysis.