Parameter Estimation in Adaptive Control of Time-Varying Systems Under a Range of Excitation Conditions
Paper and Code
Nov 10, 2019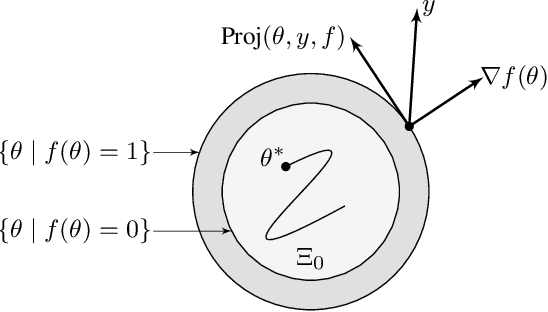
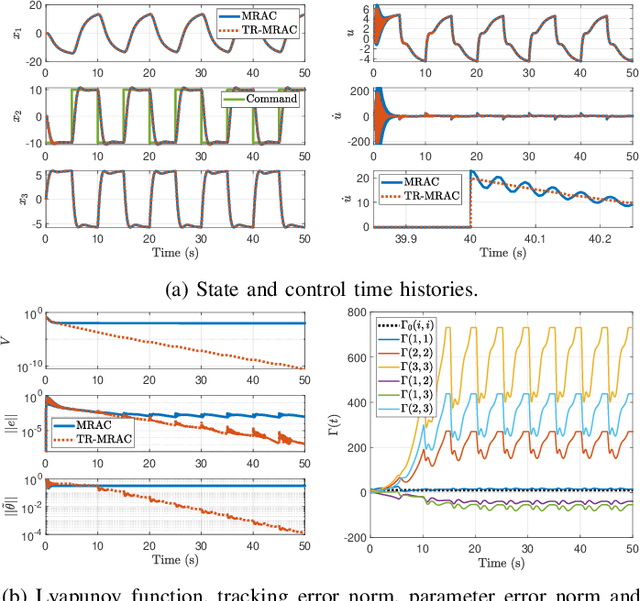


This paper presents a new parameter estimation algorithm for the adaptive control of a class of time-varying plants. The main feature of this algorithm is a matrix of time-varying learning rates, which enables parameter estimation error trajectories to tend exponentially fast towards a compact set whenever excitation conditions are satisfied. This algorithm is employed in a large class of problems where unknown parameters are present and are time-varying. It is shown that this algorithm guarantees global boundedness of the state and parameter errors of the system, and avoids an often used filtering approach for constructing key regressor signals. In addition, intervals of time over which these errors tend exponentially fast toward a compact set are provided, both in the presence of finite and persistent excitation. A projection operator is used to ensure the boundedness of the learning rate matrix, as compared to a time-varying forgetting factor. Numerical simulations are provided to complement the theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge