On the stability of second order gradient descent for time varying convex functions

Gradient based optimization algorithms deployed in Machine Learning (ML) applications are often analyzed and compared by their convergence rates or regret bounds. While these rates and bounds convey valuable information they don't always directly translate to stability guarantees. Stability and similar concepts, like robustness, will become ever more important as we move towards deploying models in real-time and safety critical systems. In this work we build upon the results in Gaudio et al. 2021 and Moreu and Annaswamy 2022 for second order gradient descent when applied to explicitly time varying cost functions and provide more general stability guarantees. These more general results can aid in the design and certification of these optimization schemes so as to help ensure safe and reliable deployment for real-time learning applications. We also hope that the techniques provided here will stimulate and cross-fertilize the analysis that occurs on the same algorithms from the online learning and stochastic optimization communities.

Online Algorithms and Policies Using Adaptive and Machine Learning Approaches

This paper considers the problem of real-time control and learning in dynamic systems subjected to uncertainties. Adaptive approaches are proposed to address the problem, which are combined to with methods and tools in Reinforcement Learning (RL) and Machine Learning (ML). Algorithms are proposed in continuous-time that combine adaptive approaches with RL leading to online control policies that guarantee stable behavior in the presence of parametric uncertainties that occur in real-time. Algorithms are proposed in discrete-time that combine adaptive approaches proposed for parameter and output estimation and ML approaches proposed for accelerated performance that guarantee stable estimation even in the presence of time-varying regressors, and for accelerated learning of the parameters with persistent excitation. Numerical validations of all algorithms are carried out using a quadrotor landing task on a moving platform and benchmark problems in ML. All results clearly point out the advantage of adaptive approaches for real-time control and learning.

A New Algorithm for Discrete-Time Parameter Estimation

We propose a new discrete-time adaptive algorithm for parameter estimation of a class of time-varying plants. The main contribution is the inclusion of a time-varying gain matrix in the adjustment of the parameter estimates. We show that in the presence of time-varying unknown parameters, the parameter estimation error converges uniformly to a compact set under conditions of persistent excitation, with the size of the compact set proportional to the time-variation of the unknown parameters. Under conditions of finite excitation, the convergence is asymptotic and non-uniform.

A High-order Tuner for Accelerated Learning and Control

Gradient-descent based iterative algorithms pervade a variety of problems in estimation, prediction, learning, control, and optimization. Recently iterative algorithms based on higher-order information have been explored in an attempt to lead to accelerated learning. In this paper, we explore a specific a high-order tuner that has been shown to result in stability with time-varying regressors in linearly parametrized systems, and accelerated convergence with constant regressors. We show that this tuner continues to provide bounded parameter estimates even if the gradients are corrupted by noise. Additionally, we also show that the parameter estimates converge exponentially to a compact set whose size is dependent on noise statistics. As the HT algorithms can be applied to a wide range of problems in estimation, filtering, control, and machine learning, the result obtained in this paper represents an important extension to the topic of real-time and fast decision making.

Parameter Estimation Bounds Based on the Theory of Spectral Lines

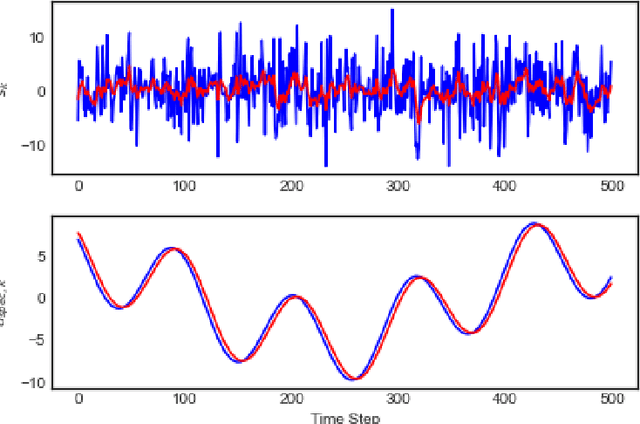
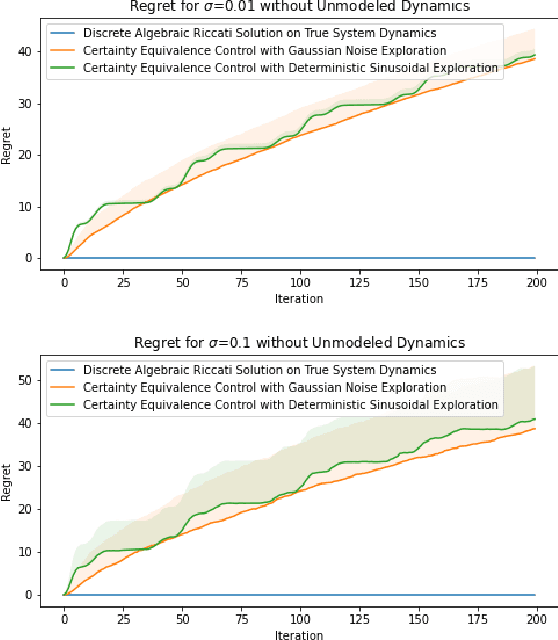
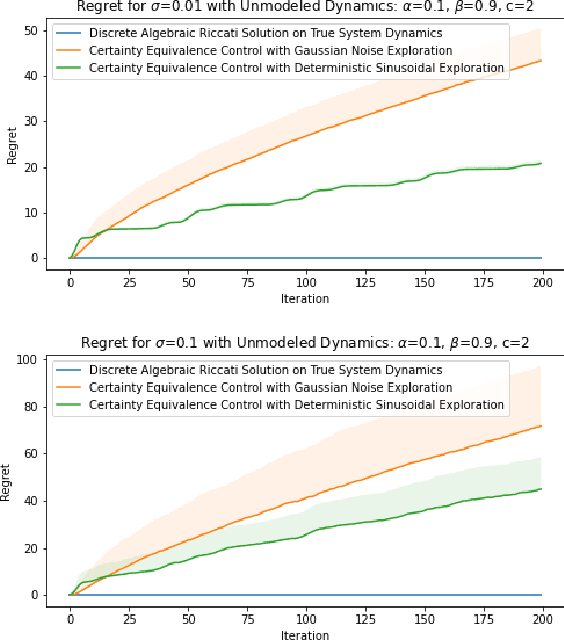
Recent methods in the machine learning literature have proposed a Gaussian noise-based exogenous signal to learn the parameters of a dynamic system. In this paper, we propose the use of a spectral lines-based deterministic exogenous signal to solve the same problem. Our theoretical analysis consists of a new toolkit which employs the theory of spectral lines, retains the stochastic setting, and leads to non-asymptotic bounds on the parameter estimation error. The results are shown to lead to a tunable parameter identification error. In particular, it is shown that the identification error can be minimized through an an optimal choice of the spectrum of the exogenous signal.

Accelerated Learning with Robustness to Adversarial Regressors

High order iterative momentum-based parameter update algorithms have seen widespread applications in training machine learning models. Recently, connections with variational approaches and continuous dynamics have led to the derivation of new classes of high order learning algorithms with accelerated learning guarantees. Such methods however, have only considered the case of static regressors. There is a significant need in continual/lifelong learning applications for parameter update algorithms which can be proven stable in the presence of adversarial time-varying regressors. In such settings, the learning algorithm must continually adapt to changes in the distribution of regressors. In this paper, we propose a new discrete time algorithm which: 1) provides stability and asymptotic convergence guarantees in the presence of adversarial regressors by leveraging insights from adaptive control theory and 2) provides non-asymptotic accelerated learning guarantees leveraging insights from convex optimization. In particular, our algorithm reaches an $\epsilon$ sub-optimal point in at most $\tilde{\mathcal{O}}(1/\sqrt{\epsilon})$ iterations when regressors are constant - matching lower bounds due to Nesterov of $\Omega(1/\sqrt{\epsilon})$, up to a $\log(1/\epsilon)$ factor and provides guaranteed bounds for stability when regressors are time-varying.

Parameter Estimation in Adaptive Control of Time-Varying Systems Under a Range of Excitation Conditions

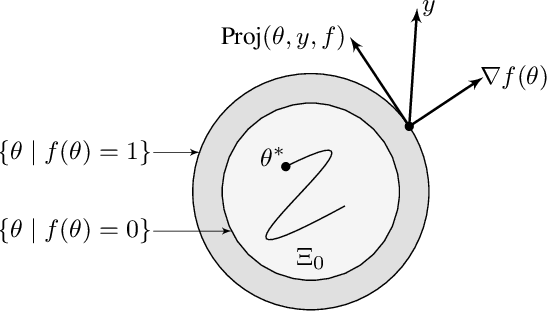
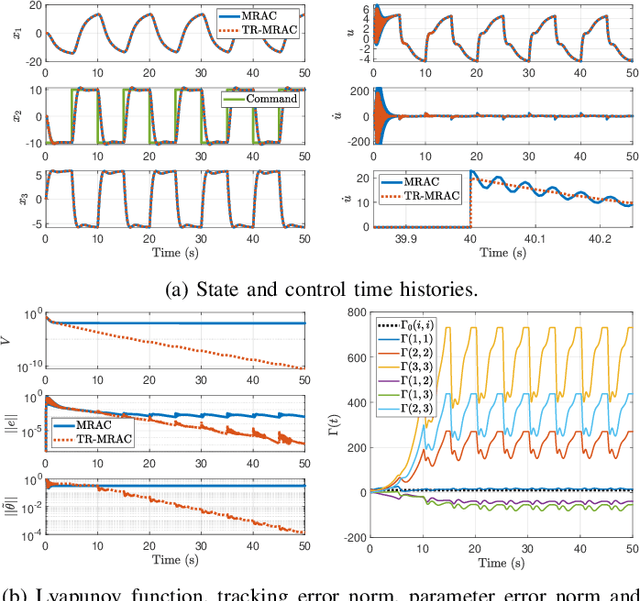
This paper presents a new parameter estimation algorithm for the adaptive control of a class of time-varying plants. The main feature of this algorithm is a matrix of time-varying learning rates, which enables parameter estimation error trajectories to tend exponentially fast towards a compact set whenever excitation conditions are satisfied. This algorithm is employed in a large class of problems where unknown parameters are present and are time-varying. It is shown that this algorithm guarantees global boundedness of the state and parameter errors of the system, and avoids an often used filtering approach for constructing key regressor signals. In addition, intervals of time over which these errors tend exponentially fast toward a compact set are provided, both in the presence of finite and persistent excitation. A projection operator is used to ensure the boundedness of the learning rate matrix, as compared to a time-varying forgetting factor. Numerical simulations are provided to complement the theoretical analysis.

Connections Between Adaptive Control and Optimization in Machine Learning

This paper demonstrates many immediate connections between adaptive control and optimization methods commonly employed in machine learning. Starting from common output error formulations, similarities in update law modifications are examined. Concepts in stability, performance, and learning, common to both fields are then discussed. Building on the similarities in update laws and common concepts, new intersections and opportunities for improved algorithm analysis are provided. In particular, a specific problem related to higher order learning is solved through insights obtained from these intersections.

Accelerated Learning in the Presence of Time Varying Features with Applications to Machine Learning and Adaptive Control

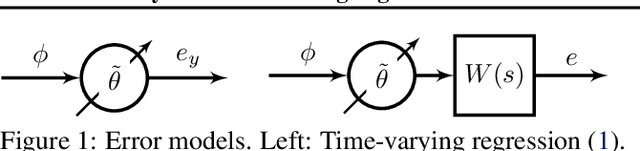
Features in machine learning problems are often time varying and may be related to outputs in an algebraic or dynamical manner. The dynamic nature of these machine learning problems renders current accelerated gradient descent methods unstable or weakens their convergence guarantees. This paper proposes algorithms for the case when time varying features are present, and demonstrates provable performance guarantees. We develop a variational perspective within a continuous time algorithm. This variational perspective includes, among other things, higher-order learning concepts and normalization, both of which stem from adaptive control, and allows stability to be established for dynamical machine learning problems. These higher-order algorithms are also examined for achieving accelerated learning in adaptive control. Simulations are provided to verify the theoretical results.