Unifying Epidemic Models with Mixtures

The COVID-19 pandemic has emphasized the need for a robust understanding of epidemic models. Current models of epidemics are classified as either mechanistic or non-mechanistic: mechanistic models make explicit assumptions on the dynamics of disease, whereas non-mechanistic models make assumptions on the form of observed time series. Here, we introduce a simple mixture-based model which bridges the two approaches while retaining benefits of both. The model represents time series of cases and fatalities as a mixture of Gaussian curves, providing a flexible function class to learn from data compared to traditional mechanistic models. Although the model is non-mechanistic, we show that it arises as the natural outcome of a stochastic process based on a networked SIR framework. This allows learned parameters to take on a more meaningful interpretation compared to similar non-mechanistic models, and we validate the interpretations using auxiliary mobility data collected during the COVID-19 pandemic. We provide a simple learning algorithm to identify model parameters and establish theoretical results which show the model can be efficiently learned from data. Empirically, we find the model to have low prediction error. The model is available live at covidpredictions.mit.edu. Ultimately, this allows us to systematically understand the impacts of interventions on COVID-19, which is critical in developing data-driven solutions to controlling epidemics.

Parameter Estimation Bounds Based on the Theory of Spectral Lines

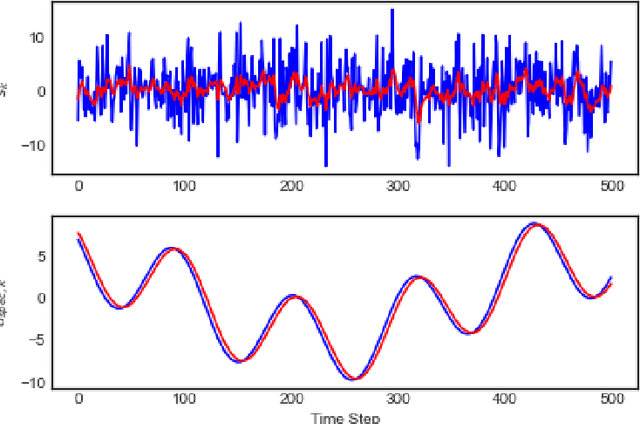
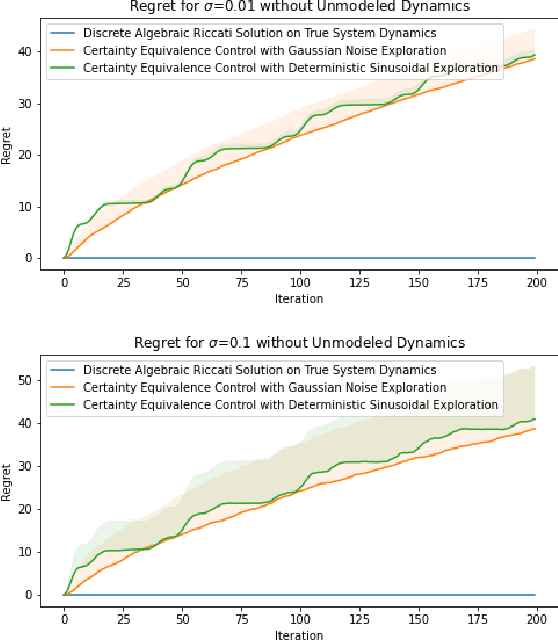
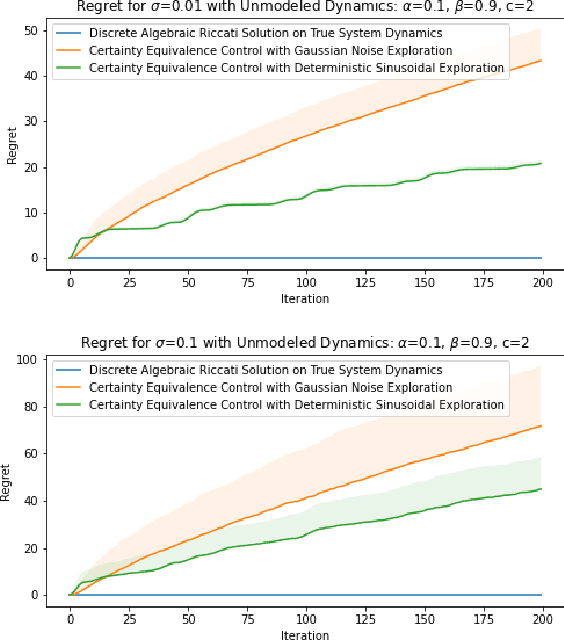
Recent methods in the machine learning literature have proposed a Gaussian noise-based exogenous signal to learn the parameters of a dynamic system. In this paper, we propose the use of a spectral lines-based deterministic exogenous signal to solve the same problem. Our theoretical analysis consists of a new toolkit which employs the theory of spectral lines, retains the stochastic setting, and leads to non-asymptotic bounds on the parameter estimation error. The results are shown to lead to a tunable parameter identification error. In particular, it is shown that the identification error can be minimized through an an optimal choice of the spectrum of the exogenous signal.

Two Burning Questions on COVID-19: Did shutting down the economy help? Can we reopen the economy without risking the second wave?

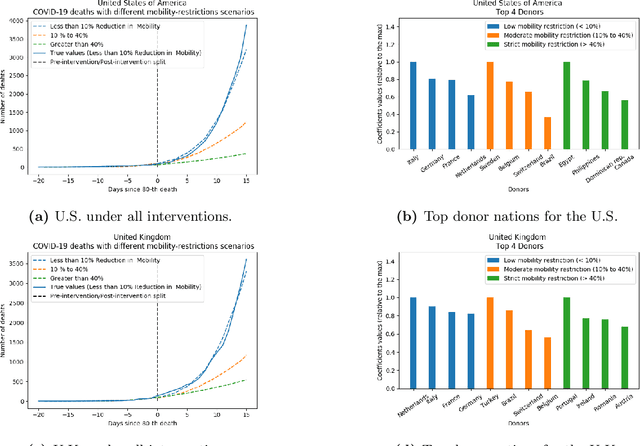
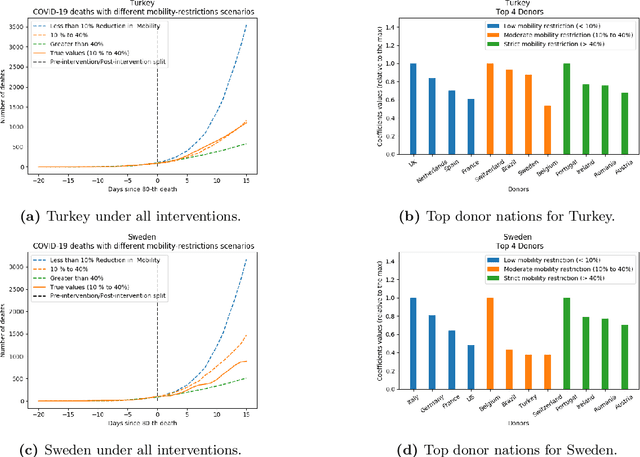
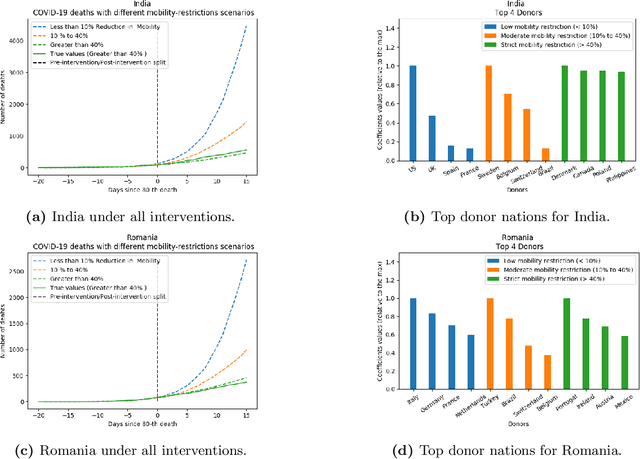
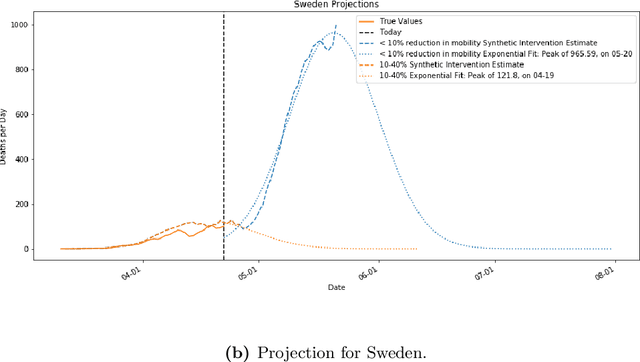
As we reach the apex of the COVID-19 pandemic, the most pressing question facing us is: can we even partially reopen the economy without risking a second wave? We first need to understand if shutting down the economy helped. And if it did, is it possible to achieve similar gains in the war against the pandemic while partially opening up the economy? To do so, it is critical to understand the effects of the various interventions that can be put into place and their corresponding health and economic implications. Since many interventions exist, the key challenge facing policy makers is understanding the potential trade-offs between them, and choosing the particular set of interventions that works best for their circumstance. In this memo, we provide an overview of Synthetic Interventions (a natural generalization of Synthetic Control), a data-driven and statistically principled method to perform what-if scenario planning, i.e., for policy makers to understand the trade-offs between different interventions before having to actually enact them. In essence, the method leverages information from different interventions that have already been enacted across the world and fits it to a policy maker's setting of interest, e.g., to estimate the effect of mobility-restricting interventions on the U.S., we use daily death data from countries that enforced severe mobility restrictions to create a "synthetic low mobility U.S." and predict the counterfactual trajectory of the U.S. if it had indeed applied a similar intervention. Using Synthetic Interventions, we find that lifting severe mobility restrictions and only retaining moderate mobility restrictions (at retail and transit locations), seems to effectively flatten the curve. We hope this provides guidance on weighing the trade-offs between the safety of the population, strain on the healthcare system, and impact on the economy.