Abdullah Alomar
Direct Alignment with Heterogeneous Preferences
Feb 22, 2025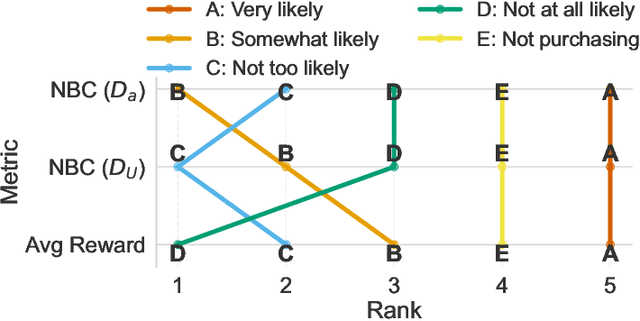

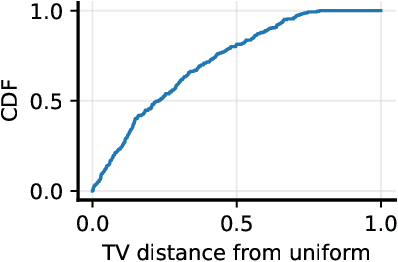
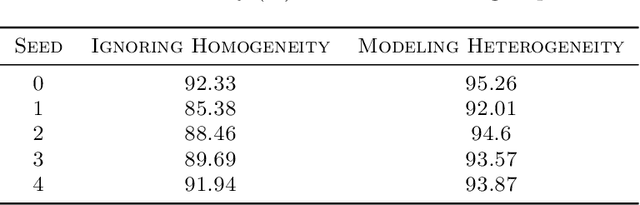
Abstract:Alignment with human preferences is commonly framed using a universal reward function, even though human preferences are inherently heterogeneous. We formalize this heterogeneity by introducing user types and examine the limits of the homogeneity assumption. We show that aligning to heterogeneous preferences with a single policy is best achieved using the average reward across user types. However, this requires additional information about annotators. We examine improvements under different information settings, focusing on direct alignment methods. We find that minimal information can yield first-order improvements, while full feedback from each user type leads to consistent learning of the optimal policy. Surprisingly, however, no sample-efficient consistent direct loss exists in this latter setting. These results reveal a fundamental tension between consistency and sample efficiency in direct policy alignment.
SAMoSSA: Multivariate Singular Spectrum Analysis with Stochastic Autoregressive Noise
May 25, 2023



Abstract:The well-established practice of time series analysis involves estimating deterministic, non-stationary trend and seasonality components followed by learning the residual stochastic, stationary components. Recently, it has been shown that one can learn the deterministic non-stationary components accurately using multivariate Singular Spectrum Analysis (mSSA) in the absence of a correlated stationary component; meanwhile, in the absence of deterministic non-stationary components, the Autoregressive (AR) stationary component can also be learnt readily, e.g. via Ordinary Least Squares (OLS). However, a theoretical underpinning of multi-stage learning algorithms involving both deterministic and stationary components has been absent in the literature despite its pervasiveness. We resolve this open question by establishing desirable theoretical guarantees for a natural two-stage algorithm, where mSSA is first applied to estimate the non-stationary components despite the presence of a correlated stationary AR component, which is subsequently learned from the residual time series. We provide a finite-sample forecasting consistency bound for the proposed algorithm, SAMoSSA, which is data-driven and thus requires minimal parameter tuning. To establish theoretical guarantees, we overcome three hurdles: (i) we characterize the spectra of Page matrices of stable AR processes, thus extending the analysis of mSSA; (ii) we extend the analysis of AR process identification in the presence of arbitrary bounded perturbations; (iii) we characterize the out-of-sample or forecasting error, as opposed to solely considering model identification. Through representative empirical studies, we validate the superior performance of SAMoSSA compared to existing baselines. Notably, SAMoSSA's ability to account for AR noise structure yields improvements ranging from 5% to 37% across various benchmark datasets.
CausalSim: Toward a Causal Data-Driven Simulator for Network Protocols
Jan 05, 2022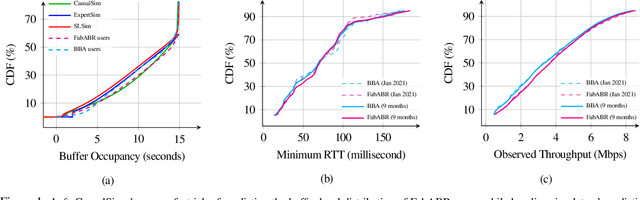
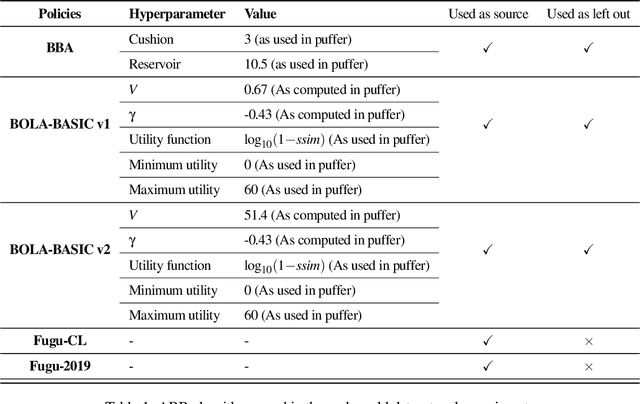
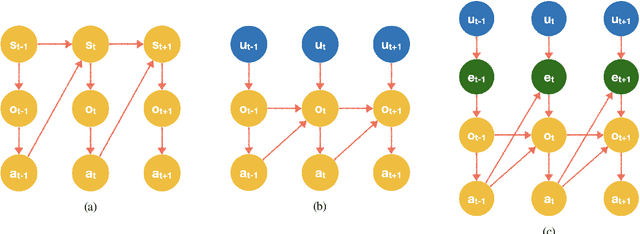
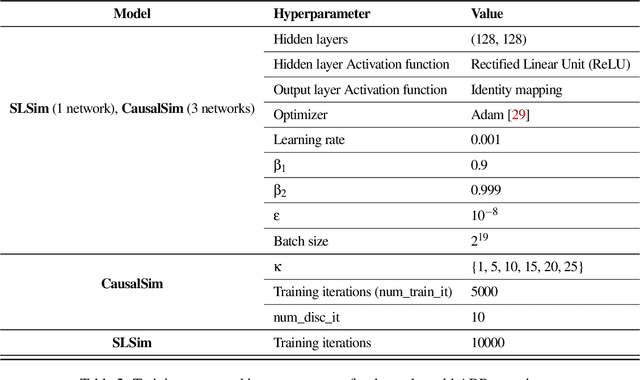
Abstract:Evaluating the real-world performance of network protocols is challenging. Randomized control trials (RCT) are expensive and inaccessible to most researchers, while expert-designed simulators fail to capture complex behaviors in real networks. We present CausalSim, a data-driven simulator for network protocols that addresses this challenge. Learning network behavior from observational data is complicated due to the bias introduced by the protocols used during data collection. CausalSim uses traces from an initial RCT under a set of protocols to learn a causal network model, effectively removing the biases present in the data. Using this model, CausalSim can then simulate any protocol over the same traces (i.e., for counterfactual predictions). Key to CausalSim is the novel use of adversarial neural network training that exploits distributional invariances that are present due to the training data coming from an RCT. Our extensive evaluation of CausalSim on both real and synthetic datasets and two use cases, including more than nine months of real data from the Puffer video streaming system, shows that it provides accurate counterfactual predictions, reducing prediction error by 44% and 53% on average compared to expert-designed and standard supervised learning baselines.
PerSim: Data-Efficient Offline Reinforcement Learning with Heterogeneous Agents via Personalized Simulators
Mar 17, 2021

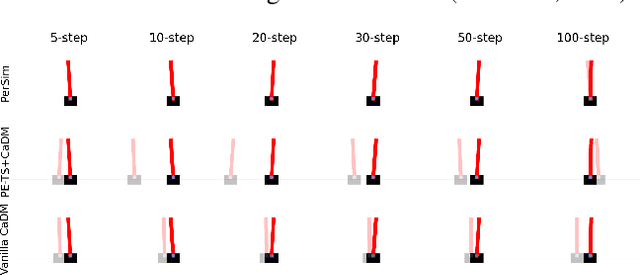
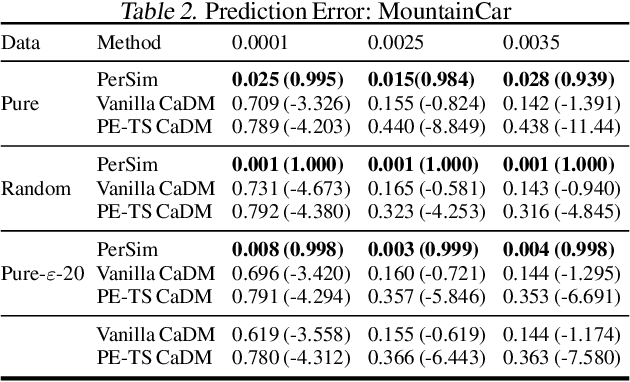
Abstract:We consider offline reinforcement learning (RL) with heterogeneous agents under severe data scarcity, i.e., we only observe a single historical trajectory for every agent under an unknown, potentially sub-optimal policy. We find that the performance of state-of-the-art offline and model-based RL methods degrade significantly given such limited data availability, even for commonly perceived "solved" benchmark settings such as "MountainCar" and "CartPole". To address this challenge, we propose a model-based offline RL approach, called PerSim, where we first learn a personalized simulator for each agent by collectively using the historical trajectories across all agents prior to learning a policy. We do so by positing that the transition dynamics across agents can be represented as a latent function of latent factors associated with agents, states, and actions; subsequently, we theoretically establish that this function is well-approximated by a "low-rank" decomposition of separable agent, state, and action latent functions. This representation suggests a simple, regularized neural network architecture to effectively learn the transition dynamics per agent, even with scarce, offline data.We perform extensive experiments across several benchmark environments and RL methods. The consistent improvement of our approach, measured in terms of state dynamics prediction and eventual reward, confirms the efficacy of our framework in leveraging limited historical data to simultaneously learn personalized policies across agents.
On Multivariate Singular Spectrum Analysis
Jun 24, 2020



Abstract:We analyze a variant of multivariate singular spectrum analysis (mSSA), a widely used multivariate time series method, which we find to perform competitively with respect to the state-of-art neural network time series methods (LSTM, DeepAR). Its restriction for single time series, singular spectrum analysis (SSA), has been analyzed recently. Despite its popularity, theoretical understanding of mSSA is absent. Towards this, we introduce a natural spatio-temporal factor model to analyze mSSA. We establish the in-sample prediction error for imputation and forecasting under mSSA scales as $1/\sqrt{NT}$, for $N$ time series with $T$ observations per time series. In contrast, for SSA the error scales as $1/\sqrt{T}$ and for matrix factorization based time series methods, the error scales as ${1}/{\min(N, T)}$. We utilize an online learning framework to analyze the one-step-ahead prediction error of mSSA and establish it has a regret of ${1}/{(\sqrt{N}T^{0.04})}$ with respect to in-sample forecasting error. By applying mSSA on the square of the time series observations, we furnish an algorithm to estimate the time-varying variance of a time series and establish it has in-sample imputation / forecasting error scaling as $1/\sqrt{NT}$. To establish our results, we make three technical contributions. First, we establish that the "stacked" Page Matrix time series representation, the core data structure in mSSA, has an approximate low-rank structure for a large class of time series models used in practice under the spatio-temporal factor model. Second, we extend the theory of online convex optimization to address the variant when the constraints are time-varying. Third, we extend the analysis prediction error analysis of Principle Component Regression beyond recent work to when the covariate matrix is approximately low-rank.
Synthetic Interventions
Jun 13, 2020
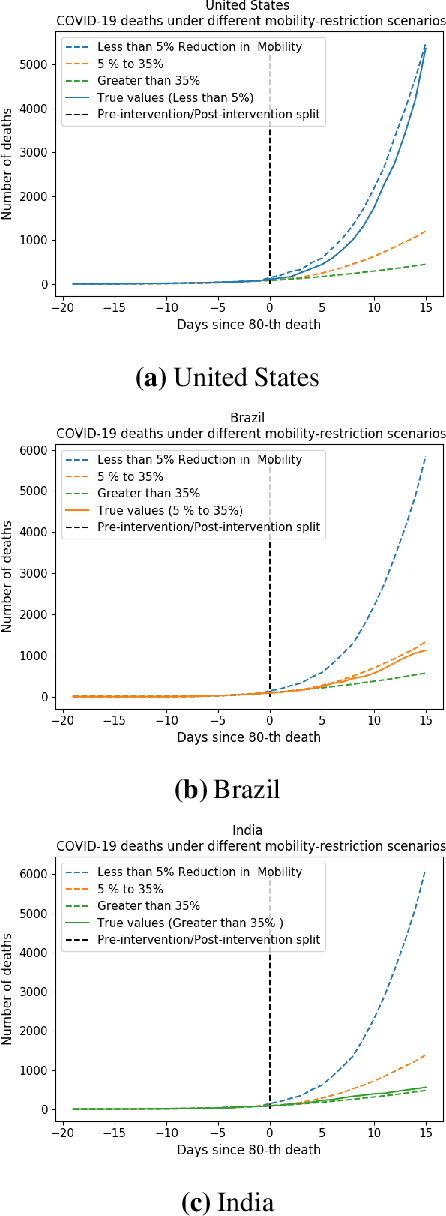


Abstract:We develop a method to help quantify the impact different levels of mobility restrictions could have had on COVID-19 related deaths across nations. Synthetic control (SC) has emerged as a standard tool in such scenarios to produce counterfactual estimates if a particular intervention had not occurred, using just observational data. However, it remains an important open problem of how to extend SC to obtain counterfactual estimates if a particular intervention had occurred - this is exactly the question of the impact of mobility restrictions stated above. As our main contribution, we introduce synthetic interventions (SI), which helps resolve this open problem by allowing one to produce counterfactual estimates if there are multiple interventions of interest. We prove SI produces consistent counterfactual estimates under a tensor factor model. Our finite sample analysis shows the test error decays as $1/T_0$, where $T_0$ is the amount of observed pre-intervention data. As a special case, this improves upon the $1/\sqrt{T_0}$ bound on test error for SC in prior works. Our test error bound holds under a certain "subspace inclusion" condition; we furnish a data-driven hypothesis test with provable guarantees to check for this condition. This also provides a quantitative hypothesis test for when to use SC, currently absent in the literature. Technically, we establish the parameter estimation and test error for Principal Component Regression (a key subroutine in SI and several SC variants) under the setting of error-in-variable regression decays as $1/T_0$, where $T_0$ is the number of samples observed; this improves the best prior test error bound of $1/\sqrt{T_0}$. In addition to the COVID-19 case study, we show how SI can be used to run data-efficient, personalized randomized control trials using real data from a large e-commerce website and a large developmental economics study.
Two Burning Questions on COVID-19: Did shutting down the economy help? Can we reopen the economy without risking the second wave?
May 10, 2020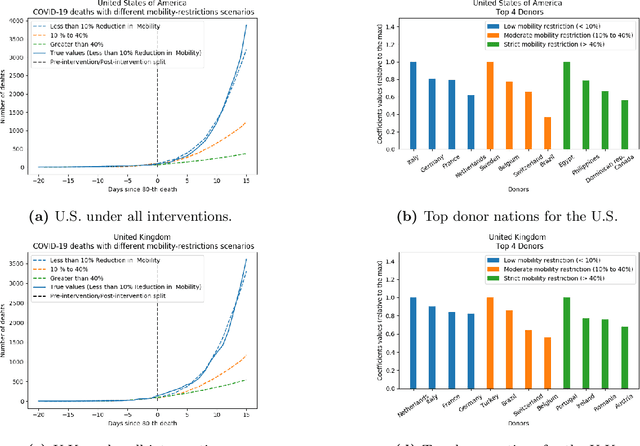
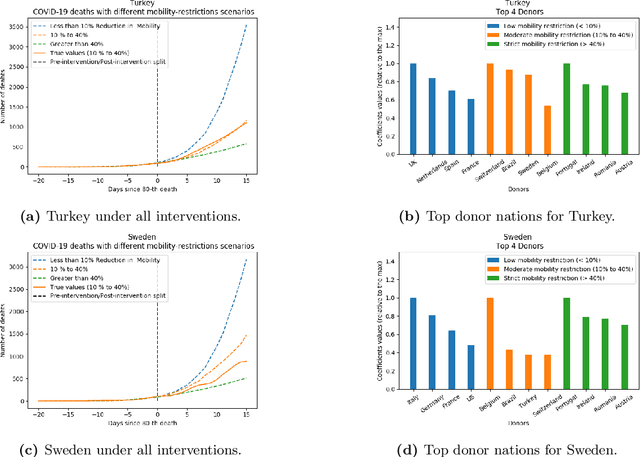
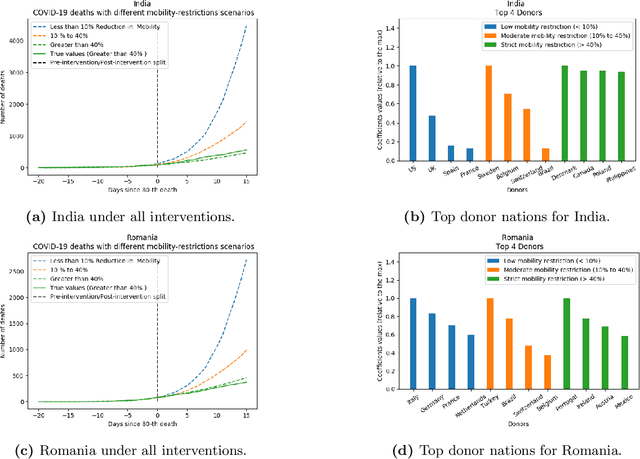
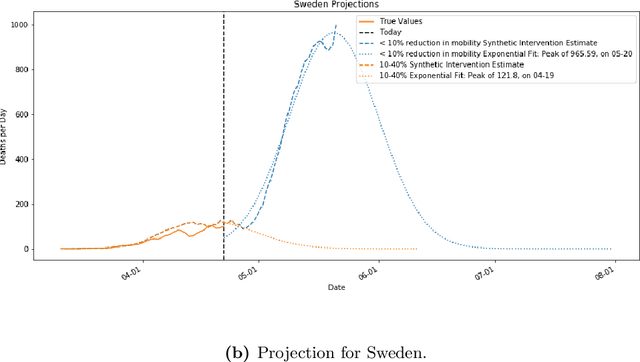
Abstract:As we reach the apex of the COVID-19 pandemic, the most pressing question facing us is: can we even partially reopen the economy without risking a second wave? We first need to understand if shutting down the economy helped. And if it did, is it possible to achieve similar gains in the war against the pandemic while partially opening up the economy? To do so, it is critical to understand the effects of the various interventions that can be put into place and their corresponding health and economic implications. Since many interventions exist, the key challenge facing policy makers is understanding the potential trade-offs between them, and choosing the particular set of interventions that works best for their circumstance. In this memo, we provide an overview of Synthetic Interventions (a natural generalization of Synthetic Control), a data-driven and statistically principled method to perform what-if scenario planning, i.e., for policy makers to understand the trade-offs between different interventions before having to actually enact them. In essence, the method leverages information from different interventions that have already been enacted across the world and fits it to a policy maker's setting of interest, e.g., to estimate the effect of mobility-restricting interventions on the U.S., we use daily death data from countries that enforced severe mobility restrictions to create a "synthetic low mobility U.S." and predict the counterfactual trajectory of the U.S. if it had indeed applied a similar intervention. Using Synthetic Interventions, we find that lifting severe mobility restrictions and only retaining moderate mobility restrictions (at retail and transit locations), seems to effectively flatten the curve. We hope this provides guidance on weighing the trade-offs between the safety of the population, strain on the healthcare system, and impact on the economy.
Time Series Predict DB
Mar 17, 2019



Abstract:In this work, we are motivated to make predictive functionalities native to database systems with focus on time series data. We propose a system architecture, Time Series Predict DB, that enables predictive query in any existing time series database by building an additional "prediction index" for time series data. To be effective, such an index needs to be built incrementally while keeping up with database throughput, able to scale with volume of data, provide accurate predictions for heterogeneous data, and allow for "predictive" querying with latency comparable to the traditional database queries. Building upon a recently developed model agnostic time series algorithm by making it incremental and scalable, we build such a system on top of PostgreSQL. Using extensive experimentation, we show that our incremental prediction index updates faster than PostgreSQL ($1\mu s$ per data for prediction index vs $4\mu s$ per data for PostgreSQL) and thus not affecting the throughput of the database. Across a variety of time series data, we find? that our incremental, model agnostic algorithm provides better accuracy compared to the best state-of-art time series libraries (median improvement in range 3.29 to 4.19x over Prophet of Facebook, 1.27 to 1.48x over AMELIA in R). The latency of predictive queries with respect to SELECT queries (0.5ms) is < 1.9x (0.8ms) for imputation and < 7.6x (3ms) for forecasting across machine platforms. As a by-product, we find that the incremental, scalable variant we propose improves the accuracy of the batch prediction algorithm which may be of interest in its own right.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge