Exploiting Observation Bias to Improve Matrix Completion

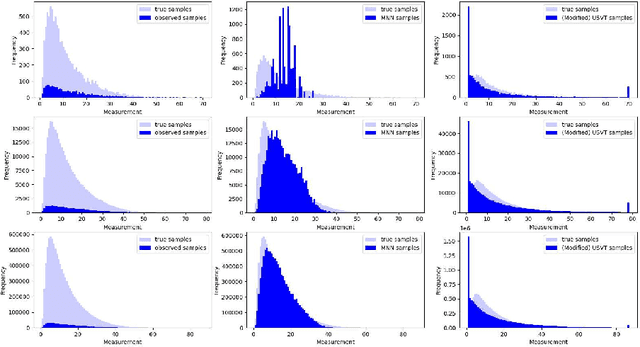
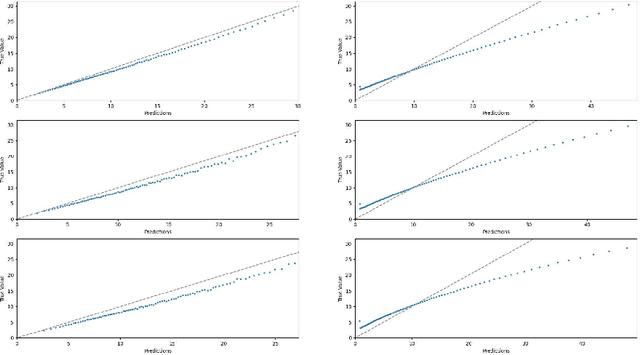
We consider a variant of matrix completion where entries are revealed in a biased manner, adopting a model akin to that introduced by Ma and Chen. Instead of treating this observation bias as a disadvantage, as is typically the case, our goal is to exploit the shared information between the bias and the outcome of interest to improve predictions. Towards this, we propose a simple two-stage algorithm: (i) interpreting the observation pattern as a fully observed noisy matrix, we apply traditional matrix completion methods to the observation pattern to estimate the distances between the latent factors; (ii) we apply supervised learning on the recovered features to impute missing observations. We establish finite-sample error rates that are competitive with the corresponding supervised learning parametric rates, suggesting that our learning performance is comparable to having access to the unobserved covariates. Empirical evaluation using a real-world dataset reflects similar performance gains, with our algorithm's estimates having 30x smaller mean squared error compared to traditional matrix completion methods.

SAMoSSA: Multivariate Singular Spectrum Analysis with Stochastic Autoregressive Noise

The well-established practice of time series analysis involves estimating deterministic, non-stationary trend and seasonality components followed by learning the residual stochastic, stationary components. Recently, it has been shown that one can learn the deterministic non-stationary components accurately using multivariate Singular Spectrum Analysis (mSSA) in the absence of a correlated stationary component; meanwhile, in the absence of deterministic non-stationary components, the Autoregressive (AR) stationary component can also be learnt readily, e.g. via Ordinary Least Squares (OLS). However, a theoretical underpinning of multi-stage learning algorithms involving both deterministic and stationary components has been absent in the literature despite its pervasiveness. We resolve this open question by establishing desirable theoretical guarantees for a natural two-stage algorithm, where mSSA is first applied to estimate the non-stationary components despite the presence of a correlated stationary AR component, which is subsequently learned from the residual time series. We provide a finite-sample forecasting consistency bound for the proposed algorithm, SAMoSSA, which is data-driven and thus requires minimal parameter tuning. To establish theoretical guarantees, we overcome three hurdles: (i) we characterize the spectra of Page matrices of stable AR processes, thus extending the analysis of mSSA; (ii) we extend the analysis of AR process identification in the presence of arbitrary bounded perturbations; (iii) we characterize the out-of-sample or forecasting error, as opposed to solely considering model identification. Through representative empirical studies, we validate the superior performance of SAMoSSA compared to existing baselines. Notably, SAMoSSA's ability to account for AR noise structure yields improvements ranging from 5% to 37% across various benchmark datasets.