Distributional Matrix Completion via Nearest Neighbors in the Wasserstein Space

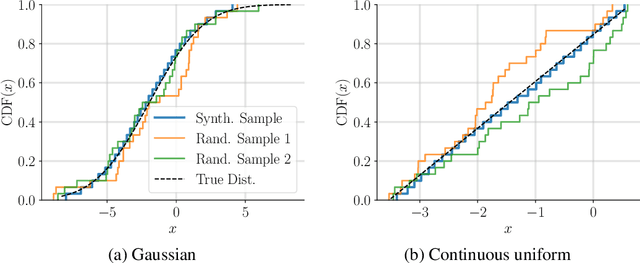
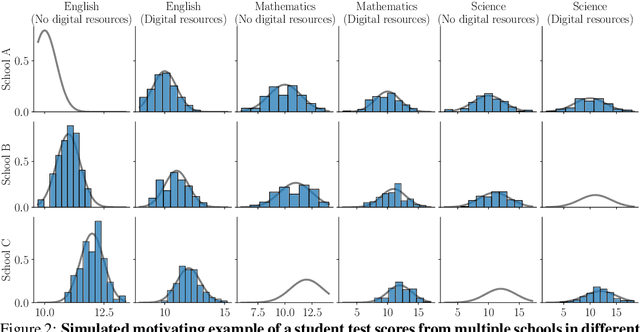
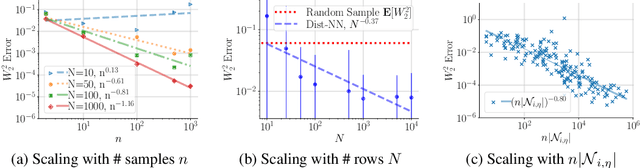
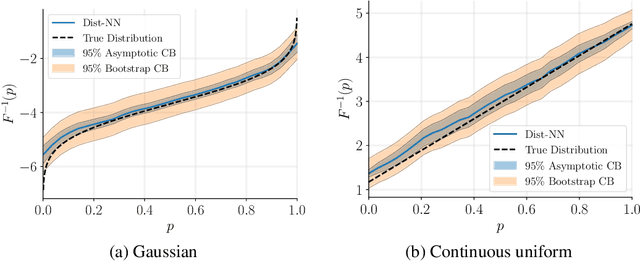
We introduce the problem of distributional matrix completion: Given a sparsely observed matrix of empirical distributions, we seek to impute the true distributions associated with both observed and unobserved matrix entries. This is a generalization of traditional matrix completion where the observations per matrix entry are scalar valued. To do so, we utilize tools from optimal transport to generalize the nearest neighbors method to the distributional setting. Under a suitable latent factor model on probability distributions, we establish that our method recovers the distributions in the Wasserstein norm. We demonstrate through simulations that our method is able to (i) provide better distributional estimates for an entry compared to using observed samples for that entry alone, (ii) yield accurate estimates of distributional quantities such as standard deviation and value-at-risk, and (iii) inherently support heteroscedastic noise. We also prove novel asymptotic results for Wasserstein barycenters over one-dimensional distributions.

Learning Counterfactual Distributions via Kernel Nearest Neighbors

Consider a setting with multiple units (e.g., individuals, cohorts, geographic locations) and outcomes (e.g., treatments, times, items), where the goal is to learn a multivariate distribution for each unit-outcome entry, such as the distribution of a user's weekly spend and engagement under a specific mobile app version. A common challenge is the prevalence of missing not at random data, where observations are available only for certain unit-outcome combinations and the observation availability can be correlated with the properties of distributions themselves, i.e., there is unobserved confounding. An additional challenge is that for any observed unit-outcome entry, we only have a finite number of samples from the underlying distribution. We tackle these two challenges by casting the problem into a novel distributional matrix completion framework and introduce a kernel based distributional generalization of nearest neighbors to estimate the underlying distributions. By leveraging maximum mean discrepancies and a suitable factor model on the kernel mean embeddings of the underlying distributions, we establish consistent recovery of the underlying distributions even when data is missing not at random and positivity constraints are violated. Furthermore, we demonstrate that our nearest neighbors approach is robust to heteroscedastic noise, provided we have access to two or more measurements for the observed unit-outcome entries, a robustness not present in prior works on nearest neighbors with single measurements.

Multi-Armed Bandits with Network Interference

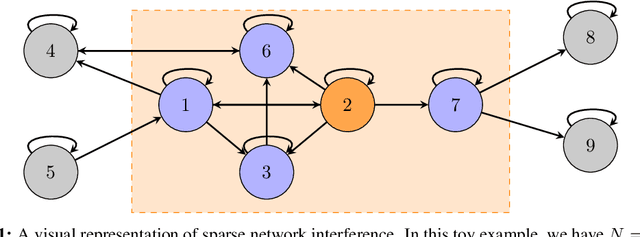
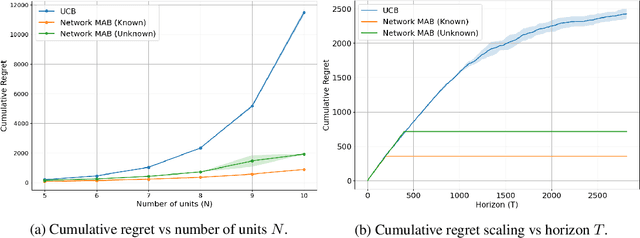
Online experimentation with interference is a common challenge in modern applications such as e-commerce and adaptive clinical trials in medicine. For example, in online marketplaces, the revenue of a good depends on discounts applied to competing goods. Statistical inference with interference is widely studied in the offline setting, but far less is known about how to adaptively assign treatments to minimize regret. We address this gap by studying a multi-armed bandit (MAB) problem where a learner (e-commerce platform) sequentially assigns one of possible $\mathcal{A}$ actions (discounts) to $N$ units (goods) over $T$ rounds to minimize regret (maximize revenue). Unlike traditional MAB problems, the reward of each unit depends on the treatments assigned to other units, i.e., there is interference across the underlying network of units. With $\mathcal{A}$ actions and $N$ units, minimizing regret is combinatorially difficult since the action space grows as $\mathcal{A}^N$. To overcome this issue, we study a sparse network interference model, where the reward of a unit is only affected by the treatments assigned to $s$ neighboring units. We use tools from discrete Fourier analysis to develop a sparse linear representation of the unit-specific reward $r_n: [\mathcal{A}]^N \rightarrow \mathbb{R} $, and propose simple, linear regression-based algorithms to minimize regret. Importantly, our algorithms achieve provably low regret both when the learner observes the interference neighborhood for all units and when it is unknown. This significantly generalizes other works on this topic which impose strict conditions on the strength of interference on a known network, and also compare regret to a markedly weaker optimal action. Empirically, we corroborate our theoretical findings via numerical simulations.

Doubly Robust Inference in Causal Latent Factor Models

This article introduces a new framework for estimating average treatment effects under unobserved confounding in modern data-rich environments featuring large numbers of units and outcomes. The proposed estimator is doubly robust, combining outcome imputation, inverse probability weighting, and a novel cross-fitting procedure for matrix completion. We derive finite-sample and asymptotic guarantees, and show that the error of the new estimator converges to a mean-zero Gaussian distribution at a parametric rate. Simulation results demonstrate the practical relevance of the formal properties of the estimators analyzed in this article.

Incentive-Aware Synthetic Control: Accurate Counterfactual Estimation via Incentivized Exploration

We consider a panel data setting in which one observes measurements of units over time, under different interventions. Our focus is on the canonical family of synthetic control methods (SCMs) which, after a pre-intervention time period when all units are under control, estimate counterfactual outcomes for test units in the post-intervention time period under control by using data from donor units who have remained under control for the entire post-intervention period. In order for the counterfactual estimate produced by synthetic control for a test unit to be accurate, there must be sufficient overlap between the outcomes of the donor units and the outcomes of the test unit. As a result, a canonical assumption in the literature on SCMs is that the outcomes for the test units lie within either the convex hull or the linear span of the outcomes for the donor units. However despite their ubiquity, such overlap assumptions may not always hold, as is the case when, e.g., units select their own interventions and different subpopulations of units prefer different interventions a priori. We shed light on this typically overlooked assumption, and we address this issue by incentivizing units with different preferences to take interventions they would not normally consider. Specifically, we provide a SCM for incentivizing exploration in panel data settings which provides incentive-compatible intervention recommendations to units by leveraging tools from information design and online learning. Using our algorithm, we show how to obtain valid counterfactual estimates using SCMs without the need for an explicit overlap assumption on the unit outcomes.

Adaptive Principal Component Regression with Applications to Panel Data

Principal component regression (PCR) is a popular technique for fixed-design error-in-variables regression, a generalization of the linear regression setting in which the observed covariates are corrupted with random noise. We provide the first time-uniform finite sample guarantees for online (regularized) PCR whenever data is collected adaptively. Since the proof techniques for analyzing PCR in the fixed design setting do not readily extend to the online setting, our results rely on adapting tools from modern martingale concentration to the error-in-variables setting. As an application of our bounds, we provide a framework for experiment design in panel data settings when interventions are assigned adaptively. Our framework may be thought of as a generalization of the synthetic control and synthetic interventions frameworks, where data is collected via an adaptive intervention assignment policy.

Estimating the Value of Evidence-Based Decision Making

Business/policy decisions are often based on evidence from randomized experiments and observational studies. In this article we propose an empirical framework to estimate the value of evidence-based decision making (EBDM) and the return on the investment in statistical precision.

Synthetic Combinations: A Causal Inference Framework for Combinatorial Interventions

We consider a setting with $N$ heterogeneous units and $p$ interventions. Our goal is to learn unit-specific potential outcomes for any combination of these $p$ interventions, i.e., $N \times 2^p$ causal parameters. Choosing combinations of interventions is a problem that naturally arises in many applications such as factorial design experiments, recommendation engines (e.g., showing a set of movies that maximizes engagement for users), combination therapies in medicine, selecting important features for ML models, etc. Running $N \times 2^p$ experiments to estimate the various parameters is infeasible as $N$ and $p$ grow. Further, with observational data there is likely confounding, i.e., whether or not a unit is seen under a combination is correlated with its potential outcome under that combination. To address these challenges, we propose a novel model that imposes latent structure across both units and combinations. We assume latent similarity across units (i.e., the potential outcomes matrix is rank $r$) and regularity in how combinations interact (i.e., the coefficients in the Fourier expansion of the potential outcomes is $s$ sparse). We establish identification for all causal parameters despite unobserved confounding. We propose an estimation procedure, Synthetic Combinations, and establish finite-sample consistency under precise conditions on the observation pattern. Our results imply Synthetic Combinations consistently estimates unit-specific potential outcomes given $\text{poly}(r) \times (N + s^2p)$ observations. In comparison, previous methods that do not exploit structure across both units and combinations have sample complexity scaling as $\min(N \times s^2p, \ \ r \times (N + 2^p))$. We use Synthetic Combinations to propose a data-efficient experimental design mechanism for combinatorial causal inference. We corroborate our theoretical findings with numerical simulations.

Strategyproof Decision-Making in Panel Data Settings and Beyond

We propose a framework for decision-making in the presence of strategic agents with panel data, a standard setting in econometrics and statistics where one gets noisy, repeated measurements of multiple units. We consider a setup where there is a pre-intervention period, when the principal observes the outcomes of each unit, after which the principal uses these observations to assign treatment to each unit. Our model can be thought of as a generalization of the synthetic controls and synthetic interventions frameworks, where units (or agents) may strategically manipulate pre-intervention outcomes to receive a more desirable intervention. We identify necessary and sufficient conditions under which a strategyproof mechanism that assigns interventions in the post-intervention period exists. Under a latent factor model assumption, we show that whenever a strategyproof mechanism exists, there is one with a simple closed form. In the setting where there is a single treatment and control (i.e., no other interventions), we establish that there is always a strategyproof mechanism, and provide an algorithm for learning such a mechanism. For the setting of multiple interventions, we provide an algorithm for learning a strategyproof mechanism, if there exists a sufficiently large gap in rewards between the different interventions. Along the way, we prove impossibility results for multi-class strategic classification, which may be of independent interest.

Network Synthetic Interventions: A Framework for Panel Data with Network Interference

We propose a generalization of the synthetic controls and synthetic interventions methodology to incorporate network interference. We consider the estimation of unit-specific treatment effects from panel data where there are spillover effects across units and in the presence of unobserved confounding. Key to our approach is a novel latent factor model that takes into account network interference and generalizes the factor models typically used in panel data settings. We propose an estimator, "network synthetic interventions", and show that it consistently estimates the mean outcomes for a unit under an arbitrary sequence of treatments for itself and its neighborhood, given certain observation patterns hold in the data. We corroborate our theoretical findings with simulations.