Multi-Armed Bandits with Network Interference

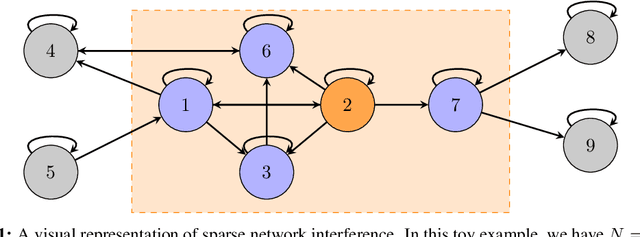
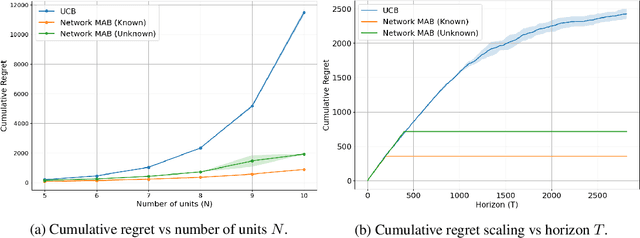
Online experimentation with interference is a common challenge in modern applications such as e-commerce and adaptive clinical trials in medicine. For example, in online marketplaces, the revenue of a good depends on discounts applied to competing goods. Statistical inference with interference is widely studied in the offline setting, but far less is known about how to adaptively assign treatments to minimize regret. We address this gap by studying a multi-armed bandit (MAB) problem where a learner (e-commerce platform) sequentially assigns one of possible $\mathcal{A}$ actions (discounts) to $N$ units (goods) over $T$ rounds to minimize regret (maximize revenue). Unlike traditional MAB problems, the reward of each unit depends on the treatments assigned to other units, i.e., there is interference across the underlying network of units. With $\mathcal{A}$ actions and $N$ units, minimizing regret is combinatorially difficult since the action space grows as $\mathcal{A}^N$. To overcome this issue, we study a sparse network interference model, where the reward of a unit is only affected by the treatments assigned to $s$ neighboring units. We use tools from discrete Fourier analysis to develop a sparse linear representation of the unit-specific reward $r_n: [\mathcal{A}]^N \rightarrow \mathbb{R} $, and propose simple, linear regression-based algorithms to minimize regret. Importantly, our algorithms achieve provably low regret both when the learner observes the interference neighborhood for all units and when it is unknown. This significantly generalizes other works on this topic which impose strict conditions on the strength of interference on a known network, and also compare regret to a markedly weaker optimal action. Empirically, we corroborate our theoretical findings via numerical simulations.

Improved prediction of future user activity in online A/B testing

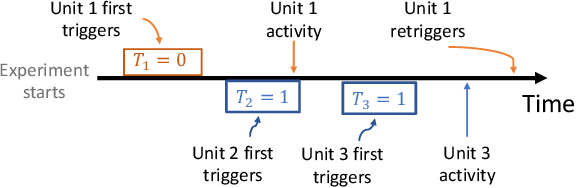
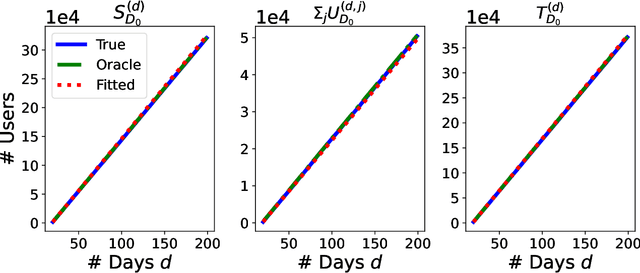
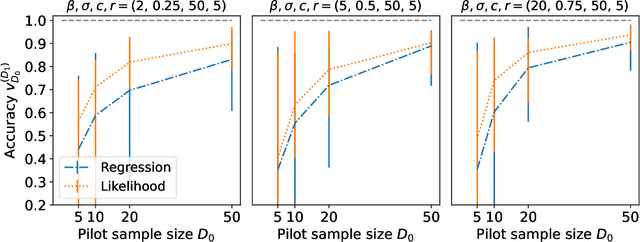
In online randomized experiments or A/B tests, accurate predictions of participant inclusion rates are of paramount importance. These predictions not only guide experimenters in optimizing the experiment's duration but also enhance the precision of treatment effect estimates. In this paper we present a novel, straightforward, and scalable Bayesian nonparametric approach for predicting the rate at which individuals will be exposed to interventions within the realm of online A/B testing. Our approach stands out by offering dual prediction capabilities: it forecasts both the quantity of new customers expected in future time windows and, unlike available alternative methods, the number of times they will be observed. We derive closed-form expressions for the posterior distributions of the quantities needed to form predictions about future user activity, thereby bypassing the need for numerical algorithms such as Markov chain Monte Carlo. After a comprehensive exposition of our model, we test its performance on experiments on real and simulated data, where we show its superior performance with respect to existing alternatives in the literature.

A Nonparametric Bayes Approach to Online Activity Prediction

Accurately predicting the onset of specific activities within defined timeframes holds significant importance in several applied contexts. In particular, accurate prediction of the number of future users that will be exposed to an intervention is an important piece of information for experimenters running online experiments (A/B tests). In this work, we propose a novel approach to predict the number of users that will be active in a given time period, as well as the temporal trajectory needed to attain a desired user participation threshold. We model user activity using a Bayesian nonparametric approach which allows us to capture the underlying heterogeneity in user engagement. We derive closed-form expressions for the number of new users expected in a given period, and a simple Monte Carlo algorithm targeting the posterior distribution of the number of days needed to attain a desired number of users; the latter is important for experimental planning. We illustrate the performance of our approach via several experiments on synthetic and real world data, in which we show that our novel method outperforms existing competitors.

Independent finite approximations for Bayesian nonparametric inference: construction, error bounds, and practical implications

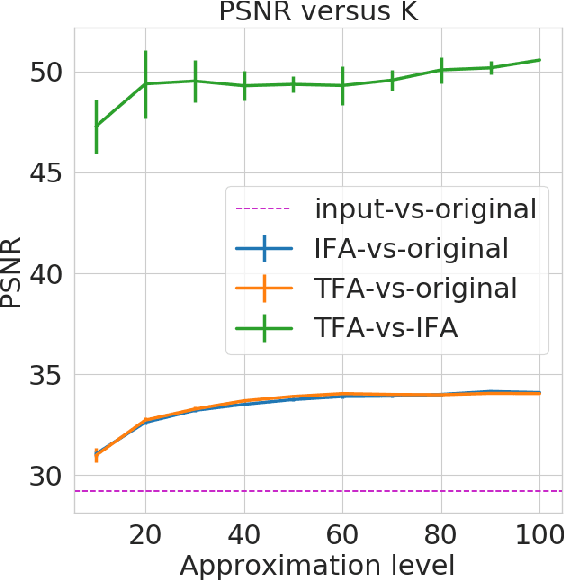
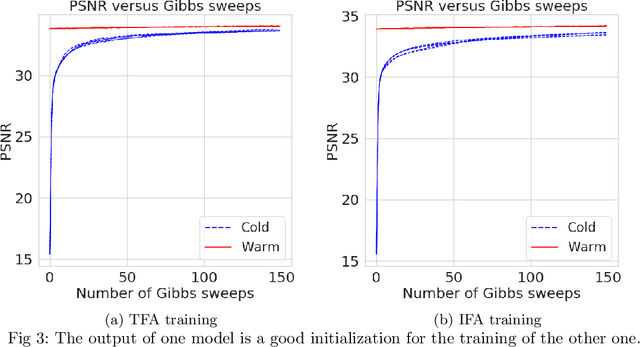
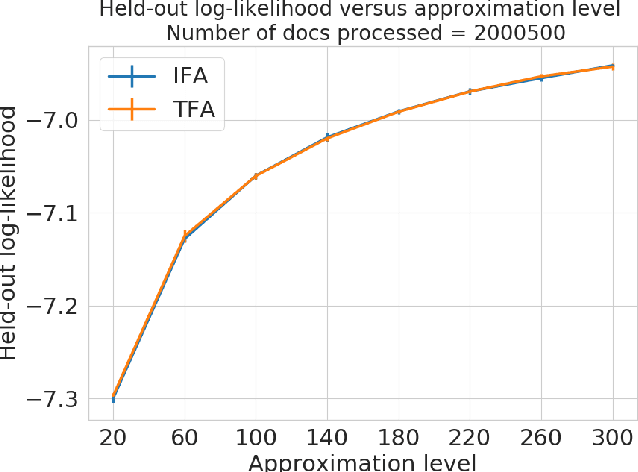
Bayesian nonparametrics based on completely random measures (CRMs) offers a flexible modeling approach when the number of clusters or latent components in a dataset is unknown. However, managing the infinite dimensionality of CRMs often leads to slow computation. Practical inference typically relies on either integrating out the infinite-dimensional parameter or using a finite approximation: a truncated finite approximation (TFA) or an independent finite approximation (IFA). The atom weights of TFAs are constructed sequentially, while the atoms of IFAs are independent, which (1) make them well-suited for parallel and distributed computation and (2) facilitates more convenient inference schemes. While IFAs have been developed in certain special cases in the past, there has not yet been a general template for construction or a systematic comparison to TFAs. We show how to construct IFAs for approximating distributions in a large family of CRMs, encompassing all those typically used in practice. We quantify the approximation error between IFAs and the target nonparametric prior, and prove that, in the worst-case, TFAs provide more component-efficient approximations than IFAs. However, in experiments on image denoising and topic modeling tasks with real data, we find that the error of Bayesian approximation methods overwhelms any finite approximation error, and IFAs perform very similarly to TFAs.