Inference on Optimal Policy Values and Other Irregular Functionals via Smoothing

Constructing confidence intervals for the value of an optimal treatment policy is an important problem in causal inference. Insight into the optimal policy value can guide the development of reward-maximizing, individualized treatment regimes. However, because the functional that defines the optimal value is non-differentiable, standard semi-parametric approaches for performing inference fail to be directly applicable. Existing approaches for handling this non-differentiability fall roughly into two camps. In one camp are estimators based on constructing smooth approximations of the optimal value. These approaches are computationally lightweight, but typically place unrealistic parametric assumptions on outcome regressions. In another camp are approaches that directly de-bias the non-smooth objective. These approaches don't place parametric assumptions on nuisance functions, but they either require the computation of intractably-many nuisance estimates, assume unrealistic $L^\infty$ nuisance convergence rates, or make strong margin assumptions that prohibit non-response to a treatment. In this paper, we revisit the problem of constructing smooth approximations of non-differentiable functionals. By carefully controlling first-order bias and second-order remainders, we show that a softmax smoothing-based estimator can be used to estimate parameters that are specified as a maximum of scores involving nuisance components. In particular, this includes the value of the optimal treatment policy as a special case. Our estimator obtains $\sqrt{n}$ convergence rates, avoids parametric restrictions/unrealistic margin assumptions, and is often statistically efficient.

Orthogonal Causal Calibration

Estimates of causal parameters such as conditional average treatment effects and conditional quantile treatment effects play an important role in real-world decision making. Given this importance, one should ensure these estimators are calibrated. While there is a rich literature on calibrating estimators of non-causal parameters, very few methods have been derived for calibrating estimators of causal parameters, or more generally estimators of quantities involving nuisance parameters. In this work, we provide a general framework for calibrating predictors involving nuisance estimation. We consider a notion of calibration defined with respect to an arbitrary, nuisance-dependent loss $\ell$, under which we say an estimator $\theta$ is calibrated if its predictions cannot be changed on any level set to decrease loss. We prove generic upper bounds on the calibration error of any causal parameter estimate $\theta$ with respect to any loss $\ell$ using a concept called Neyman Orthogonality. Our bounds involve two decoupled terms - one measuring the error in estimating the unknown nuisance parameters, and the other representing the calibration error in a hypothetical world where the learned nuisance estimates were true. We use our bound to analyze the convergence of two sample splitting algorithms for causal calibration. One algorithm, which applies to universally orthogonalizable loss functions, transforms the data into generalized pseudo-outcomes and applies an off-the-shelf calibration procedure. The other algorithm, which applies to conditionally orthogonalizable loss functions, extends the classical uniform mass binning algorithm to include nuisance estimation. Our results are exceedingly general, showing that essentially any existing calibration algorithm can be used in causal settings, with additional loss only arising from errors in nuisance estimation.

Multi-Armed Bandits with Network Interference

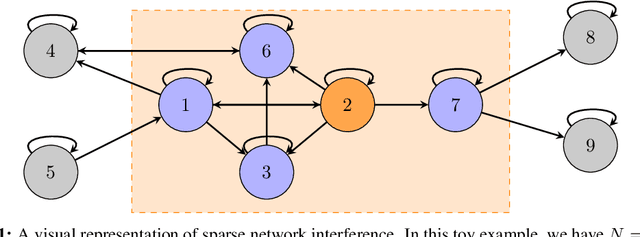
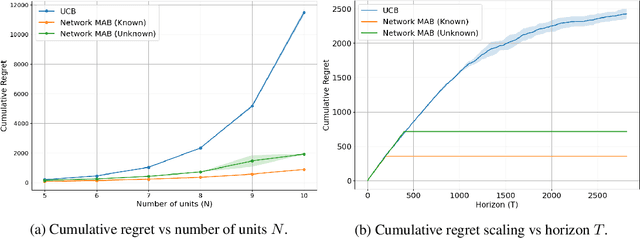
Online experimentation with interference is a common challenge in modern applications such as e-commerce and adaptive clinical trials in medicine. For example, in online marketplaces, the revenue of a good depends on discounts applied to competing goods. Statistical inference with interference is widely studied in the offline setting, but far less is known about how to adaptively assign treatments to minimize regret. We address this gap by studying a multi-armed bandit (MAB) problem where a learner (e-commerce platform) sequentially assigns one of possible $\mathcal{A}$ actions (discounts) to $N$ units (goods) over $T$ rounds to minimize regret (maximize revenue). Unlike traditional MAB problems, the reward of each unit depends on the treatments assigned to other units, i.e., there is interference across the underlying network of units. With $\mathcal{A}$ actions and $N$ units, minimizing regret is combinatorially difficult since the action space grows as $\mathcal{A}^N$. To overcome this issue, we study a sparse network interference model, where the reward of a unit is only affected by the treatments assigned to $s$ neighboring units. We use tools from discrete Fourier analysis to develop a sparse linear representation of the unit-specific reward $r_n: [\mathcal{A}]^N \rightarrow \mathbb{R} $, and propose simple, linear regression-based algorithms to minimize regret. Importantly, our algorithms achieve provably low regret both when the learner observes the interference neighborhood for all units and when it is unknown. This significantly generalizes other works on this topic which impose strict conditions on the strength of interference on a known network, and also compare regret to a markedly weaker optimal action. Empirically, we corroborate our theoretical findings via numerical simulations.

Improved Self-Normalized Concentration in Hilbert Spaces: Sublinear Regret for GP-UCB

In the kernelized bandit problem, a learner aims to sequentially compute the optimum of a function lying in a reproducing kernel Hilbert space given only noisy evaluations at sequentially chosen points. In particular, the learner aims to minimize regret, which is a measure of the suboptimality of the choices made. Arguably the most popular algorithm is the Gaussian Process Upper Confidence Bound (GP-UCB) algorithm, which involves acting based on a simple linear estimator of the unknown function. Despite its popularity, existing analyses of GP-UCB give a suboptimal regret rate, which fails to be sublinear for many commonly used kernels such as the Mat\'ern kernel. This has led to a longstanding open question: are existing regret analyses for GP-UCB tight, or can bounds be improved by using more sophisticated analytical techniques? In this work, we resolve this open question and show that GP-UCB enjoys nearly optimal regret. In particular, our results directly imply sublinear regret rates for the Mat\'ern kernel, improving over the state-of-the-art analyses and partially resolving a COLT open problem posed by Vakili et al. Our improvements rely on two key technical results. First, we use modern supermartingale techniques to construct a novel, self-normalized concentration inequality that greatly simplifies existing approaches. Second, we address the importance of regularizing in proportion to the smoothness of the underlying kernel $k$. Together, these new technical tools enable a simplified, tighter analysis of the GP-UCB algorithm.

Adaptive Principal Component Regression with Applications to Panel Data

Principal component regression (PCR) is a popular technique for fixed-design error-in-variables regression, a generalization of the linear regression setting in which the observed covariates are corrupted with random noise. We provide the first time-uniform finite sample guarantees for online (regularized) PCR whenever data is collected adaptively. Since the proof techniques for analyzing PCR in the fixed design setting do not readily extend to the online setting, our results rely on adapting tools from modern martingale concentration to the error-in-variables setting. As an application of our bounds, we provide a framework for experiment design in panel data settings when interventions are assigned adaptively. Our framework may be thought of as a generalization of the synthetic control and synthetic interventions frameworks, where data is collected via an adaptive intervention assignment policy.

Brownian Noise Reduction: Maximizing Privacy Subject to Accuracy Constraints

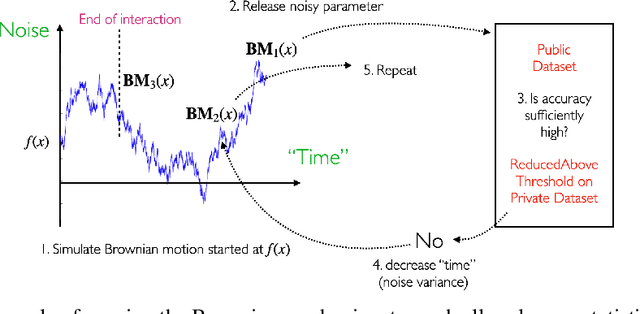
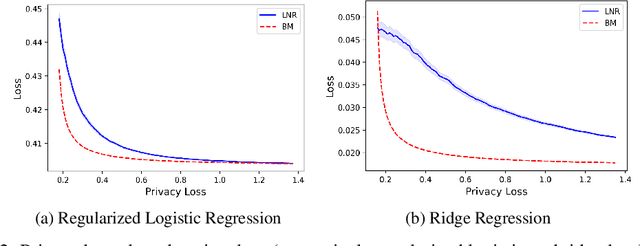
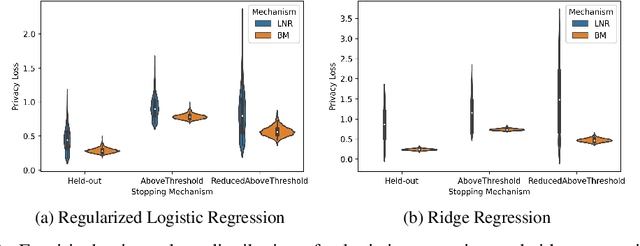
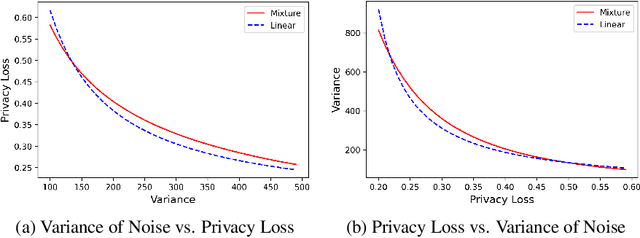
There is a disconnect between how researchers and practitioners handle privacy-utility tradeoffs. Researchers primarily operate from a privacy first perspective, setting strict privacy requirements and minimizing risk subject to these constraints. Practitioners often desire an accuracy first perspective, possibly satisfied with the greatest privacy they can get subject to obtaining sufficiently small error. Ligett et al. have introduced a "noise reduction" algorithm to address the latter perspective. The authors show that by adding correlated Laplace noise and progressively reducing it on demand, it is possible to produce a sequence of increasingly accurate estimates of a private parameter while only paying a privacy cost for the least noisy iterate released. In this work, we generalize noise reduction to the setting of Gaussian noise, introducing the Brownian mechanism. The Brownian mechanism works by first adding Gaussian noise of high variance corresponding to the final point of a simulated Brownian motion. Then, at the practitioner's discretion, noise is gradually decreased by tracing back along the Brownian path to an earlier time. Our mechanism is more naturally applicable to the common setting of bounded $\ell_2$-sensitivity, empirically outperforms existing work on common statistical tasks, and provides customizable control of privacy loss over the entire interaction with the practitioner. We complement our Brownian mechanism with ReducedAboveThreshold, a generalization of the classical AboveThreshold algorithm that provides adaptive privacy guarantees. Overall, our results demonstrate that one can meet utility constraints while still maintaining strong levels of privacy.

Fully Adaptive Composition in Differential Privacy

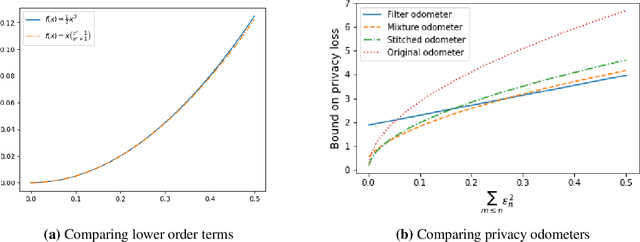
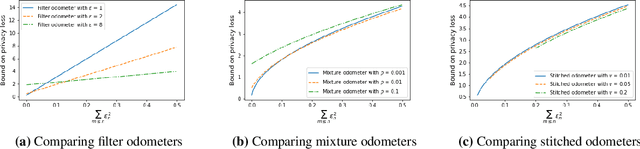
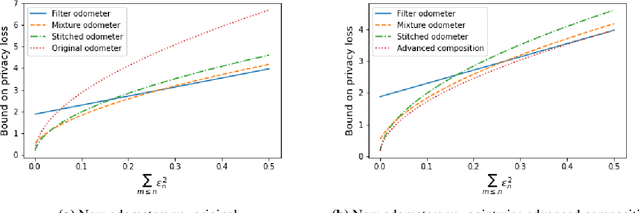
Composition is a key feature of differential privacy. Well-known advanced composition theorems allow one to query a private database quadratically more times than basic privacy composition would permit. However, these results require that the privacy parameters of all algorithms be fixed before interacting with the data. To address this, Rogers et al. introduced fully adaptive composition, wherein both algorithms and their privacy parameters can be selected adaptively. The authors introduce two probabilistic objects to measure privacy in adaptive composition: privacy filters, which provide differential privacy guarantees for composed interactions, and privacy odometers, time-uniform bounds on privacy loss. There are substantial gaps between advanced composition and existing filters and odometers. First, existing filters place stronger assumptions on the algorithms being composed. Second, these odometers and filters suffer from large constants, making them impractical. We construct filters that match the tightness of advanced composition, including constants, despite allowing for adaptively chosen privacy parameters. We also construct several general families of odometers. These odometers can match the tightness of advanced composition at an arbitrary, preselected point in time, or at all points in time simultaneously, up to a doubly-logarithmic factor. We obtain our results by leveraging recent advances in time-uniform martingale concentration. In sum, we show that fully adaptive privacy is obtainable at almost no loss, and conjecture that our results are essentially unimprovable (even in constants) in general.

Efficient Formal Safety Analysis of Neural Networks

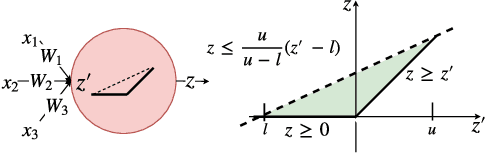
Neural networks are increasingly deployed in real-world safety-critical domains such as autonomous driving, aircraft collision avoidance, and malware detection. However, these networks have been shown to often mispredict on inputs with minor adversarial or even accidental perturbations. Consequences of such errors can be disastrous and even potentially fatal as shown by the recent Tesla autopilot crash. Thus, there is an urgent need for formal analysis systems that can rigorously check neural networks for violations of different safety properties such as robustness against adversarial perturbations within a certain $L$-norm of a given image. An effective safety analysis system for a neural network must be able to either ensure that a safety property is satisfied by the network or find a counterexample, i.e., an input for which the network will violate the property. Unfortunately, most existing techniques for performing such analysis struggle to scale beyond very small networks and the ones that can scale to larger networks suffer from high false positives and cannot produce concrete counterexamples in case of a property violation. In this paper, we present a new efficient approach for rigorously checking different safety properties of neural networks that significantly outperforms existing approaches by multiple orders of magnitude. Our approach can check different safety properties and find concrete counterexamples for networks that are 10$\times$ larger than the ones supported by existing analysis techniques. We believe that our approach to estimating tight output bounds of a network for a given input range can also help improve the explainability of neural networks and guide the training process of more robust neural networks.

Formal Security Analysis of Neural Networks using Symbolic Intervals

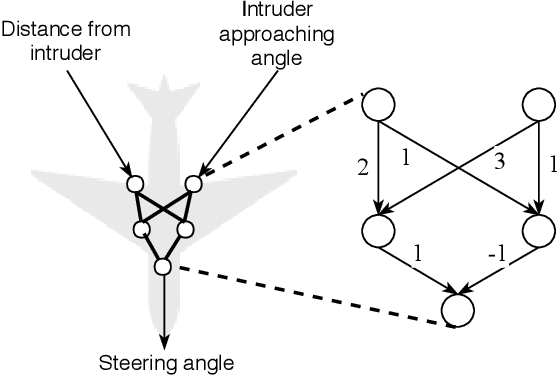
Due to the increasing deployment of Deep Neural Networks (DNNs) in real-world security-critical domains including autonomous vehicles and collision avoidance systems, formally checking security properties of DNNs, especially under different attacker capabilities, is becoming crucial. Most existing security testing techniques for DNNs try to find adversarial examples without providing any formal security guarantees about the non-existence of such adversarial examples. Recently, several projects have used different types of Satisfiability Modulo Theory (SMT) solvers to formally check security properties of DNNs. However, all of these approaches are limited by the high overhead caused by the solver. In this paper, we present a new direction for formally checking security properties of DNNs without using SMT solvers. Instead, we leverage interval arithmetic to compute rigorous bounds on the DNN outputs. Our approach, unlike existing solver-based approaches, is easily parallelizable. We further present symbolic interval analysis along with several other optimizations to minimize overestimations of output bounds. We design, implement, and evaluate our approach as part of ReluVal, a system for formally checking security properties of Relu-based DNNs. Our extensive empirical results show that ReluVal outperforms Reluplex, a state-of-the-art solver-based system, by 200 times on average. On a single 8-core machine without GPUs, within 4 hours, ReluVal is able to verify a security property that Reluplex deemed inconclusive due to timeout after running for more than 5 days. Our experiments demonstrate that symbolic interval analysis is a promising new direction towards rigorously analyzing different security properties of DNNs.