Privacy-Preserving Race/Ethnicity Estimation for Algorithmic Bias Measurement in the U.S

AI fairness measurements, including tests for equal treatment, often take the form of disaggregated evaluations of AI systems. Such measurements are an important part of Responsible AI operations. These measurements compare system performance across demographic groups or sub-populations and typically require member-level demographic signals such as gender, race, ethnicity, and location. However, sensitive member-level demographic attributes like race and ethnicity can be challenging to obtain and use due to platform choices, legal constraints, and cultural norms. In this paper, we focus on the task of enabling AI fairness measurements on race/ethnicity for \emph{U.S. LinkedIn members} in a privacy-preserving manner. We present the Privacy-Preserving Probabilistic Race/Ethnicity Estimation (PPRE) method for performing this task. PPRE combines the Bayesian Improved Surname Geocoding (BISG) model, a sparse LinkedIn survey sample of self-reported demographics, and privacy-enhancing technologies like secure two-party computation and differential privacy to enable meaningful fairness measurements while preserving member privacy. We provide details of the PPRE method and its privacy guarantees. We then illustrate sample measurement operations. We conclude with a review of open research and engineering challenges for expanding our privacy-preserving fairness measurement capabilities.

Adaptive Privacy Composition for Accuracy-first Mechanisms

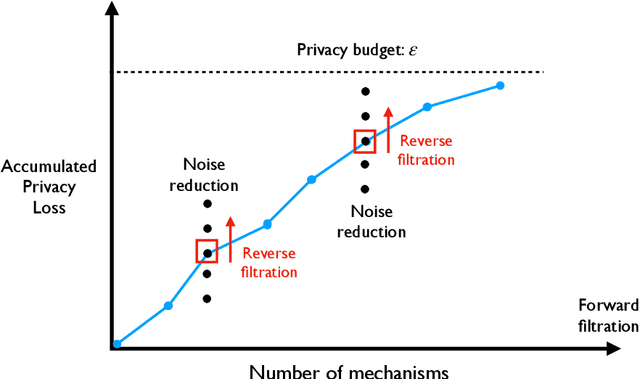
In many practical applications of differential privacy, practitioners seek to provide the best privacy guarantees subject to a target level of accuracy. A recent line of work by \cite{LigettNeRoWaWu17, WhitehouseWuRaRo22} has developed such accuracy-first mechanisms by leveraging the idea of \emph{noise reduction} that adds correlated noise to the sufficient statistic in a private computation and produces a sequence of increasingly accurate answers. A major advantage of noise reduction mechanisms is that the analysts only pay the privacy cost of the least noisy or most accurate answer released. Despite this appealing property in isolation, there has not been a systematic study on how to use them in conjunction with other differentially private mechanisms. A fundamental challenge is that the privacy guarantee for noise reduction mechanisms is (necessarily) formulated as \emph{ex-post privacy} that bounds the privacy loss as a function of the released outcome. Furthermore, there has yet to be any study on how ex-post private mechanisms compose, which allows us to track the accumulated privacy over several mechanisms. We develop privacy filters \citep{RogersRoUlVa16, FeldmanZr21, WhitehouseRaRoWu22} that allow an analyst to adaptively switch between differentially private and ex-post private mechanisms subject to an overall privacy guarantee.

Brownian Noise Reduction: Maximizing Privacy Subject to Accuracy Constraints

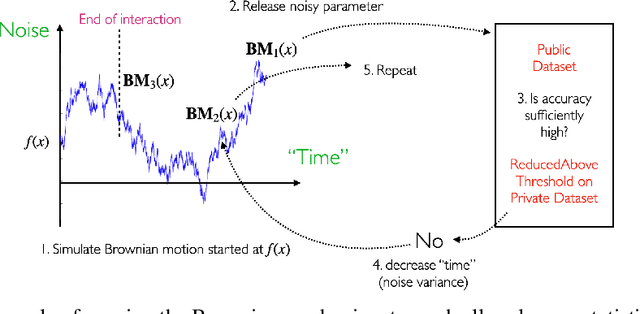
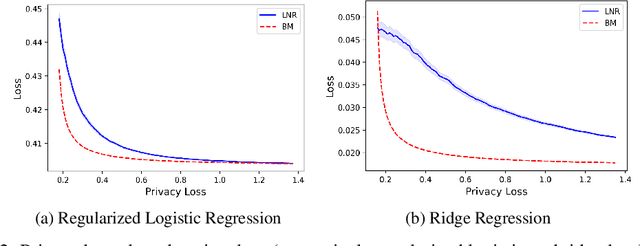
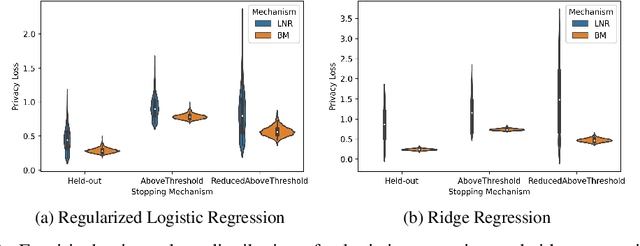
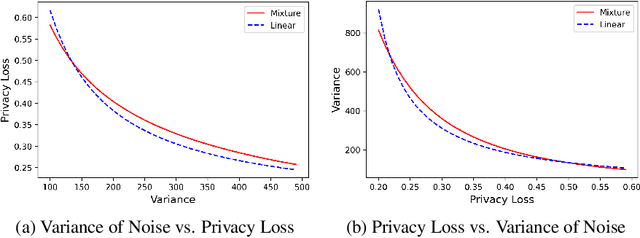
There is a disconnect between how researchers and practitioners handle privacy-utility tradeoffs. Researchers primarily operate from a privacy first perspective, setting strict privacy requirements and minimizing risk subject to these constraints. Practitioners often desire an accuracy first perspective, possibly satisfied with the greatest privacy they can get subject to obtaining sufficiently small error. Ligett et al. have introduced a "noise reduction" algorithm to address the latter perspective. The authors show that by adding correlated Laplace noise and progressively reducing it on demand, it is possible to produce a sequence of increasingly accurate estimates of a private parameter while only paying a privacy cost for the least noisy iterate released. In this work, we generalize noise reduction to the setting of Gaussian noise, introducing the Brownian mechanism. The Brownian mechanism works by first adding Gaussian noise of high variance corresponding to the final point of a simulated Brownian motion. Then, at the practitioner's discretion, noise is gradually decreased by tracing back along the Brownian path to an earlier time. Our mechanism is more naturally applicable to the common setting of bounded $\ell_2$-sensitivity, empirically outperforms existing work on common statistical tasks, and provides customizable control of privacy loss over the entire interaction with the practitioner. We complement our Brownian mechanism with ReducedAboveThreshold, a generalization of the classical AboveThreshold algorithm that provides adaptive privacy guarantees. Overall, our results demonstrate that one can meet utility constraints while still maintaining strong levels of privacy.

Fully Adaptive Composition in Differential Privacy

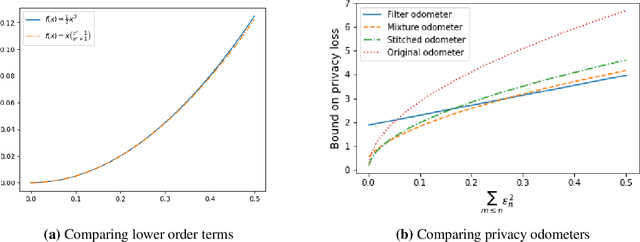
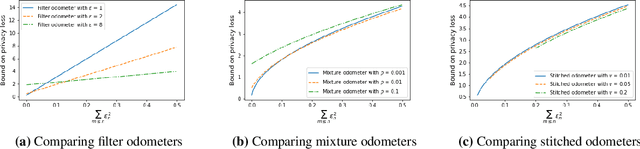
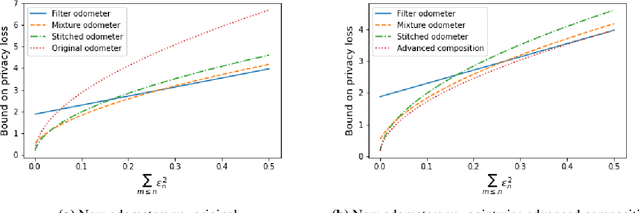
Composition is a key feature of differential privacy. Well-known advanced composition theorems allow one to query a private database quadratically more times than basic privacy composition would permit. However, these results require that the privacy parameters of all algorithms be fixed before interacting with the data. To address this, Rogers et al. introduced fully adaptive composition, wherein both algorithms and their privacy parameters can be selected adaptively. The authors introduce two probabilistic objects to measure privacy in adaptive composition: privacy filters, which provide differential privacy guarantees for composed interactions, and privacy odometers, time-uniform bounds on privacy loss. There are substantial gaps between advanced composition and existing filters and odometers. First, existing filters place stronger assumptions on the algorithms being composed. Second, these odometers and filters suffer from large constants, making them impractical. We construct filters that match the tightness of advanced composition, including constants, despite allowing for adaptively chosen privacy parameters. We also construct several general families of odometers. These odometers can match the tightness of advanced composition at an arbitrary, preselected point in time, or at all points in time simultaneously, up to a doubly-logarithmic factor. We obtain our results by leveraging recent advances in time-uniform martingale concentration. In sum, we show that fully adaptive privacy is obtainable at almost no loss, and conjecture that our results are essentially unimprovable (even in constants) in general.

Unifying Privacy Loss Composition for Data Analytics

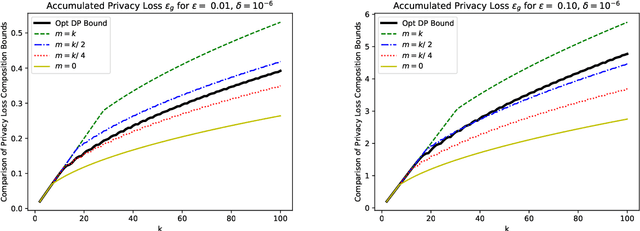
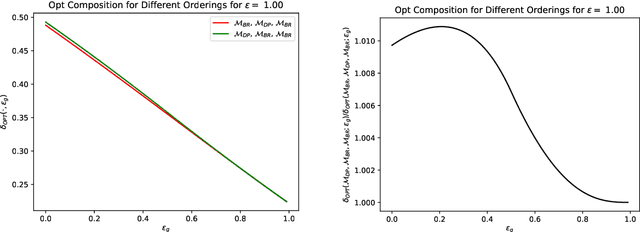
Differential privacy (DP) provides rigorous privacy guarantees on individual's data while also allowing for accurate statistics to be conducted on the overall, sensitive dataset. To design a private system, first private algorithms must be designed that can quantify the privacy loss of each outcome that is released. However, private algorithms that inject noise into the computation are not sufficient to ensure individuals' data is protected due to many noisy results ultimately concentrating to the true, non-privatized result. Hence there have been several works providing precise formulas for how the privacy loss accumulates over multiple interactions with private algorithms. However, these formulas either provide very general bounds on the privacy loss, at the cost of being overly pessimistic for certain types of private algorithms, or they can be too narrow in scope to apply to general privacy systems. In this work, we unify existing privacy loss composition bounds for special classes of differentially private (DP) algorithms along with general DP composition bounds. In particular, we provide strong privacy loss bounds when an analyst may select pure DP, bounded range (e.g. exponential mechanisms), or concentrated DP mechanisms in any order. We also provide optimal privacy loss bounds that apply when an analyst can select pure DP and bounded range mechanisms in a batch, i.e. non-adaptively. Further, when an analyst selects mechanisms within each class adaptively, we show a difference in privacy loss between different, predetermined orderings of pure DP and bounded range mechanisms. Lastly, we compare the composition bounds of Laplace and Gaussian mechanisms based on histogram datasets.

Guaranteed Validity for Empirical Approaches to Adaptive Data Analysis

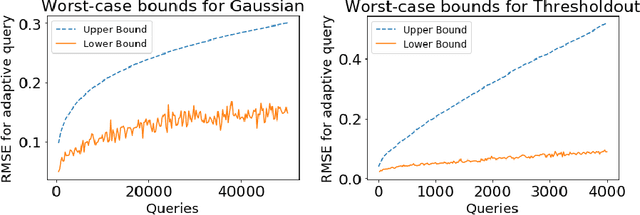
We design a general framework for answering adaptive statistical queries that focuses on providing explicit confidence intervals along with point estimates. Prior work in this area has either focused on providing tight confidence intervals for specific analyses, or providing general worst-case bounds for point estimates. Unfortunately, as we observe, these worst-case bounds are loose in many settings --- often not even beating simple baselines like sample splitting. Our main contribution is to design a framework for providing valid, instance-specific confidence intervals for point estimates that can be generated by heuristics. When paired with good heuristics, this method gives guarantees that are orders of magnitude better than the best worst-case bounds. We provide a Python library implementing our method.

Protection Against Reconstruction and Its Applications in Private Federated Learning

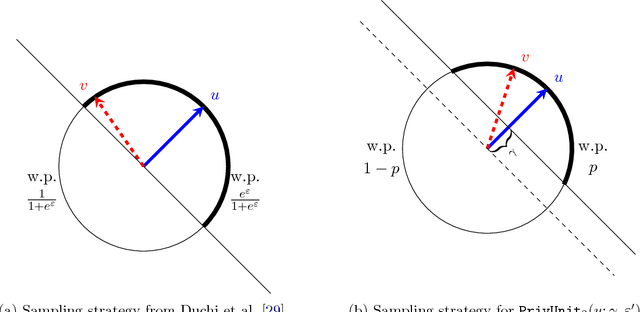
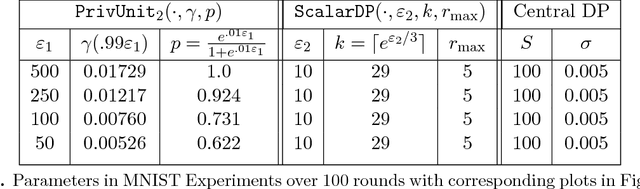
Federated learning has become an exciting direction for both research and practical training of models with user data. Although data remains decentralized in federated learning, it is common to assume that the model updates are sent in the clear from the devices to the server. Differential privacy has been proposed as a way to ensure the model remains private, but this does not address the issue that model updates can be seen on the server, and lead to leakage of user data. Local differential privacy is one of the strongest forms of privacy protection so that each individual's data is privatized. However, local differential privacy, as it is traditionally used, may prove to be too stringent of a privacy condition in many high dimensional problems, such as in distributed model fitting. We propose a new paradigm for local differential privacy by providing protections against certain adversaries. Specifically, we ensure that adversaries with limited prior information cannot reconstruct, with high probability, the original data within some prescribed tolerance. This interpretation allows us to consider larger privacy parameters. We then design (optimal) DP mechanisms in this large privacy parameter regime. In this work, we combine local privacy protections along with central differential privacy to present a practical approach to do model training privately. Further, we show that these privacy restrictions maintain utility in image classification and language models that is comparable to federated learning without these privacy restrictions.

Learning from Rational Behavior: Predicting Solutions to Unknown Linear Programs

We define and study the problem of predicting the solution to a linear program (LP) given only partial information about its objective and constraints. This generalizes the problem of learning to predict the purchasing behavior of a rational agent who has an unknown objective function, that has been studied under the name "Learning from Revealed Preferences". We give mistake bound learning algorithms in two settings: in the first, the objective of the LP is known to the learner but there is an arbitrary, fixed set of constraints which are unknown. Each example is defined by an additional known constraint and the goal of the learner is to predict the optimal solution of the LP given the union of the known and unknown constraints. This models the problem of predicting the behavior of a rational agent whose goals are known, but whose resources are unknown. In the second setting, the objective of the LP is unknown, and changing in a controlled way. The constraints of the LP may also change every day, but are known. An example is given by a set of constraints and partial information about the objective, and the task of the learner is again to predict the optimal solution of the partially known LP.

Max-Information, Differential Privacy, and Post-Selection Hypothesis Testing

In this paper, we initiate a principled study of how the generalization properties of approximate differential privacy can be used to perform adaptive hypothesis testing, while giving statistically valid $p$-value corrections. We do this by observing that the guarantees of algorithms with bounded approximate max-information are sufficient to correct the $p$-values of adaptively chosen hypotheses, and then by proving that algorithms that satisfy $(\epsilon,\delta)$-differential privacy have bounded approximate max information when their inputs are drawn from a product distribution. This substantially extends the known connection between differential privacy and max-information, which previously was only known to hold for (pure) $(\epsilon,0)$-differential privacy. It also extends our understanding of max-information as a partially unifying measure controlling the generalization properties of adaptive data analyses. We also show a lower bound, proving that (despite the strong composition properties of max-information), when data is drawn from a product distribution, $(\epsilon,\delta)$-differentially private algorithms can come first in a composition with other algorithms satisfying max-information bounds, but not necessarily second if the composition is required to itself satisfy a nontrivial max-information bound. This, in particular, implies that the connection between $(\epsilon,\delta)$-differential privacy and max-information holds only for inputs drawn from product distributions, unlike the connection between $(\epsilon,0)$-differential privacy and max-information.

Do Prices Coordinate Markets?

Walrasian equilibrium prices can be said to coordinate markets: They support a welfare optimal allocation in which each buyer is buying bundle of goods that is individually most preferred. However, this clean story has two caveats. First, the prices alone are not sufficient to coordinate the market, and buyers may need to select among their most preferred bundles in a coordinated way to find a feasible allocation. Second, we don't in practice expect to encounter exact equilibrium prices tailored to the market, but instead only approximate prices, somehow encoding "distributional" information about the market. How well do prices work to coordinate markets when tie-breaking is not coordinated, and they encode only distributional information? We answer this question. First, we provide a genericity condition such that for buyers with Matroid Based Valuations, overdemand with respect to equilibrium prices is at most 1, independent of the supply of goods, even when tie-breaking is done in an uncoordinated fashion. Second, we provide learning-theoretic results that show that such prices are robust to changing the buyers in the market, so long as all buyers are sampled from the same (unknown) distribution.