Learning Differentially Private Mechanisms

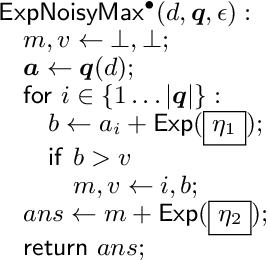
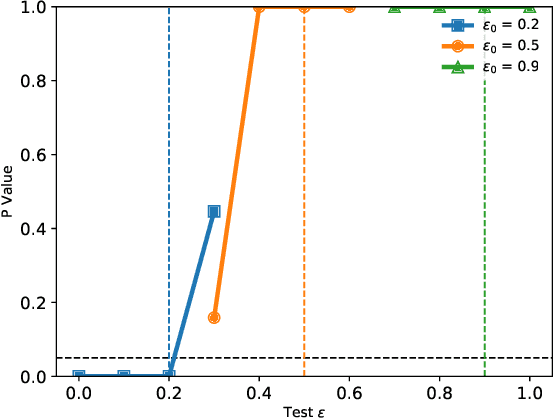
Differential privacy is a formal, mathematical definition of data privacy that has gained traction in academia, industry, and government. The task of correctly constructing differentially private algorithms is non-trivial, and mistakes have been made in foundational algorithms. Currently, there is no automated support for converting an existing, non-private program into a differentially private version. In this paper, we propose a technique for automatically learning an accurate and differentially private version of a given non-private program. We show how to solve this difficult program synthesis problem via a combination of techniques: carefully picking representative example inputs, reducing the problem to continuous optimization, and mapping the results back to symbolic expressions. We demonstrate that our approach is able to learn foundational algorithms from the differential privacy literature and significantly outperforms natural program synthesis baselines.

Analyzing Accuracy Loss in Randomized Smoothing Defenses

Recent advances in machine learning (ML) algorithms, especially deep neural networks (DNNs), have demonstrated remarkable success (sometimes exceeding human-level performance) on several tasks, including face and speech recognition. However, ML algorithms are vulnerable to \emph{adversarial attacks}, such test-time, training-time, and backdoor attacks. In test-time attacks an adversary crafts adversarial examples, which are specially crafted perturbations imperceptible to humans which, when added to an input example, force a machine learning model to misclassify the given input example. Adversarial examples are a concern when deploying ML algorithms in critical contexts, such as information security and autonomous driving. Researchers have responded with a plethora of defenses. One promising defense is \emph{randomized smoothing} in which a classifier's prediction is smoothed by adding random noise to the input example we wish to classify. In this paper, we theoretically and empirically explore randomized smoothing. We investigate the effect of randomized smoothing on the feasible hypotheses space, and show that for some noise levels the set of hypotheses which are feasible shrinks due to smoothing, giving one reason why the natural accuracy drops after smoothing. To perform our analysis, we introduce a model for randomized smoothing which abstracts away specifics, such as the exact distribution of the noise. We complement our theoretical results with extensive experiments.

Advances and Open Problems in Federated Learning

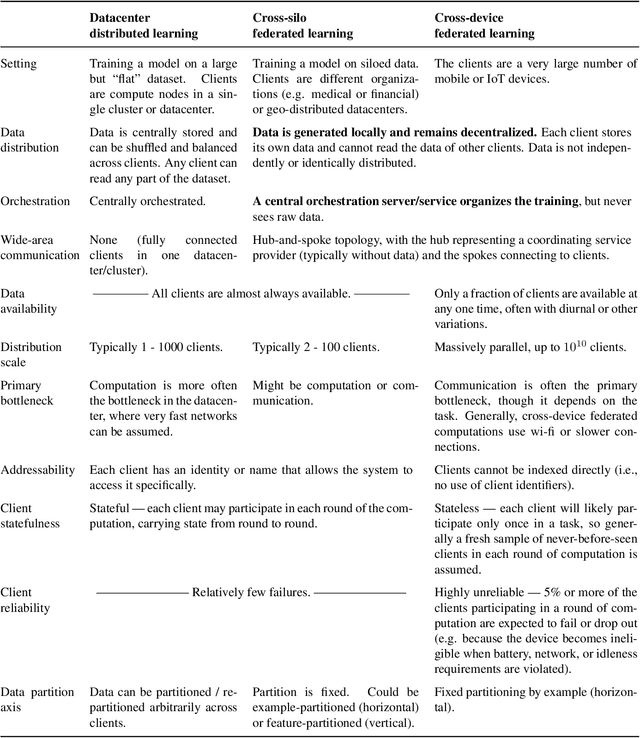
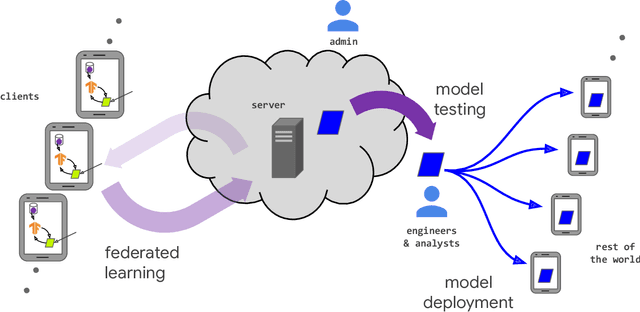
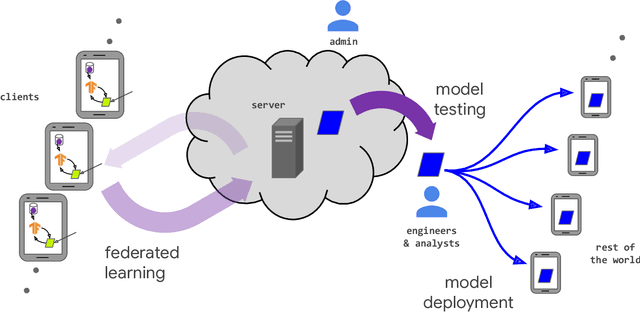
Federated learning (FL) is a machine learning setting where many clients (e.g. mobile devices or whole organizations) collaboratively train a model under the orchestration of a central server (e.g. service provider), while keeping the training data decentralized. FL embodies the principles of focused data collection and minimization, and can mitigate many of the systemic privacy risks and costs resulting from traditional, centralized machine learning and data science approaches. Motivated by the explosive growth in FL research, this paper discusses recent advances and presents an extensive collection of open problems and challenges.

Hypothesis Testing Interpretations and Renyi Differential Privacy

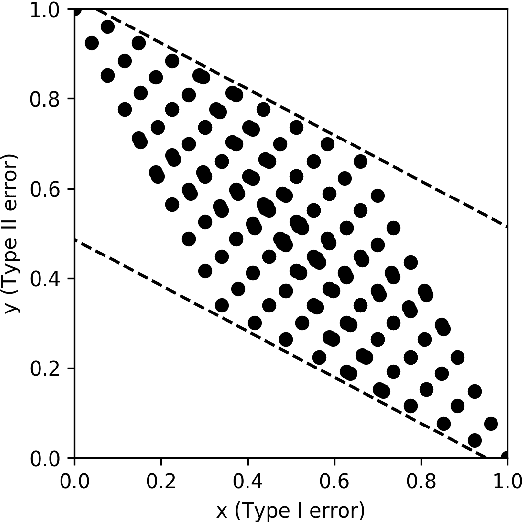
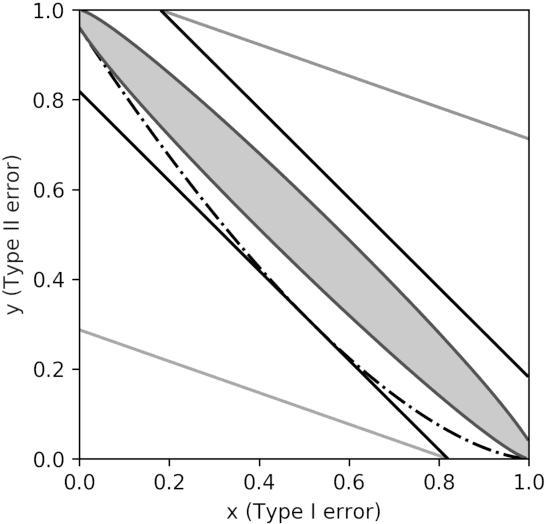
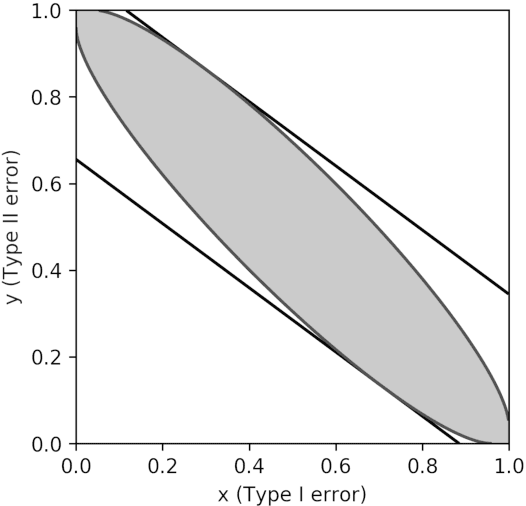
Differential privacy is the gold standard in data privacy, with applications in the public and private sectors. While differential privacy is a formal mathematical definition from the theoretical computer science literature, it is also understood by statisticians and data experts thanks to its hypothesis testing interpretation. This informally says that one cannot effectively test whether a specific individual has contributed her data by observing the output of a private mechanism---any test cannot have both high significance and high power. In this paper, we show that recently proposed relaxations of differential privacy based on R\'enyi divergence do not enjoy a similar interpretation. Specifically, we introduce the notion of $k$-generatedness for an arbitrary divergence, where the parameter $k$ captures the hypothesis testing complexity of the divergence. We show that the divergence used for differential privacy is 2-generated, and hence it satisfies the hypothesis testing interpretation. In contrast, R\'enyi divergence is only $\infty$-generated, and hence has no hypothesis testing interpretation. We also show sufficient conditions for general divergences to be $k$-generated.

Data Poisoning against Differentially-Private Learners: Attacks and Defenses

Data poisoning attacks aim to manipulate the model produced by a learning algorithm by adversarially modifying the training set. We consider differential privacy as a defensive measure against this type of attack. We show that such learners are resistant to data poisoning attacks when the adversary is only able to poison a small number of items. However, this protection degrades as the adversary poisons more data. To illustrate, we design attack algorithms targeting objective and output perturbation learners, two standard approaches to differentially-private machine learning. Experiments show that our methods are effective when the attacker is allowed to poison sufficiently many training items.

Do Prices Coordinate Markets?

Walrasian equilibrium prices can be said to coordinate markets: They support a welfare optimal allocation in which each buyer is buying bundle of goods that is individually most preferred. However, this clean story has two caveats. First, the prices alone are not sufficient to coordinate the market, and buyers may need to select among their most preferred bundles in a coordinated way to find a feasible allocation. Second, we don't in practice expect to encounter exact equilibrium prices tailored to the market, but instead only approximate prices, somehow encoding "distributional" information about the market. How well do prices work to coordinate markets when tie-breaking is not coordinated, and they encode only distributional information? We answer this question. First, we provide a genericity condition such that for buyers with Matroid Based Valuations, overdemand with respect to equilibrium prices is at most 1, independent of the supply of goods, even when tie-breaking is done in an uncoordinated fashion. Second, we provide learning-theoretic results that show that such prices are robust to changing the buyers in the market, so long as all buyers are sampled from the same (unknown) distribution.

Dual Query: Practical Private Query Release for High Dimensional Data

We present a practical, differentially private algorithm for answering a large number of queries on high dimensional datasets. Like all algorithms for this task, ours necessarily has worst-case complexity exponential in the dimension of the data. However, our algorithm packages the computationally hard step into a concisely defined integer program, which can be solved non-privately using standard solvers. We prove accuracy and privacy theorems for our algorithm, and then demonstrate experimentally that our algorithm performs well in practice. For example, our algorithm can efficiently and accurately answer millions of queries on the Netflix dataset, which has over 17,000 attributes; this is an improvement on the state of the art by multiple orders of magnitude.

Privately Solving Linear Programs

In this paper, we initiate the systematic study of solving linear programs under differential privacy. The first step is simply to define the problem: to this end, we introduce several natural classes of private linear programs that capture different ways sensitive data can be incorporated into a linear program. For each class of linear programs we give an efficient, differentially private solver based on the multiplicative weights framework, or we give an impossibility result.