Gilles Barthe
Scaling Guarantees for Nearest Counterfactual Explanations
Oct 10, 2020
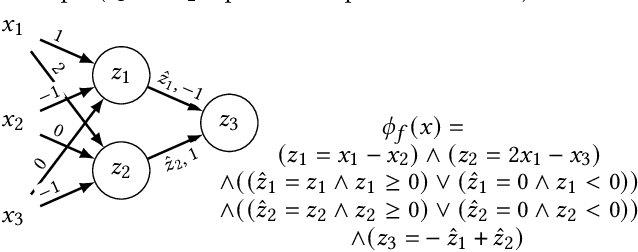
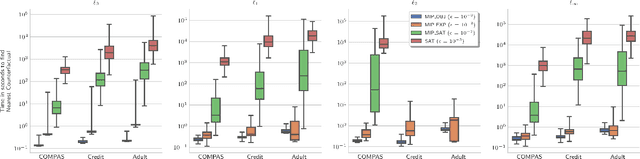
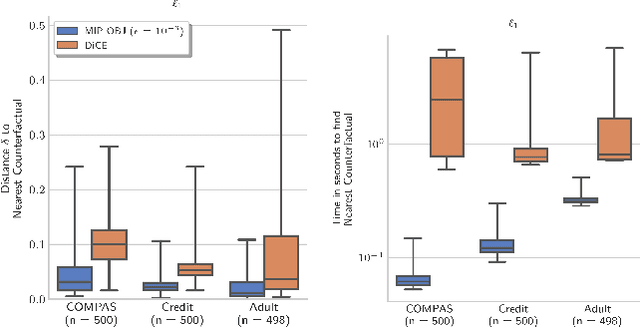
Abstract:Counterfactual explanations (CFE) are being widely used to explain algorithmic decisions, especially in consequential decision-making contexts (e.g., loan approval or pretrial bail). In this context, CFEs aim to provide individuals affected by an algorithmic decision with the most similar individual (i.e., nearest individual) with a different outcome. However, while an increasing number of works propose algorithms to compute CFEs, such approaches either lack in optimality of distance (i.e., they do not return the nearest individual) and perfect coverage (i.e., they do not provide a CFE for all individuals); or they cannot handle complex models, such as neural networks. In this work, we provide a framework based on Mixed-Integer Programming (MIP) to compute nearest counterfactual explanations with provable guarantees and with runtimes comparable to gradient-based approaches. Our experiments on the Adult, COMPAS, and Credit datasets show that, in contrast with previous methods, our approach allows for efficiently computing diverse CFEs with both distance guarantees and perfect coverage.
A survey of algorithmic recourse: definitions, formulations, solutions, and prospects
Oct 08, 2020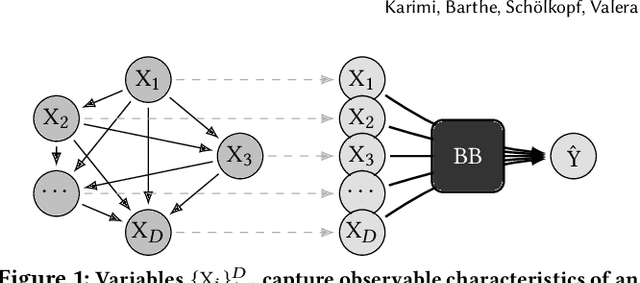
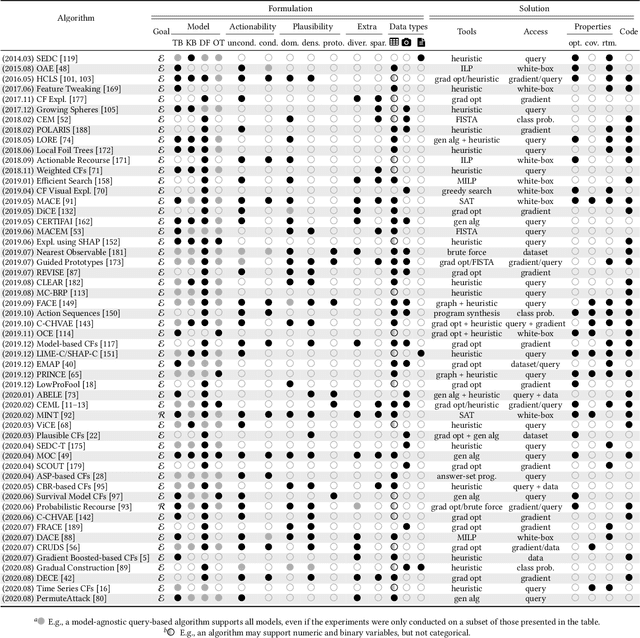
Abstract:Machine learning is increasingly used to inform decision-making in sensitive situations where decisions have consequential effects on individuals' lives. In these settings, in addition to requiring models to be accurate and robust, socially relevant values such as fairness, privacy, accountability, and explainability play an important role for the adoption and impact of said technologies. In this work, we focus on algorithmic recourse, which is concerned with providing explanations and recommendations to individuals who are unfavourably treated by automated decision-making systems. We first perform an extensive literature review, and align the efforts of many authors by presenting unified definitions, formulations, and solutions to recourse. Then, we provide an overview of the prospective research directions towards which the community may engage, challenging existing assumptions and making explicit connections to other ethical challenges such as security, privacy, and fairness.
Privacy Amplification by Mixing and Diffusion Mechanisms
May 29, 2019
Abstract:A fundamental result in differential privacy states that the privacy guarantees of a mechanism are preserved by any post-processing of its output. In this paper we investigate under what conditions stochastic post-processing can amplify the privacy of a mechanism. By interpreting post-processing as the application of a Markov operator, we first give a series of amplification results in terms of uniform mixing properties of the Markov process defined by said operator. Next we provide amplification bounds in terms of coupling arguments which can be applied in cases where uniform mixing is not available. Finally, we introduce a new family of mechanisms based on diffusion processes which are closed under post-processing, and analyze their privacy via a novel heat flow argument. As applications, we show that the rate of "privacy amplification by iteration" in Noisy SGD introduced by Feldman et al. [FOCS'18] admits an exponential improvement in the strongly convex case, and propose a simple mechanism based on the Ornstein-Uhlenbeck process which has better mean squared error than the Gaussian mechanism when releasing a bounded function of the data.
Model-Agnostic Counterfactual Explanations for Consequential Decisions
May 28, 2019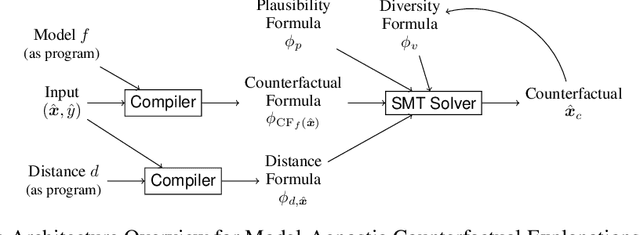



Abstract:Predictive models are being increasingly used to support consequential decision making at the individual level in contexts such as pretrial bail and loan approval. As a result, there is increasing social and legal pressure to provide explanations that help the affected individuals not only to understand why a prediction was output, but also how to act to obtain a desired outcome. To this end, several works have proposed methods to generate counterfactual explanations. However, they are often restricted to a particular subset of models (e.g., decision trees or linear models), and cannot directly handle the mixed (numerical and nominal) nature of the features describing each individual. In this paper, we propose a model-agnostic algorithm to generate counterfactual explanations that builds on the standard theory and tools from formal verification. Specifically, our algorithm solves a sequence of satisfiability problems, where a wide variety of predictive models and distances in mixed feature spaces, as well as natural notions of plausibility and diversity, are represented as logic formulas. Our experiments on real-world data demonstrate that our approach can flexibly handle widely deployed predictive models, while providing meaningfully closer counterfactuals than existing approaches.
Hypothesis Testing Interpretations and Renyi Differential Privacy
May 24, 2019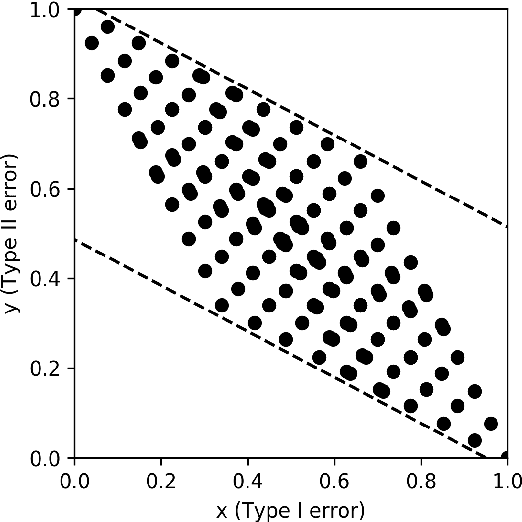
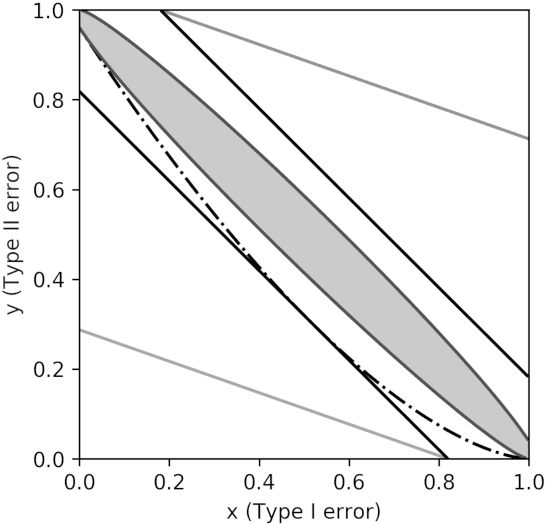
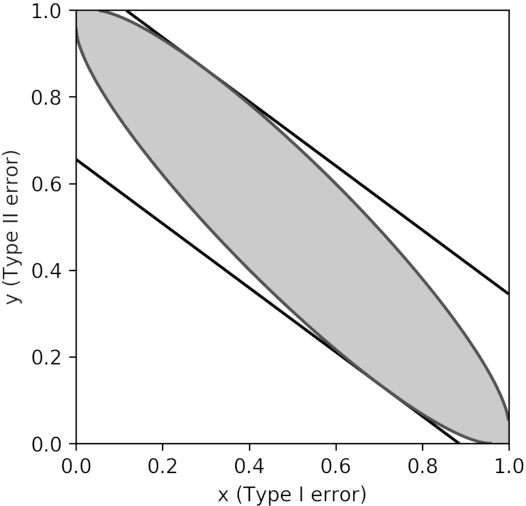
Abstract:Differential privacy is the gold standard in data privacy, with applications in the public and private sectors. While differential privacy is a formal mathematical definition from the theoretical computer science literature, it is also understood by statisticians and data experts thanks to its hypothesis testing interpretation. This informally says that one cannot effectively test whether a specific individual has contributed her data by observing the output of a private mechanism---any test cannot have both high significance and high power. In this paper, we show that recently proposed relaxations of differential privacy based on R\'enyi divergence do not enjoy a similar interpretation. Specifically, we introduce the notion of $k$-generatedness for an arbitrary divergence, where the parameter $k$ captures the hypothesis testing complexity of the divergence. We show that the divergence used for differential privacy is 2-generated, and hence it satisfies the hypothesis testing interpretation. In contrast, R\'enyi divergence is only $\infty$-generated, and hence has no hypothesis testing interpretation. We also show sufficient conditions for general divergences to be $k$-generated.
Privacy Amplification by Subsampling: Tight Analyses via Couplings and Divergences
Jul 04, 2018
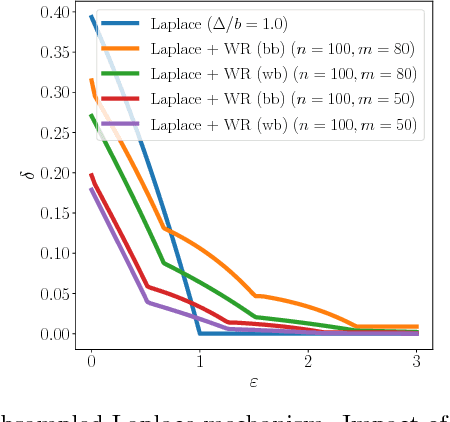
Abstract:Differential privacy comes equipped with multiple analytical tools for the design of private data analyses. One important tool is the so called "privacy amplification by subsampling" principle, which ensures that a differentially private mechanism run on a random subsample of a population provides higher privacy guarantees than when run on the entire population. Several instances of this principle have been studied for different random subsampling methods, each with an ad-hoc analysis. In this paper we present a general method that recovers and improves prior analyses, yields lower bounds and derives new instances of privacy amplification by subsampling. Our method leverages a characterization of differential privacy as a divergence which emerged in the program verification community. Furthermore, it introduces new tools, including advanced joint convexity and privacy profiles, which might be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge