Privacy Amplification by Subsampling: Tight Analyses via Couplings and Divergences

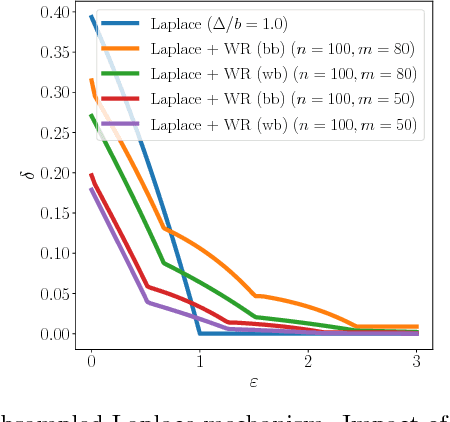
Differential privacy comes equipped with multiple analytical tools for the design of private data analyses. One important tool is the so called "privacy amplification by subsampling" principle, which ensures that a differentially private mechanism run on a random subsample of a population provides higher privacy guarantees than when run on the entire population. Several instances of this principle have been studied for different random subsampling methods, each with an ad-hoc analysis. In this paper we present a general method that recovers and improves prior analyses, yields lower bounds and derives new instances of privacy amplification by subsampling. Our method leverages a characterization of differential privacy as a divergence which emerged in the program verification community. Furthermore, it introduces new tools, including advanced joint convexity and privacy profiles, which might be of independent interest.