Tetsuya Sato
Formalizing Statistical Causality via Modal Logic
Nov 01, 2022Abstract:We propose a formal language for describing and explaining statistical causality. Concretely, we define Statistical Causality Language (StaCL) for specifying causal effects on random variables. StaCL incorporates modal operators for interventions to express causal properties between probability distributions in different possible worlds in a Kripke model. We formalize axioms for probability distributions, interventions, and causal predicates using StaCL formulas. These axioms are expressive enough to derive the rules of Pearl's do-calculus. Finally, we demonstrate by examples that StaCL can be used to prove and explain the correctness of statistical causal inference.
Sound and Relatively Complete Belief Hoare Logic for Statistical Hypothesis Testing Programs
Aug 15, 2022
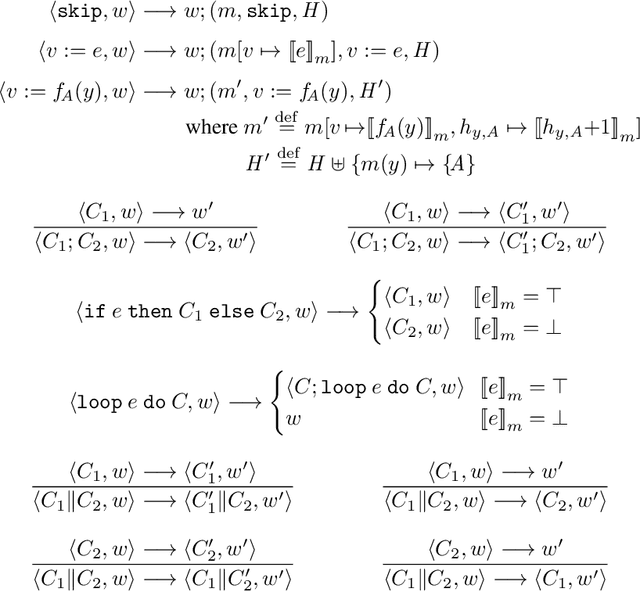


Abstract:We propose a new approach to formally describing the requirement for statistical inference and checking whether a program uses the statistical method appropriately. Specifically, we define belief Hoare logic (BHL) for formalizing and reasoning about the statistical beliefs acquired via hypothesis testing. This program logic is sound and relatively complete with respect to a Kripke model for hypothesis tests. We demonstrate by examples that BHL is useful for reasoning about practical issues in hypothesis testing. In our framework, we clarify the importance of prior beliefs in acquiring statistical beliefs through hypothesis testing, and discuss the whole picture of the justification of statistical inference inside and outside the program logic.
Hypothesis Testing Interpretations and Renyi Differential Privacy
May 24, 2019Abstract:Differential privacy is the gold standard in data privacy, with applications in the public and private sectors. While differential privacy is a formal mathematical definition from the theoretical computer science literature, it is also understood by statisticians and data experts thanks to its hypothesis testing interpretation. This informally says that one cannot effectively test whether a specific individual has contributed her data by observing the output of a private mechanism---any test cannot have both high significance and high power. In this paper, we show that recently proposed relaxations of differential privacy based on R\'enyi divergence do not enjoy a similar interpretation. Specifically, we introduce the notion of $k$-generatedness for an arbitrary divergence, where the parameter $k$ captures the hypothesis testing complexity of the divergence. We show that the divergence used for differential privacy is 2-generated, and hence it satisfies the hypothesis testing interpretation. In contrast, R\'enyi divergence is only $\infty$-generated, and hence has no hypothesis testing interpretation. We also show sufficient conditions for general divergences to be $k$-generated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge