Model-Agnostic Counterfactual Explanations for Consequential Decisions

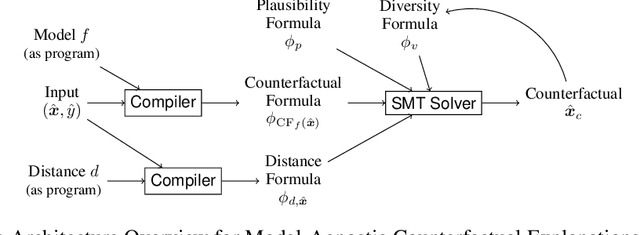
Predictive models are being increasingly used to support consequential decision making at the individual level in contexts such as pretrial bail and loan approval. As a result, there is increasing social and legal pressure to provide explanations that help the affected individuals not only to understand why a prediction was output, but also how to act to obtain a desired outcome. To this end, several works have proposed methods to generate counterfactual explanations. However, they are often restricted to a particular subset of models (e.g., decision trees or linear models), and cannot directly handle the mixed (numerical and nominal) nature of the features describing each individual. In this paper, we propose a model-agnostic algorithm to generate counterfactual explanations that builds on the standard theory and tools from formal verification. Specifically, our algorithm solves a sequence of satisfiability problems, where a wide variety of predictive models and distances in mixed feature spaces, as well as natural notions of plausibility and diversity, are represented as logic formulas. Our experiments on real-world data demonstrate that our approach can flexibly handle widely deployed predictive models, while providing meaningfully closer counterfactuals than existing approaches.