Inductive Generalization in Reinforcement Learning from Specifications

We present a novel inductive generalization framework for RL from logical specifications. Many interesting tasks in RL environments have a natural inductive structure. These inductive tasks have similar overarching goals but they differ inductively in low-level predicates and distributions. We present a generalization procedure that leverages this inductive relationship to learn a higher-order function, a policy generator, that generates appropriately adapted policies for instances of an inductive task in a zero-shot manner. An evaluation of the proposed approach on a set of challenging control benchmarks demonstrates the promise of our framework in generalizing to unseen policies for long-horizon tasks.

Finding Inductive Loop Invariants using Large Language Models

Loop invariants are fundamental to reasoning about programs with loops. They establish properties about a given loop's behavior. When they additionally are inductive, they become useful for the task of formal verification that seeks to establish strong mathematical guarantees about program's runtime behavior. The inductiveness ensures that the invariants can be checked locally without consulting the entire program, thus are indispensable artifacts in a formal proof of correctness. Finding inductive loop invariants is an undecidable problem, and despite a long history of research towards practical solutions, it remains far from a solved problem. This paper investigates the capabilities of the Large Language Models (LLMs) in offering a new solution towards this old, yet important problem. To that end, we first curate a dataset of verification problems on programs with loops. Next, we design a prompt for exploiting LLMs, obtaining inductive loop invariants, that are checked for correctness using sound symbolic tools. Finally, we explore the effectiveness of using an efficient combination of a symbolic tool and an LLM on our dataset and compare it against a purely symbolic baseline. Our results demonstrate that LLMs can help improve the state-of-the-art in automated program verification.

Synthesis with Explicit Dependencies

Quantified Boolean Formulas (QBF) extend propositional logic with quantification $\forall, \exists$. In QBF, an existentially quantified variable is allowed to depend on all universally quantified variables in its scope. Dependency Quantified Boolean Formulas (DQBF) restrict the dependencies of existentially quantified variables. In DQBF, existentially quantified variables have explicit dependencies on a subset of universally quantified variables called Henkin dependencies. Given a Boolean specification between the set of inputs and outputs, the problem of Henkin synthesis is to synthesize each output variable as a function of its Henkin dependencies such that the specification is met. Henkin synthesis has wide-ranging applications, including verification of partial circuits, controller synthesis, and circuit realizability. This work proposes a data-driven approach for Henkin synthesis called Manthan3. On an extensive evaluation of over 563 instances arising from past DQBF solving competitions, we demonstrate that Manthan3 is competitive with state-of-the-art tools. Furthermore, Manthan3 could synthesize Henkin functions for 26 benchmarks for which none of the state-of-the-art techniques could synthesize.

Engineering an Efficient Boolean Functional Synthesis Engine

Given a Boolean specification between a set of inputs and outputs, the problem of Boolean functional synthesis is to synthesise each output as a function of inputs such that the specification is met. Although the past few years have witnessed intense algorithmic development, accomplishing scalability remains the holy grail. The state-of-the-art approach combines machine learning and automated reasoning to efficiently synthesise Boolean functions. In this paper, we propose four algorithmic improvements for a data-driven framework for functional synthesis: using a dependency-driven multi-classifier to learn candidate function, extracting uniquely defined functions by interpolation, variables retention, and using lexicographic MaxSAT to repair candidates. We implement these improvements in the state-of-the-art framework, called Manthan. The proposed framework is called Manthan2. Manthan2 shows significantly improved runtime performance compared to Manthan. In an extensive experimental evaluation on 609 benchmarks, Manthan2 is able to synthesise a Boolean function vector for 509 instances compared to 356 instances solved by Manthan--- an increment of 153 instances over the state-of-the-art. To put this into perspective, Manthan improved on the prior state-of-the-art by only 76 instances.

Program Synthesis as Dependency Quantified Formula Modulo Theory

Given a specification $\varphi(X,Y)$ over inputs $X$ and output $Y$, defined over a background theory $\mathbb{T}$, the problem of program synthesis is to design a program $f$ such that $Y=f(X)$ satisfies the specification $\varphi$. Over the past decade, syntax-guided synthesis (SyGuS) has emerged as a dominant approach for program synthesis where in addition to the specification $\varphi$, the end-user also specifies a grammar $L$ to aid the underlying synthesis engine. This paper investigates the feasibility of synthesis techniques without grammar, a sub-class defined as $\mathbb{T}$-constrained synthesis. We show that $\mathbb{T}$-constrained synthesis can be reduced to DQF($\mathbb{T}$), i.e., to the problem of finding a witness of a Dependency Quantified Formula Modulo Theory. When the underlying theory is the theory of bitvectors, the corresponding DQF(BV) problem can be further reduced to Dependency Quantified Boolean Formulas (DQBF). We rely on the progress in DQBF solving to design DQBF-based synthesizers that outperform the domain-specific program synthesis techniques, thereby positioning DQBF as a core representation language for program synthesis. Our empirical analysis shows that $\mathbb{T}$-constrained synthesis can achieve significantly better performance than syntax-guided approaches. Furthermore, the general-purpose DQBF solvers perform on par with domain-specific synthesis techniques.

Learning Differentially Private Mechanisms

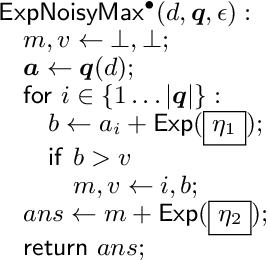
Differential privacy is a formal, mathematical definition of data privacy that has gained traction in academia, industry, and government. The task of correctly constructing differentially private algorithms is non-trivial, and mistakes have been made in foundational algorithms. Currently, there is no automated support for converting an existing, non-private program into a differentially private version. In this paper, we propose a technique for automatically learning an accurate and differentially private version of a given non-private program. We show how to solve this difficult program synthesis problem via a combination of techniques: carefully picking representative example inputs, reducing the problem to continuous optimization, and mapping the results back to symbolic expressions. We demonstrate that our approach is able to learn foundational algorithms from the differential privacy literature and significantly outperforms natural program synthesis baselines.

Phase Transition Behavior in Knowledge Compilation

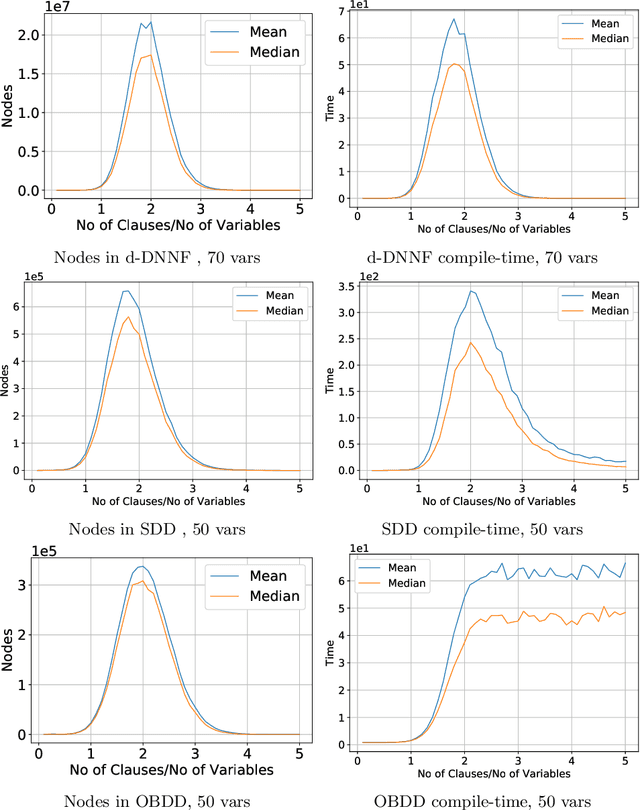
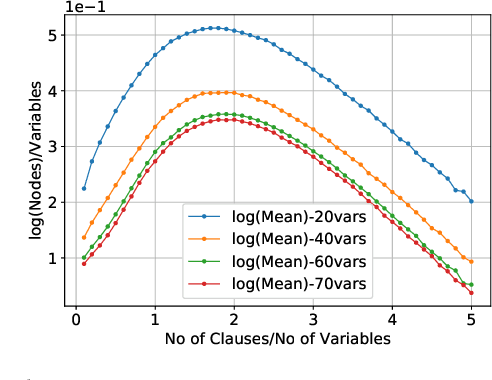
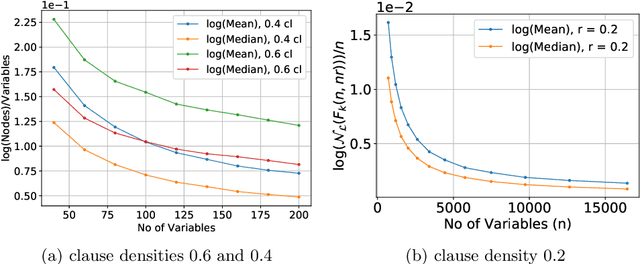
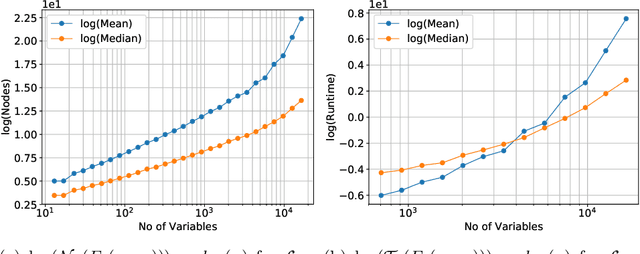
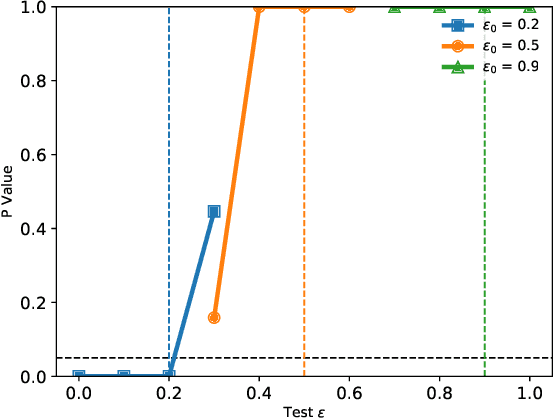
The study of phase transition behaviour in SAT has led to deeper understanding and algorithmic improvements of modern SAT solvers. Motivated by these prior studies of phase transitions in SAT, we seek to study the behaviour of size and compile-time behaviour for random k-CNF formulas in the context of knowledge compilation. We perform a rigorous empirical study and analysis of the size and runtime behavior for different knowledge compilation forms (and their corresponding compilation algorithms): d-DNNFs, SDDs and OBDDs across multiple tools and compilation algorithms. We employ instances generated from the random k-CNF model with varying generation parameters to empirically reason about the expected and median behavior of size and compilation-time for these languages. Our work is similar in spirit to the early work in CSP community on phase transition behavior in SAT/CSP. In a similar spirit, we identify the interesting behavior with respect to different parameters: clause density and solution density, a novel control parameter that we identify for the study of phase transition behavior in the context of knowledge compilation. Furthermore, we summarize our empirical study in terms of two concrete conjectures; a rigorous study of these conjectures will possibly require new theoretical tools.

Manthan: A Data Driven Approach for Boolean Function Synthesis

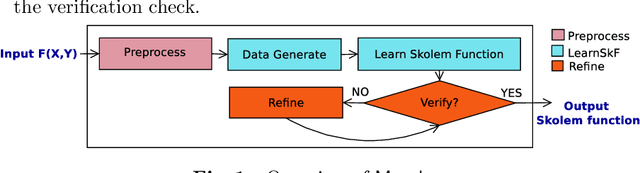
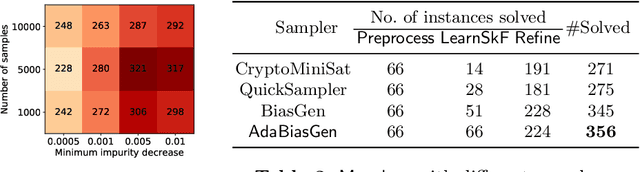
Boolean functional synthesis is a fundamental problem in computer science with wide-ranging applications and has witnessed a surge of interest resulting in progressively improved techniques over the past decade. Despite intense algorithmic development, a large number of problems remain beyond the reach of the state of the art techniques. Motivated by the progress in machine learning, we propose Manthan, a novel data-driven approach to Boolean functional synthesis. Manthan views functional synthesis as a classification problem, relying on advances in constrained sampling for data generation, and advances in automated reasoning for a novel proof-guided refinement and provable verification. On an extensive and rigorous evaluation over 609 benchmarks, we demonstrate that Manthan significantly improves upon the current state of the art, solving 356 benchmarks in comparison to 280, which is the most solved by a state of the art technique; thereby, we demonstrate an increase of 76 benchmarks over the current state of the art. Furthermore, Manthan solves 60 benchmarks that none of the current state of the art techniques could solve. The significant performance improvements, along with our detailed analysis, highlights several interesting avenues of future work at the intersection of machine learning, constrained sampling, and automated reasoning.