Inductive Generalization in Reinforcement Learning from Specifications

We present a novel inductive generalization framework for RL from logical specifications. Many interesting tasks in RL environments have a natural inductive structure. These inductive tasks have similar overarching goals but they differ inductively in low-level predicates and distributions. We present a generalization procedure that leverages this inductive relationship to learn a higher-order function, a policy generator, that generates appropriately adapted policies for instances of an inductive task in a zero-shot manner. An evaluation of the proposed approach on a set of challenging control benchmarks demonstrates the promise of our framework in generalizing to unseen policies for long-horizon tasks.

Generalization for multiclass classification with overparameterized linear models

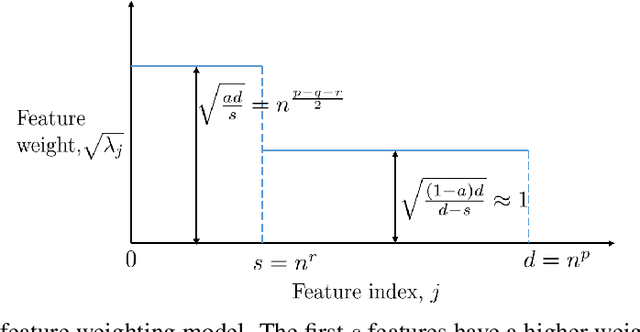
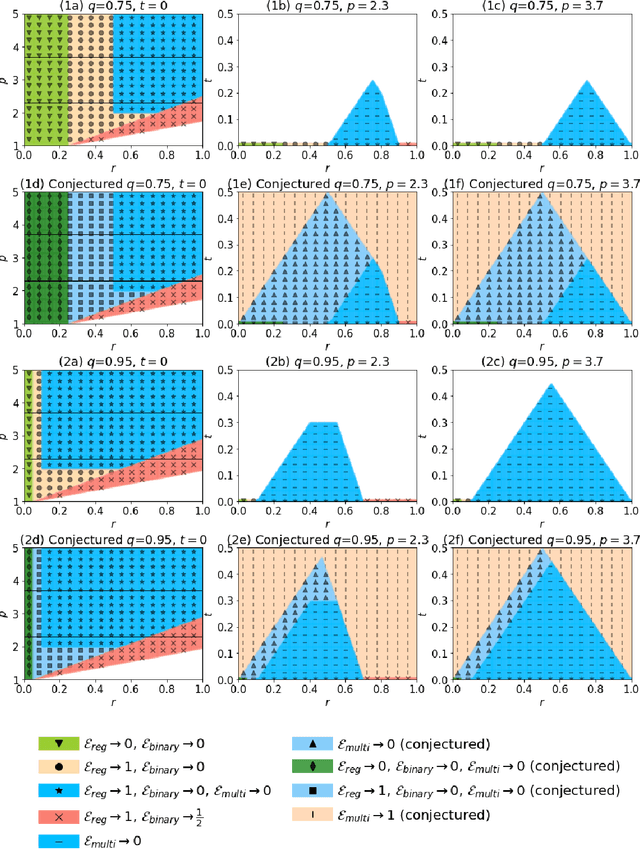
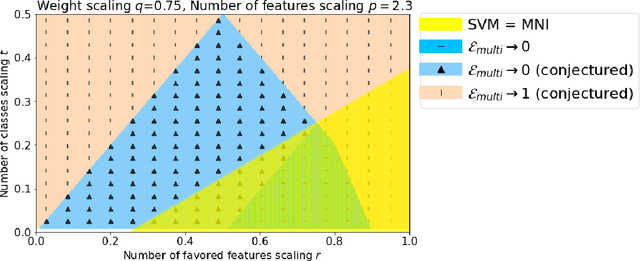
Via an overparameterized linear model with Gaussian features, we provide conditions for good generalization for multiclass classification of minimum-norm interpolating solutions in an asymptotic setting where both the number of underlying features and the number of classes scale with the number of training points. The survival/contamination analysis framework for understanding the behavior of overparameterized learning problems is adapted to this setting, revealing that multiclass classification qualitatively behaves like binary classification in that, as long as there are not too many classes (made precise in the paper), it is possible to generalize well even in some settings where the corresponding regression tasks would not generalize. Besides various technical challenges, it turns out that the key difference from the binary classification setting is that there are relatively fewer positive training examples of each class in the multiclass setting as the number of classes increases, making the multiclass problem "harder" than the binary one.

Classification vs regression in overparameterized regimes: Does the loss function matter?

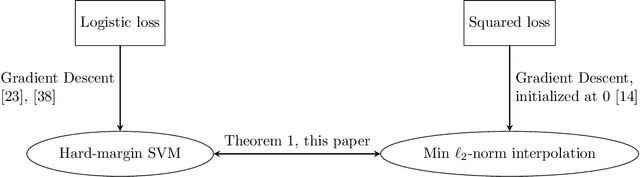
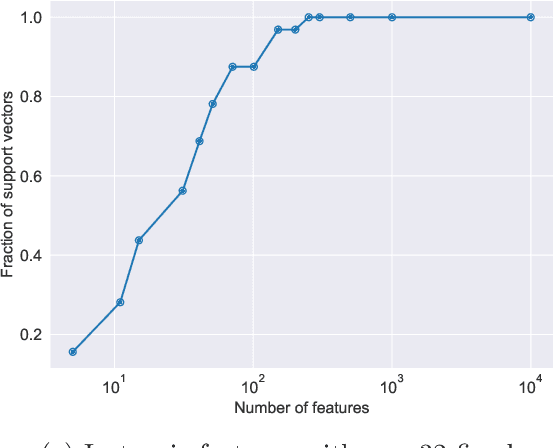
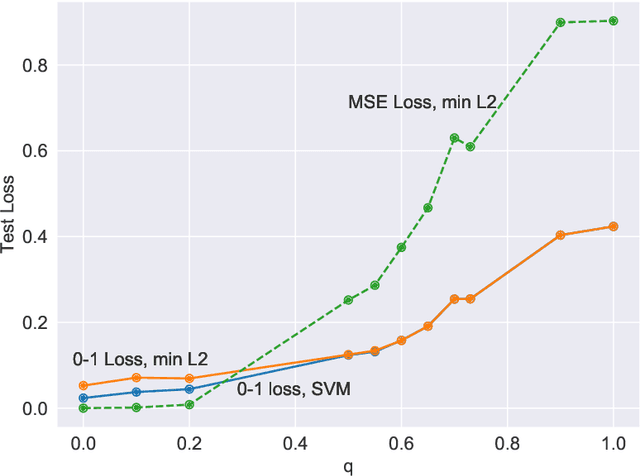
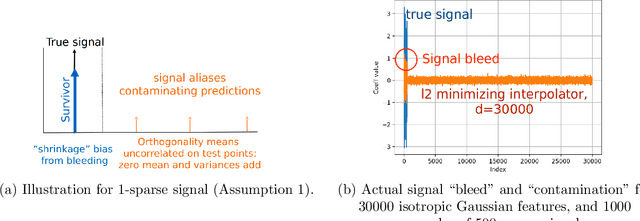
We compare classification and regression tasks in the overparameterized linear model with Gaussian features. On the one hand, we show that with sufficient overparameterization all training points are support vectors: solutions obtained by least-squares minimum-norm interpolation, typically used for regression, are identical to those produced by the hard-margin support vector machine (SVM) that minimizes the hinge loss, typically used for training classifiers. On the other hand, we show that there exist regimes where these solutions are near-optimal when evaluated by the 0-1 test loss function, but do not generalize if evaluated by the square loss function, i.e. they achieve the null risk. Our results demonstrate the very different roles and properties of loss functions used at the training phase (optimization) and the testing phase (generalization).