Inductive Generalization in Reinforcement Learning from Specifications

We present a novel inductive generalization framework for RL from logical specifications. Many interesting tasks in RL environments have a natural inductive structure. These inductive tasks have similar overarching goals but they differ inductively in low-level predicates and distributions. We present a generalization procedure that leverages this inductive relationship to learn a higher-order function, a policy generator, that generates appropriately adapted policies for instances of an inductive task in a zero-shot manner. An evaluation of the proposed approach on a set of challenging control benchmarks demonstrates the promise of our framework in generalizing to unseen policies for long-horizon tasks.

On Strategies in Synthesis Over Finite Traces

The innovations in reactive synthesis from {\em Linear Temporal Logics over finite traces} (LTLf) will be amplified by the ability to verify the correctness of the strategies generated by LTLf synthesis tools. This motivates our work on {\em LTLf model checking}. LTLf model checking, however, is not straightforward. The strategies generated by LTLf synthesis may be represented using {\em terminating} transducers or {\em non-terminating} transducers where executions are of finite-but-unbounded length or infinite length, respectively. For synthesis, there is no evidence that one type of transducer is better than the other since they both demonstrate the same complexity and similar algorithms. In this work, we show that for model checking, the two types of transducers are fundamentally different. Our central result is that LTLf model checking of non-terminating transducers is \emph{exponentially harder} than that of terminating transducers. We show that the problems are EXPSPACE-complete and PSPACE-complete, respectively. Hence, considering the feasibility of verification, LTLf synthesis tools should synthesize terminating transducers. This is, to the best of our knowledge, the \emph{first} evidence to use one transducer over the other in LTLf synthesis.

Specification-Guided Learning of Nash Equilibria with High Social Welfare

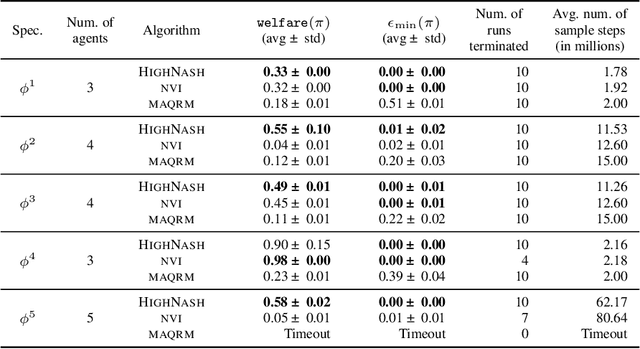
Reinforcement learning has been shown to be an effective strategy for automatically training policies for challenging control problems. Focusing on non-cooperative multi-agent systems, we propose a novel reinforcement learning framework for training joint policies that form a Nash equilibrium. In our approach, rather than providing low-level reward functions, the user provides high-level specifications that encode the objective of each agent. Then, guided by the structure of the specifications, our algorithm searches over policies to identify one that provably forms an $\epsilon$-Nash equilibrium (with high probability). Importantly, it prioritizes policies in a way that maximizes social welfare across all agents. Our empirical evaluation demonstrates that our algorithm computes equilibrium policies with high social welfare, whereas state-of-the-art baselines either fail to compute Nash equilibria or compute ones with comparatively lower social welfare.

Synthesis from Satisficing and Temporal Goals

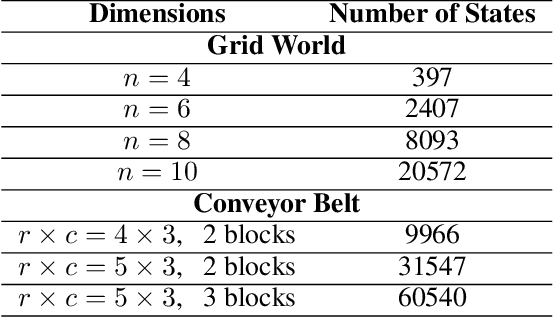
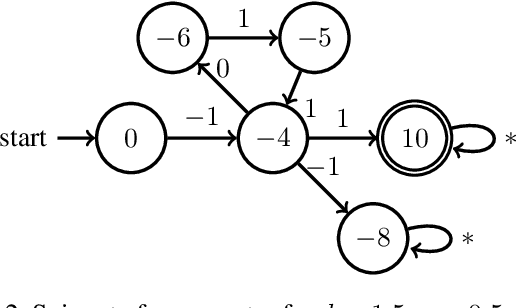
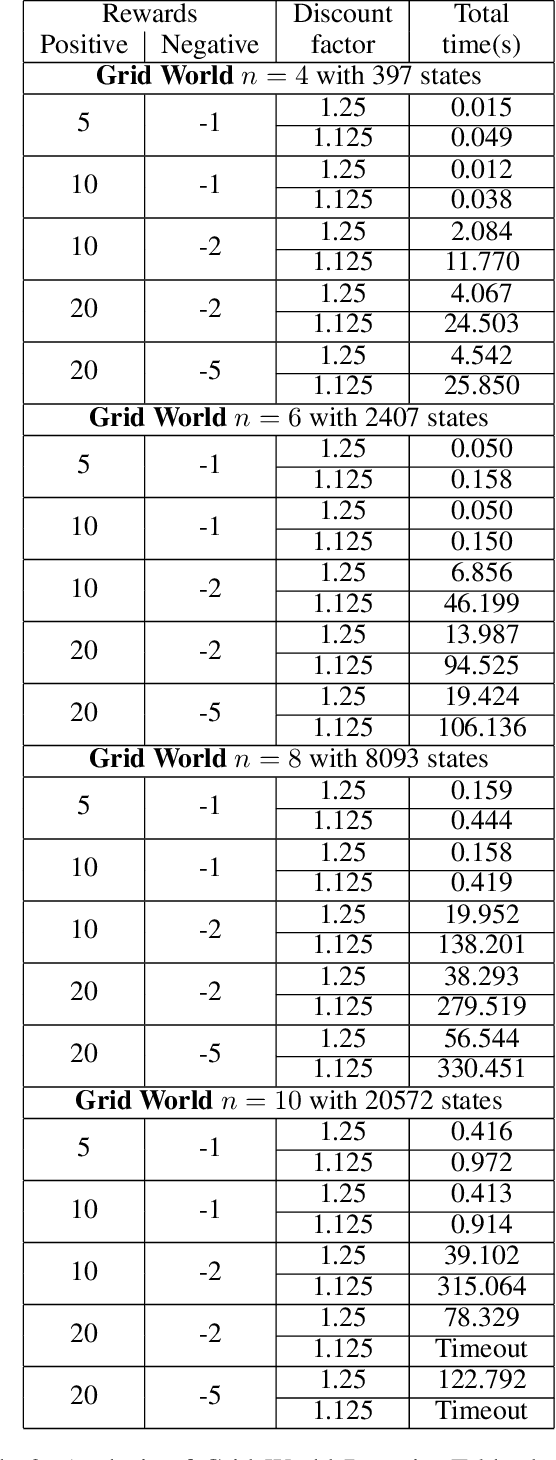
Reactive synthesis from high-level specifications that combine hard constraints expressed in Linear Temporal Logic LTL with soft constraints expressed by discounted-sum (DS) rewards has applications in planning and reinforcement learning. An existing approach combines techniques from LTL synthesis with optimization for the DS rewards but has failed to yield a sound algorithm. An alternative approach combining LTL synthesis with satisficing DS rewards (rewards that achieve a threshold) is sound and complete for integer discount factors, but, in practice, a fractional discount factor is desired. This work extends the existing satisficing approach, presenting the first sound algorithm for synthesis from LTL and DS rewards with fractional discount factors. The utility of our algorithm is demonstrated on robotic planning domains.

Compositional Reinforcement Learning from Logical Specifications

We study the problem of learning control policies for complex tasks given by logical specifications. Recent approaches automatically generate a reward function from a given specification and use a suitable reinforcement learning algorithm to learn a policy that maximizes the expected reward. These approaches, however, scale poorly to complex tasks that require high-level planning. In this work, we develop a compositional learning approach, called DiRL, that interleaves high-level planning and reinforcement learning. First, DiRL encodes the specification as an abstract graph; intuitively, vertices and edges of the graph correspond to regions of the state space and simpler sub-tasks, respectively. Our approach then incorporates reinforcement learning to learn neural network policies for each edge (sub-task) within a Dijkstra-style planning algorithm to compute a high-level plan in the graph. An evaluation of the proposed approach on a set of challenging control benchmarks with continuous state and action spaces demonstrates that it outperforms state-of-the-art baselines.

On Satisficing in Quantitative Games

Several problems in planning and reactive synthesis can be reduced to the analysis of two-player quantitative graph games. {\em Optimization} is one form of analysis. We argue that in many cases it may be better to replace the optimization problem with the {\em satisficing problem}, where instead of searching for optimal solutions, the goal is to search for solutions that adhere to a given threshold bound. This work defines and investigates the satisficing problem on a two-player graph game with the discounted-sum cost model. We show that while the satisficing problem can be solved using numerical methods just like the optimization problem, this approach does not render compelling benefits over optimization. When the discount factor is, however, an integer, we present another approach to satisficing, which is purely based on automata methods. We show that this approach is algorithmically more performant -- both theoretically and empirically -- and demonstrates the broader applicability of satisficing overoptimization.

Hybrid Compositional Reasoning for Reactive Synthesis from Finite-Horizon Specifications

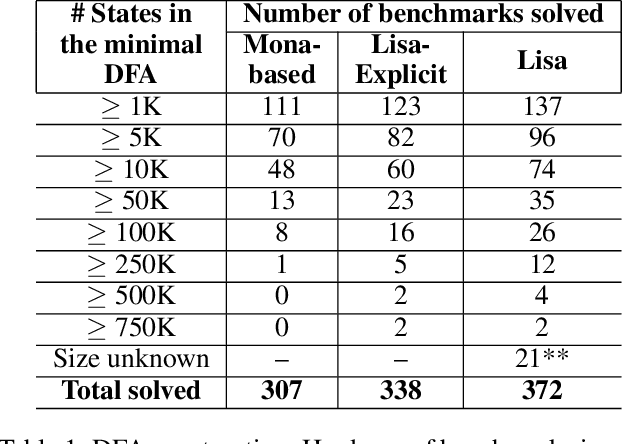
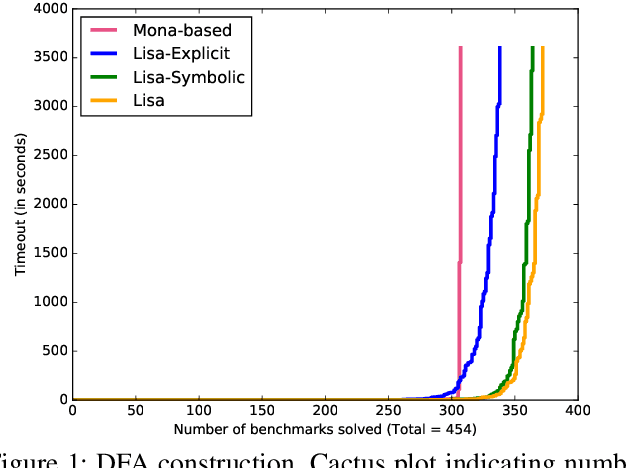
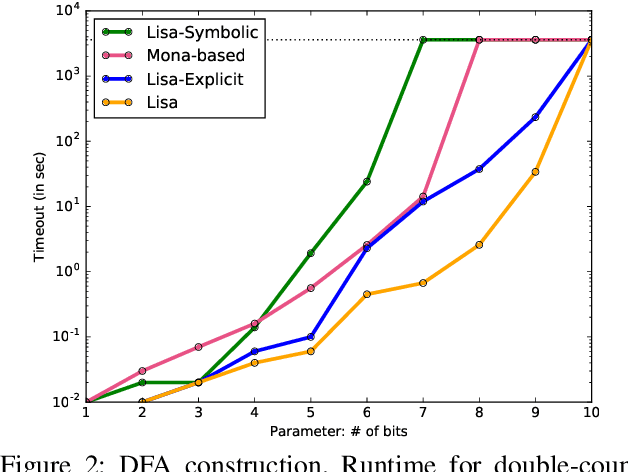
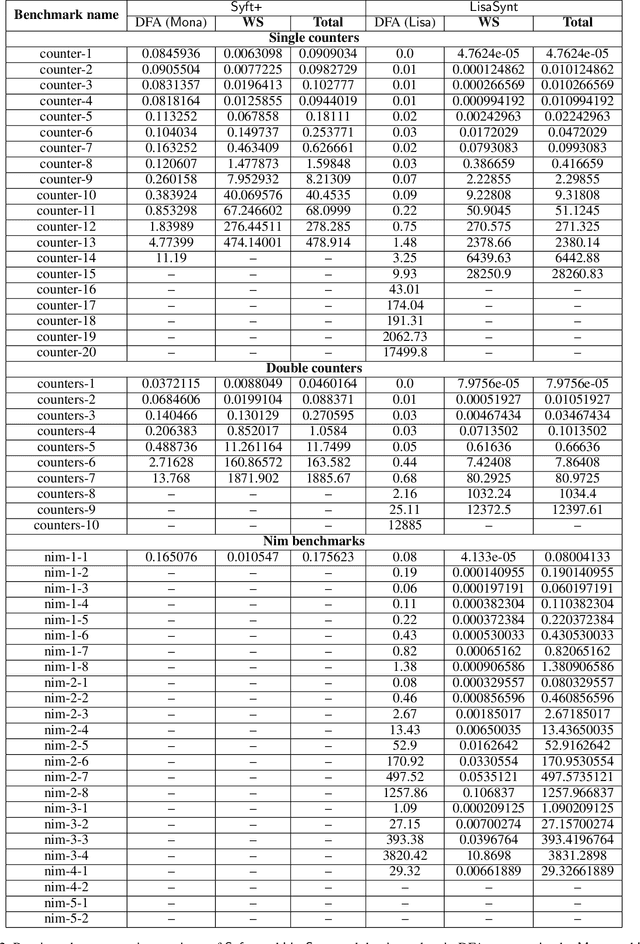
LTLf synthesis is the automated construction of a reactive system from a high-level description, expressed in LTLf, of its finite-horizon behavior. So far, the conversion of LTLf formulas to deterministic finite-state automata (DFAs) has been identified as the primary bottleneck to the scalabity of synthesis. Recent investigations have also shown that the size of the DFA state space plays a critical role in synthesis as well. Therefore, effective resolution of the bottleneck for synthesis requires the conversion to be time and memory performant, and prevent state-space explosion. Current conversion approaches, however, which are based either on explicit-state representation or symbolic-state representation, fail to address these necessities adequately at scale: Explicit-state approaches generate minimal DFA but are slow due to expensive DFA minimization. Symbolic-state representations can be succinct, but due to the lack of DFA minimization they generate such large state spaces that even their symbolic representations cannot compensate for the blow-up. This work proposes a hybrid representation approach for the conversion. Our approach utilizes both explicit and symbolic representations of the state-space, and effectively leverages their complementary strengths. In doing so, we offer an LTLf to DFA conversion technique that addresses all three necessities, hence resolving the bottleneck. A comprehensive empirical evaluation on conversion and synthesis benchmarks supports the merits of our hybrid approach.