Andrew Wells
On Strategies in Synthesis Over Finite Traces
May 20, 2023Abstract:The innovations in reactive synthesis from {\em Linear Temporal Logics over finite traces} (LTLf) will be amplified by the ability to verify the correctness of the strategies generated by LTLf synthesis tools. This motivates our work on {\em LTLf model checking}. LTLf model checking, however, is not straightforward. The strategies generated by LTLf synthesis may be represented using {\em terminating} transducers or {\em non-terminating} transducers where executions are of finite-but-unbounded length or infinite length, respectively. For synthesis, there is no evidence that one type of transducer is better than the other since they both demonstrate the same complexity and similar algorithms. In this work, we show that for model checking, the two types of transducers are fundamentally different. Our central result is that LTLf model checking of non-terminating transducers is \emph{exponentially harder} than that of terminating transducers. We show that the problems are EXPSPACE-complete and PSPACE-complete, respectively. Hence, considering the feasibility of verification, LTLf synthesis tools should synthesize terminating transducers. This is, to the best of our knowledge, the \emph{first} evidence to use one transducer over the other in LTLf synthesis.
Synthesis from Satisficing and Temporal Goals
May 20, 2022
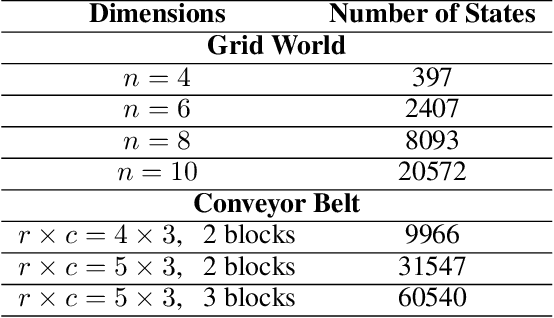
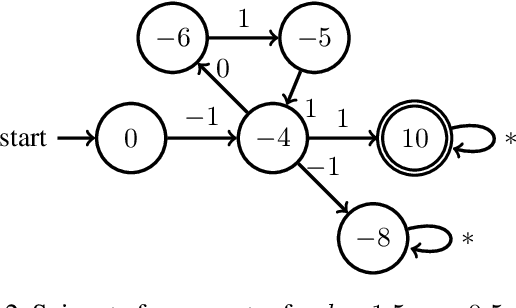
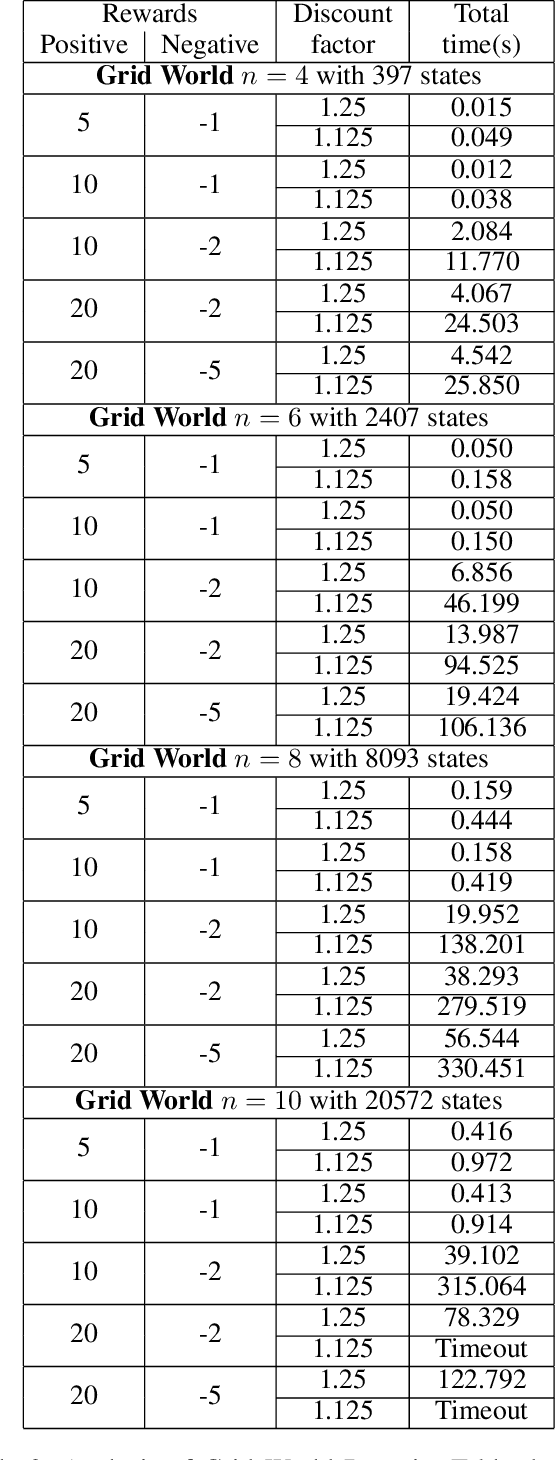
Abstract:Reactive synthesis from high-level specifications that combine hard constraints expressed in Linear Temporal Logic LTL with soft constraints expressed by discounted-sum (DS) rewards has applications in planning and reinforcement learning. An existing approach combines techniques from LTL synthesis with optimization for the DS rewards but has failed to yield a sound algorithm. An alternative approach combining LTL synthesis with satisficing DS rewards (rewards that achieve a threshold) is sound and complete for integer discount factors, but, in practice, a fractional discount factor is desired. This work extends the existing satisficing approach, presenting the first sound algorithm for synthesis from LTL and DS rewards with fractional discount factors. The utility of our algorithm is demonstrated on robotic planning domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge