Value Iteration with Guessing for Markov Chains and Markov Decision Processes

Two standard models for probabilistic systems are Markov chains (MCs) and Markov decision processes (MDPs). Classic objectives for such probabilistic models for control and planning problems are reachability and stochastic shortest path. The widely studied algorithmic approach for these problems is the Value Iteration (VI) algorithm which iteratively applies local updates called Bellman updates. There are many practical approaches for VI in the literature but they all require exponentially many Bellman updates for MCs in the worst case. A preprocessing step is an algorithm that is discrete, graph-theoretical, and requires linear space. An important open question is whether, after a polynomial-time preprocessing, VI can be achieved with sub-exponentially many Bellman updates. In this work, we present a new approach for VI based on guessing values. Our theoretical contributions are twofold. First, for MCs, we present an almost-linear-time preprocessing algorithm after which, along with guessing values, VI requires only subexponentially many Bellman updates. Second, we present an improved analysis of the speed of convergence of VI for MDPs. Finally, we present a practical algorithm for MDPs based on our new approach. Experimental results show that our approach provides a considerable improvement over existing VI-based approaches on several benchmark examples from the literature.

Qualitative Analysis of $ω$-Regular Objectives on Robust MDPs

Robust Markov Decision Processes (RMDPs) generalize classical MDPs that consider uncertainties in transition probabilities by defining a set of possible transition functions. An objective is a set of runs (or infinite trajectories) of the RMDP, and the value for an objective is the maximal probability that the agent can guarantee against the adversarial environment. We consider (a) reachability objectives, where given a target set of states, the goal is to eventually arrive at one of them; and (b) parity objectives, which are a canonical representation for $\omega$-regular objectives. The qualitative analysis problem asks whether the objective can be ensured with probability 1. In this work, we study the qualitative problem for reachability and parity objectives on RMDPs without making any assumption over the structures of the RMDPs, e.g., unichain or aperiodic. Our contributions are twofold. We first present efficient algorithms with oracle access to uncertainty sets that solve qualitative problems of reachability and parity objectives. We then report experimental results demonstrating the effectiveness of our oracle-based approach on classical RMDP examples from the literature scaling up to thousands of states.

Quantified Linear and Polynomial Arithmetic Satisfiability via Template-based Skolemization

The problem of checking satisfiability of linear real arithmetic (LRA) and non-linear real arithmetic (NRA) formulas has broad applications, in particular, they are at the heart of logic-related applications such as logic for artificial intelligence, program analysis, etc. While there has been much work on checking satisfiability of unquantified LRA and NRA formulas, the problem of checking satisfiability of quantified LRA and NRA formulas remains a significant challenge. The main bottleneck in the existing methods is a computationally expensive quantifier elimination step. In this work, we propose a novel method for efficient quantifier elimination in quantified LRA and NRA formulas. We propose a template-based Skolemization approach, where we automatically synthesize linear/polynomial Skolem functions in order to eliminate quantifiers in the formula. The key technical ingredients in our approach are Positivstellens\"atze theorems from algebraic geometry, which allow for an efficient manipulation of polynomial inequalities. Our method offers a range of appealing theoretical properties combined with a strong practical performance. On the theory side, our method is sound, semi-complete, and runs in subexponential time and polynomial space, as opposed to existing sound and complete quantifier elimination methods that run in doubly-exponential time and at least exponential space. On the practical side, our experiments show superior performance compared to state-of-the-art SMT solvers in terms of the number of solved instances and runtime, both on LRA and on NRA benchmarks.

Linear Equations with Min and Max Operators: Computational Complexity

We consider a class of optimization problems defined by a system of linear equations with min and max operators. This class of optimization problems has been studied under restrictive conditions, such as, (C1) the halting or stability condition; (C2) the non-negative coefficients condition; (C3) the sum up to 1 condition; and (C4) the only min or only max oerator condition. Several seminal results in the literature focus on special cases. For example, turn-based stochastic games correspond to conditions C2 and C3; and Markov decision process to conditions C2, C3, and C4. However, the systematic computational complexity study of all the cases has not been explored, which we address in this work. Some highlights of our results are: with conditions C2 and C4, and with conditions C3 and C4, the problem is NP-complete, whereas with condition C1 only, the problem is in UP intersects coUP. Finally, we establish the computational complexity of the decision problem of checking the respective conditions.

Certified Policy Verification and Synthesis for MDPs under Distributional Reach-avoidance Properties

Markov Decision Processes (MDPs) are a classical model for decision making in the presence of uncertainty. Often they are viewed as state transformers with planning objectives defined with respect to paths over MDP states. An increasingly popular alternative is to view them as distribution transformers, giving rise to a sequence of probability distributions over MDP states. For instance, reachability and safety properties in modeling robot swarms or chemical reaction networks are naturally defined in terms of probability distributions over states. Verifying such distributional properties is known to be hard and often beyond the reach of classical state-based verification techniques. In this work, we consider the problems of certified policy (i.e. controller) verification and synthesis in MDPs under distributional reach-avoidance specifications. By certified we mean that, along with a policy, we also aim to synthesize a (checkable) certificate ensuring that the MDP indeed satisfies the property. Thus, given the target set of distributions and an unsafe set of distributions over MDP states, our goal is to either synthesize a certificate for a given policy or synthesize a policy along with a certificate, proving that the target distribution can be reached while avoiding unsafe distributions. To solve this problem, we introduce the novel notion of distributional reach-avoid certificates and present automated procedures for (1) synthesizing a certificate for a given policy, and (2) synthesizing a policy together with the certificate, both providing formal guarantees on certificate correctness. Our experimental evaluation demonstrates the ability of our method to solve several non-trivial examples, including a multi-agent robot-swarm model, to synthesize certified policies and to certify existing policies.

Learning Algorithms for Verification of Markov Decision Processes

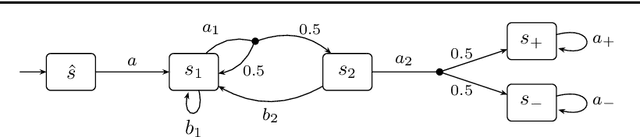
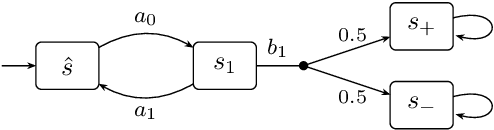
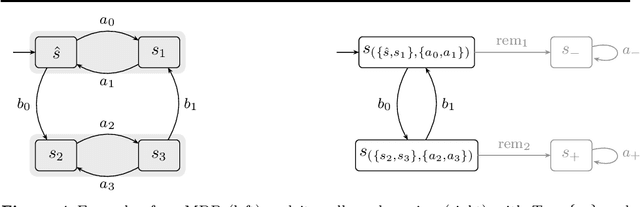
We present a general framework for applying learning algorithms and heuristical guidance to the verification of Markov decision processes (MDPs). The primary goal of our techniques is to improve performance by avoiding an exhaustive exploration of the state space, instead focussing on particularly relevant areas of the system, guided by heuristics. Our work builds on the previous results of Br{\'{a}}zdil et al., significantly extending it as well as refining several details and fixing errors. The presented framework focuses on probabilistic reachability, which is a core problem in verification, and is instantiated in two distinct scenarios. The first assumes that full knowledge of the MDP is available, in particular precise transition probabilities. It performs a heuristic-driven partial exploration of the model, yielding precise lower and upper bounds on the required probability. The second tackles the case where we may only sample the MDP without knowing the exact transition dynamics. Here, we obtain probabilistic guarantees, again in terms of both the lower and upper bounds, which provides efficient stopping criteria for the approximation. In particular, the latter is an extension of statistical model-checking (SMC) for unbounded properties in MDPs. In contrast to other related approaches, we do not restrict our attention to time-bounded (finite-horizon) or discounted properties, nor assume any particular structural properties of the MDP.

Solving Long-run Average Reward Robust MDPs via Stochastic Games

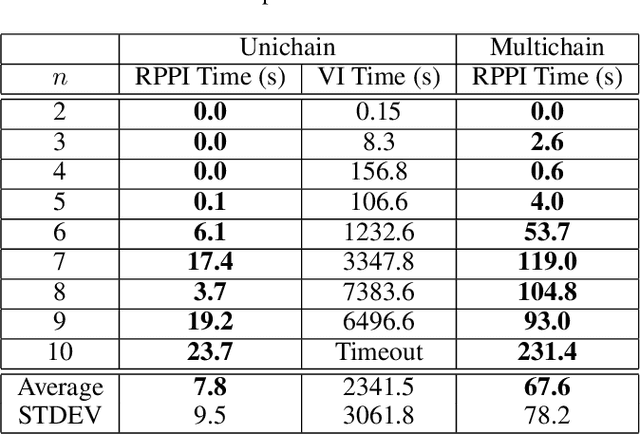
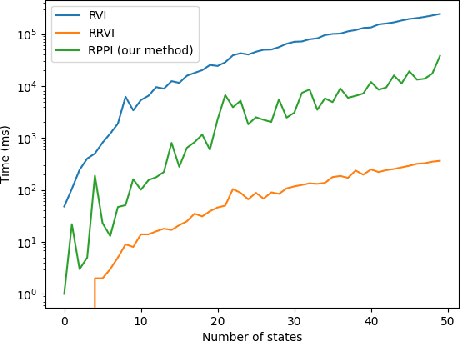
Markov decision processes (MDPs) provide a standard framework for sequential decision making under uncertainty. However, transition probabilities in MDPs are often estimated from data and MDPs do not take data uncertainty into account. Robust Markov decision processes (RMDPs) address this shortcoming of MDPs by assigning to each transition an uncertainty set rather than a single probability value. The goal of solving RMDPs is then to find a policy which maximizes the worst-case performance over the uncertainty sets. In this work, we consider polytopic RMDPs in which all uncertainty sets are polytopes and study the problem of solving long-run average reward polytopic RMDPs. Our focus is on computational complexity aspects and efficient algorithms. We present a novel perspective on this problem and show that it can be reduced to solving long-run average reward turn-based stochastic games with finite state and action spaces. This reduction allows us to derive several important consequences that were hitherto not known to hold for polytopic RMDPs. First, we derive new computational complexity bounds for solving long-run average reward polytopic RMDPs, showing for the first time that the threshold decision problem for them is in NP coNP and that they admit a randomized algorithm with sub-exponential expected runtime. Second, we present Robust Polytopic Policy Iteration (RPPI), a novel policy iteration algorithm for solving long-run average reward polytopic RMDPs. Our experimental evaluation shows that RPPI is much more efficient in solving long-run average reward polytopic RMDPs compared to state-of-the-art methods based on value iteration.

Compositional Policy Learning in Stochastic Control Systems with Formal Guarantees

Reinforcement learning has shown promising results in learning neural network policies for complicated control tasks. However, the lack of formal guarantees about the behavior of such policies remains an impediment to their deployment. We propose a novel method for learning a composition of neural network policies in stochastic environments, along with a formal certificate which guarantees that a specification over the policy's behavior is satisfied with the desired probability. Unlike prior work on verifiable RL, our approach leverages the compositional nature of logical specifications provided in SpectRL, to learn over graphs of probabilistic reach-avoid specifications. The formal guarantees are provided by learning neural network policies together with reach-avoid supermartingales (RASM) for the graph's sub-tasks and then composing them into a global policy. We also derive a tighter lower bound compared to previous work on the probability of reach-avoidance implied by a RASM, which is required to find a compositional policy with an acceptable probabilistic threshold for complex tasks with multiple edge policies. We implement a prototype of our approach and evaluate it on a Stochastic Nine Rooms environment.

Quantization-aware Interval Bound Propagation for Training Certifiably Robust Quantized Neural Networks

We study the problem of training and certifying adversarially robust quantized neural networks (QNNs). Quantization is a technique for making neural networks more efficient by running them using low-bit integer arithmetic and is therefore commonly adopted in industry. Recent work has shown that floating-point neural networks that have been verified to be robust can become vulnerable to adversarial attacks after quantization, and certification of the quantized representation is necessary to guarantee robustness. In this work, we present quantization-aware interval bound propagation (QA-IBP), a novel method for training robust QNNs. Inspired by advances in robust learning of non-quantized networks, our training algorithm computes the gradient of an abstract representation of the actual network. Unlike existing approaches, our method can handle the discrete semantics of QNNs. Based on QA-IBP, we also develop a complete verification procedure for verifying the adversarial robustness of QNNs, which is guaranteed to terminate and produce a correct answer. Compared to existing approaches, the key advantage of our verification procedure is that it runs entirely on GPU or other accelerator devices. We demonstrate experimentally that our approach significantly outperforms existing methods and establish the new state-of-the-art for training and certifying the robustness of QNNs.

Learning Control Policies for Region Stabilization in Stochastic Systems

We consider the problem of learning control policies in stochastic systems which guarantee that the system stabilizes within some specified stabilization region with probability $1$. Our approach is based on the novel notion of stabilizing ranking supermartingales (sRSMs) that we introduce in this work. Our sRSMs overcome the limitation of methods proposed in previous works whose applicability is restricted to systems in which the stabilizing region cannot be left once entered under any control policy. We present a learning procedure that learns a control policy together with an sRSM that formally certifies probability-$1$ stability, both learned as neural networks. Our experimental evaluation shows that our learning procedure can successfully learn provably stabilizing policies in practice.