Robust Verification of Concurrent Stochastic Games

Autonomous systems often operate in multi-agent settings and need to make concurrent, strategic decisions, typically in uncertain environments. Verification and control problems for these systems can be tackled with concurrent stochastic games (CSGs), but this model requires transition probabilities to be precisely specified - an unrealistic requirement in many real-world settings. We introduce *robust CSGs* and their subclass *interval CSGs* (ICSGs), which capture epistemic uncertainty about transition probabilities in CSGs. We propose a novel framework for *robust* verification of these models under worst-case assumptions about transition uncertainty. Specifically, we develop the underlying theoretical foundations and efficient algorithms, for finite- and infinite-horizon objectives in both zero-sum and nonzero-sum settings, the latter based on (social-welfare optimal) Nash equilibria. We build an implementation in the PRISM-games model checker and demonstrate the feasibility of robust verification of ICSGs across a selection of large benchmarks.

Multi-Property Synthesis

We study LTLf synthesis with multiple properties, where satisfying all properties may be impossible. Instead of enumerating subsets of properties, we compute in one fixed-point computation the relation between product-game states and the goal sets that are realizable from them, and we synthesize strategies achieving maximal realizable sets. We develop a fully symbolic algorithm that introduces Boolean goal variables and exploits monotonicity to represent exponentially many goal combinations compactly. Our approach substantially outperforms enumeration-based baselines, with speedups of up to two orders of magnitude.

About Time: Model-free Reinforcement Learning with Timed Reward Machines

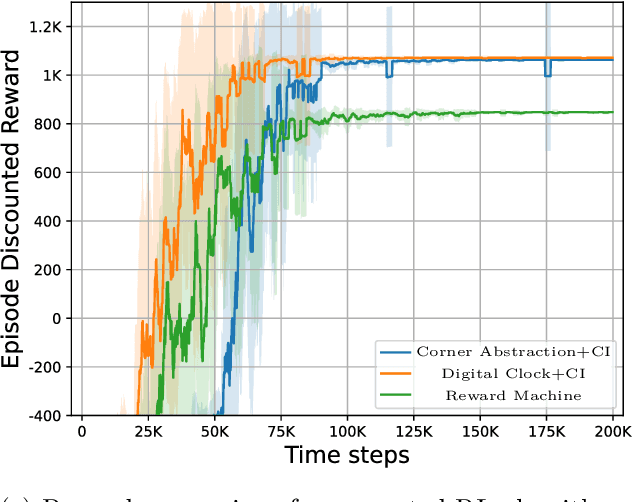
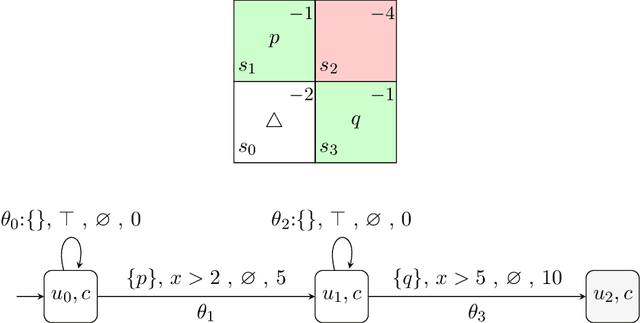
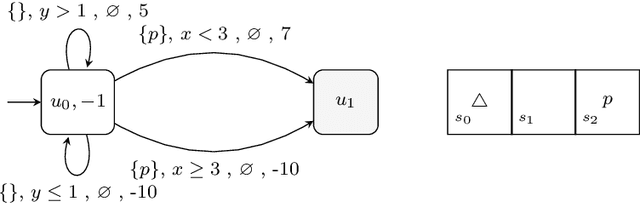
Reward specification plays a central role in reinforcement learning (RL), guiding the agent's behavior. To express non-Markovian rewards, formalisms such as reward machines have been introduced to capture dependencies on histories. However, traditional reward machines lack the ability to model precise timing constraints, limiting their use in time-sensitive applications. In this paper, we propose timed reward machines (TRMs), which are an extension of reward machines that incorporate timing constraints into the reward structure. TRMs enable more expressive specifications with tunable reward logic, for example, imposing costs for delays and granting rewards for timely actions. We study model-free RL frameworks (i.e., tabular Q-learning) for learning optimal policies with TRMs under digital and real-time semantics. Our algorithms integrate the TRM into learning via abstractions of timed automata, and employ counterfactual-imagining heuristics that exploit the structure of the TRM to improve the search. Experimentally, we demonstrate that our algorithm learns policies that achieve high rewards while satisfying the timing constraints specified by the TRM on popular RL benchmarks. Moreover, we conduct comparative studies of performance under different TRM semantics, along with ablations that highlight the benefits of counterfactual-imagining.

Efficient Solution and Learning of Robust Factored MDPs

Robust Markov decision processes (r-MDPs) extend MDPs by explicitly modelling epistemic uncertainty about transition dynamics. Learning r-MDPs from interactions with an unknown environment enables the synthesis of robust policies with provable (PAC) guarantees on performance, but this can require a large number of sample interactions. We propose novel methods for solving and learning r-MDPs based on factored state-space representations that leverage the independence between model uncertainty across system components. Although policy synthesis for factored r-MDPs leads to hard, non-convex optimisation problems, we show how to reformulate these into tractable linear programs. Building on these, we also propose methods to learn factored model representations directly. Our experimental results show that exploiting factored structure can yield dimensional gains in sample efficiency, producing more effective robust policies with tighter performance guarantees than state-of-the-art methods.

Learning Probabilistic Temporal Logic Specifications for Stochastic Systems

There has been substantial progress in the inference of formal behavioural specifications from sample trajectories, for example, using Linear Temporal Logic (LTL). However, these techniques cannot handle specifications that correctly characterise systems with stochastic behaviour, which occur commonly in reinforcement learning and formal verification. We consider the passive learning problem of inferring a Boolean combination of probabilistic LTL (PLTL) formulas from a set of Markov chains, classified as either positive or negative. We propose a novel learning algorithm that infers concise PLTL specifications, leveraging grammar-based enumeration, search heuristics, probabilistic model checking and Boolean set-cover procedures. We demonstrate the effectiveness of our algorithm in two use cases: learning from policies induced by RL algorithms and learning from variants of a probabilistic model. In both cases, our method automatically and efficiently extracts PLTL specifications that succinctly characterise the temporal differences between the policies or model variants.

Planning with Linear Temporal Logic Specifications: Handling Quantifiable and Unquantifiable Uncertainty

This work studies the planning problem for robotic systems under both quantifiable and unquantifiable uncertainty. The objective is to enable the robotic systems to optimally fulfill high-level tasks specified by Linear Temporal Logic (LTL) formulas. To capture both types of uncertainty in a unified modelling framework, we utilise Markov Decision Processes with Set-valued Transitions (MDPSTs). We introduce a novel solution technique for the optimal robust strategy synthesis of MDPSTs with LTL specifications. To improve efficiency, our work leverages limit-deterministic B\"uchi automata (LDBAs) as the automaton representation for LTL to take advantage of their efficient constructions. To tackle the inherent nondeterminism in MDPSTs, which presents a significant challenge for reducing the LTL planning problem to a reachability problem, we introduce the concept of a Winning Region (WR) for MDPSTs. Additionally, we propose an algorithm for computing the WR over the product of the MDPST and the LDBA. Finally, a robust value iteration algorithm is invoked to solve the reachability problem. We validate the effectiveness of our approach through a case study involving a mobile robot operating in the hexagonal world, demonstrating promising efficiency gains.

Robust Markov Decision Processes: A Place Where AI and Formal Methods Meet

Markov decision processes (MDPs) are a standard model for sequential decision-making problems and are widely used across many scientific areas, including formal methods and artificial intelligence (AI). MDPs do, however, come with the restrictive assumption that the transition probabilities need to be precisely known. Robust MDPs (RMDPs) overcome this assumption by instead defining the transition probabilities to belong to some uncertainty set. We present a gentle survey on RMDPs, providing a tutorial covering their fundamentals. In particular, we discuss RMDP semantics and how to solve them by extending standard MDP methods such as value iteration and policy iteration. We also discuss how RMDPs relate to other models and how they are used in several contexts, including reinforcement learning and abstraction techniques. We conclude with some challenges for future work on RMDPs.

Expectation vs. Reality: Towards Verification of Psychological Games

Game theory provides an effective way to model strategic interactions among rational agents. In the context of formal verification, these ideas can be used to produce guarantees on the correctness of multi-agent systems, with a diverse range of applications from computer security to autonomous driving. Psychological games (PGs) were developed as a way to model and analyse agents with belief-dependent motivations, opening up the possibility to model how human emotions can influence behaviour. In PGs, players' utilities depend not only on what actually happens (which strategies players choose to adopt), but also on what the players had expected to happen (their belief as to the strategies that would be played). Despite receiving much attention in fields such as economics and psychology, very little consideration has been given to their applicability to problems in computer science, nor to practical algorithms and tool support. In this paper, we start to bridge that gap, proposing methods to solve PGs and implementing them within PRISM-games, a formal verification tool for stochastic games. We discuss how to model these games, highlight specific challenges for their analysis and illustrate the usefulness of our approach on several case studies, including human behaviour in traffic scenarios.

Learning Provably Robust Policies in Uncertain Parametric Environments

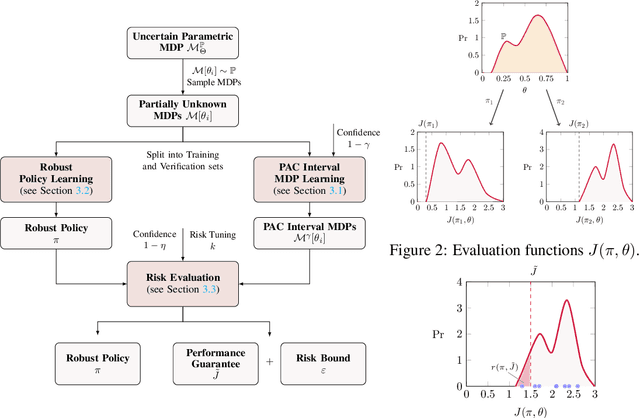
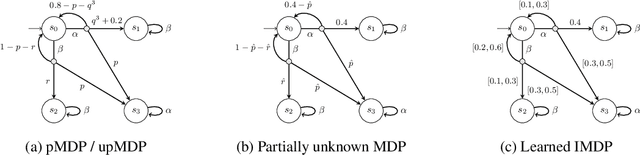
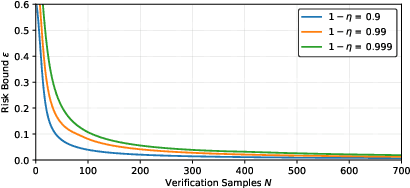
We present a data-driven approach for learning MDP policies that are robust across stochastic environments whose transition probabilities are defined by parameters with an unknown distribution. We produce probably approximately correct (PAC) guarantees for the performance of these learned policies in a new, unseen environment over the unknown distribution. Our approach is based on finite samples of the MDP environments, for each of which we build an approximation of the model as an interval MDP, by exploring a set of generated trajectories. We use the built approximations to synthesise a single policy that performs well (meets given requirements) across the sampled environments, and furthermore bound its risk (of not meeting the given requirements) when deployed in an unseen environment. Our procedure offers a trade-off between the guaranteed performance of the learned policy and the risk of not meeting the guarantee in an unseen environment. Our approach exploits knowledge of the environment's state space and graph structure, and we show how additional knowledge of its parametric structure can be leveraged to optimize learning and to obtain tighter guarantees from less samples. We evaluate our approach on a diverse range of established benchmarks, demonstrating that we can generate highly performing and robust policies, along with guarantees that tightly quantify their performance and the associated risk.

Safe POMDP Online Planning among Dynamic Agents via Adaptive Conformal Prediction

Online planning for partially observable Markov decision processes (POMDPs) provides efficient techniques for robot decision-making under uncertainty. However, existing methods fall short of preventing safety violations in dynamic environments. This work presents a novel safe POMDP online planning approach that offers probabilistic safety guarantees amidst environments populated by multiple dynamic agents. Our approach utilizes data-driven trajectory prediction models of dynamic agents and applies Adaptive Conformal Prediction (ACP) for assessing the uncertainties in these predictions. Leveraging the obtained ACP-based trajectory predictions, our approach constructs safety shields on-the-fly to prevent unsafe actions within POMDP online planning. Through experimental evaluation in various dynamic environments using real-world pedestrian trajectory data, the proposed approach has been shown to effectively maintain probabilistic safety guarantees while accommodating up to hundreds of dynamic agents.