Learning Provably Robust Policies in Uncertain Parametric Environments

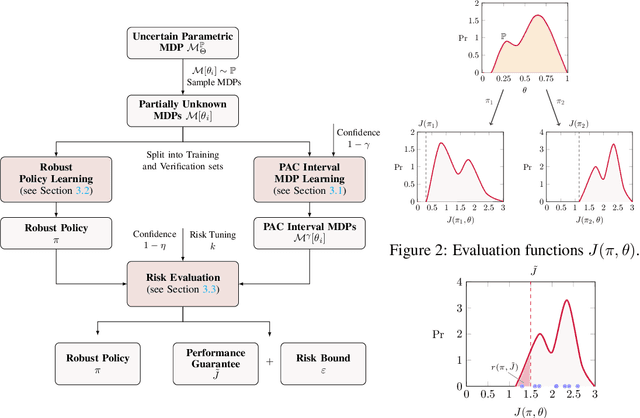
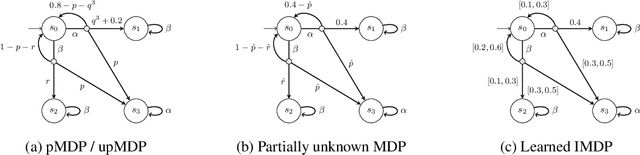
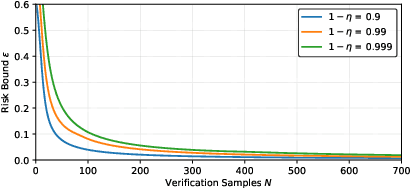
We present a data-driven approach for learning MDP policies that are robust across stochastic environments whose transition probabilities are defined by parameters with an unknown distribution. We produce probably approximately correct (PAC) guarantees for the performance of these learned policies in a new, unseen environment over the unknown distribution. Our approach is based on finite samples of the MDP environments, for each of which we build an approximation of the model as an interval MDP, by exploring a set of generated trajectories. We use the built approximations to synthesise a single policy that performs well (meets given requirements) across the sampled environments, and furthermore bound its risk (of not meeting the given requirements) when deployed in an unseen environment. Our procedure offers a trade-off between the guaranteed performance of the learned policy and the risk of not meeting the guarantee in an unseen environment. Our approach exploits knowledge of the environment's state space and graph structure, and we show how additional knowledge of its parametric structure can be leveraged to optimize learning and to obtain tighter guarantees from less samples. We evaluate our approach on a diverse range of established benchmarks, demonstrating that we can generate highly performing and robust policies, along with guarantees that tightly quantify their performance and the associated risk.