Certified Approximate Reachability (CARe): Formal Error Bounds on Deep Learning of Reachable Sets

Recent approaches to leveraging deep learning for computing reachable sets of continuous-time dynamical systems have gained popularity over traditional level-set methods, as they overcome the curse of dimensionality. However, as with level-set methods, considerable care needs to be taken in limiting approximation errors, particularly since no guarantees are provided during training on the accuracy of the learned reachable set. To address this limitation, we introduce an epsilon-approximate Hamilton-Jacobi Partial Differential Equation (HJ-PDE), which establishes a relationship between training loss and accuracy of the true reachable set. To formally certify this approximation, we leverage Satisfiability Modulo Theories (SMT) solvers to bound the residual error of the HJ-based loss function across the domain of interest. Leveraging Counter Example Guided Inductive Synthesis (CEGIS), we close the loop around learning and verification, by fine-tuning the neural network on counterexamples found by the SMT solver, thus improving the accuracy of the learned reachable set. To the best of our knowledge, Certified Approximate Reachability (CARe) is the first approach to provide soundness guarantees on learned reachable sets of continuous dynamical systems.

Learning Provably Robust Policies in Uncertain Parametric Environments

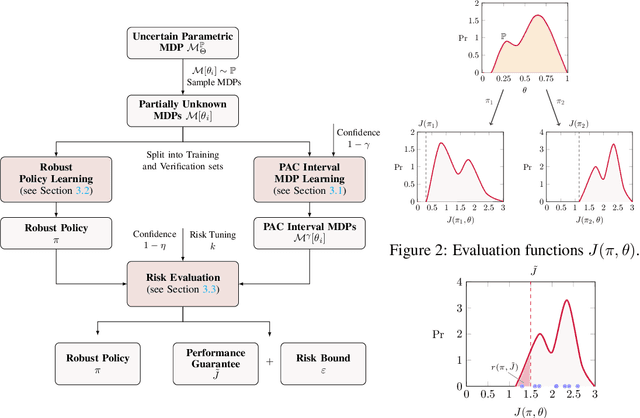
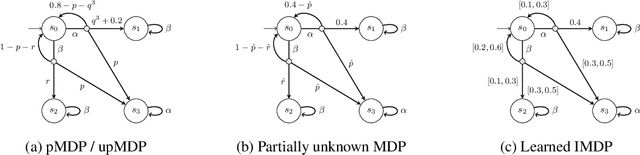
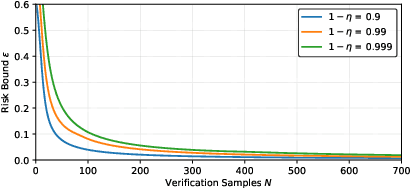
We present a data-driven approach for learning MDP policies that are robust across stochastic environments whose transition probabilities are defined by parameters with an unknown distribution. We produce probably approximately correct (PAC) guarantees for the performance of these learned policies in a new, unseen environment over the unknown distribution. Our approach is based on finite samples of the MDP environments, for each of which we build an approximation of the model as an interval MDP, by exploring a set of generated trajectories. We use the built approximations to synthesise a single policy that performs well (meets given requirements) across the sampled environments, and furthermore bound its risk (of not meeting the given requirements) when deployed in an unseen environment. Our procedure offers a trade-off between the guaranteed performance of the learned policy and the risk of not meeting the guarantee in an unseen environment. Our approach exploits knowledge of the environment's state space and graph structure, and we show how additional knowledge of its parametric structure can be leveraged to optimize learning and to obtain tighter guarantees from less samples. We evaluate our approach on a diverse range of established benchmarks, demonstrating that we can generate highly performing and robust policies, along with guarantees that tightly quantify their performance and the associated risk.

Bisimulation Learning

We introduce a data-driven approach to computing finite bisimulations for state transition systems with very large, possibly infinite state space. Our novel technique computes stutter-insensitive bisimulations of deterministic systems, which we characterize as the problem of learning a state classifier together with a ranking function for each class. Our procedure learns a candidate state classifier and candidate ranking functions from a finite dataset of sample states; then, it checks whether these generalise to the entire state space using satisfiability modulo theory solving. Upon the affirmative answer, the procedure concludes that the classifier constitutes a valid stutter-insensitive bisimulation of the system. Upon a negative answer, the solver produces a counterexample state for which the classifier violates the claim, adds it to the dataset, and repeats learning and checking in a counterexample-guided inductive synthesis loop until a valid bisimulation is found. We demonstrate on a range of benchmarks from reactive verification and software model checking that our method yields faster verification results than alternative state-of-the-art tools in practice. Our method produces succinct abstractions that enable an effective verification of linear temporal logic without next operator, and are interpretable for system diagnostics.