Neural Continuous-Time Supermartingale Certificates

We introduce for the first time a neural-certificate framework for continuous-time stochastic dynamical systems. Autonomous learning systems in the physical world demand continuous-time reasoning, yet existing learnable certificates for probabilistic verification assume discretization of the time continuum. Inspired by the success of training neural Lyapunov certificates for deterministic continuous-time systems and neural supermartingale certificates for stochastic discrete-time systems, we propose a framework that bridges the gap between continuous-time and probabilistic neural certification for dynamical systems under complex requirements. Our method combines machine learning and symbolic reasoning to produce formally certified bounds on the probabilities that a nonlinear system satisfies specifications of reachability, avoidance, and persistence. We present both the theoretical justification and the algorithmic implementation of our framework and showcase its efficacy on popular benchmarks.

Neural Model Checking

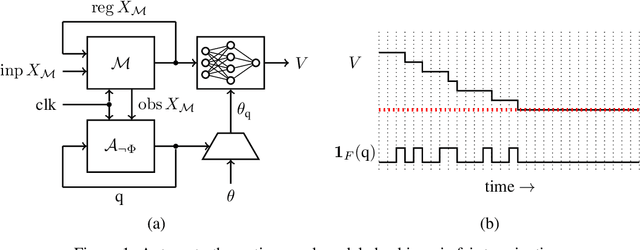
We introduce a machine learning approach to model checking temporal logic, with application to formal hardware verification. Model checking answers the question of whether every execution of a given system satisfies a desired temporal logic specification. Unlike testing, model checking provides formal guarantees. Its application is expected standard in silicon design and the EDA industry has invested decades into the development of performant symbolic model checking algorithms. Our new approach combines machine learning and symbolic reasoning by using neural networks as formal proof certificates for linear temporal logic. We train our neural certificates from randomly generated executions of the system and we then symbolically check their validity using satisfiability solving which, upon the affirmative answer, establishes that the system provably satisfies the specification. We leverage the expressive power of neural networks to represent proof certificates as well as the fact that checking a certificate is much simpler than finding one. As a result, our machine learning procedure for model checking is entirely unsupervised, formally sound, and practically effective. We experimentally demonstrate that our method outperforms the state-of-the-art academic and commercial model checkers on a set of standard hardware designs written in SystemVerilog.

Bisimulation Learning

We introduce a data-driven approach to computing finite bisimulations for state transition systems with very large, possibly infinite state space. Our novel technique computes stutter-insensitive bisimulations of deterministic systems, which we characterize as the problem of learning a state classifier together with a ranking function for each class. Our procedure learns a candidate state classifier and candidate ranking functions from a finite dataset of sample states; then, it checks whether these generalise to the entire state space using satisfiability modulo theory solving. Upon the affirmative answer, the procedure concludes that the classifier constitutes a valid stutter-insensitive bisimulation of the system. Upon a negative answer, the solver produces a counterexample state for which the classifier violates the claim, adds it to the dataset, and repeats learning and checking in a counterexample-guided inductive synthesis loop until a valid bisimulation is found. We demonstrate on a range of benchmarks from reactive verification and software model checking that our method yields faster verification results than alternative state-of-the-art tools in practice. Our method produces succinct abstractions that enable an effective verification of linear temporal logic without next operator, and are interpretable for system diagnostics.

On the Trade-off Between Efficiency and Precision of Neural Abstraction

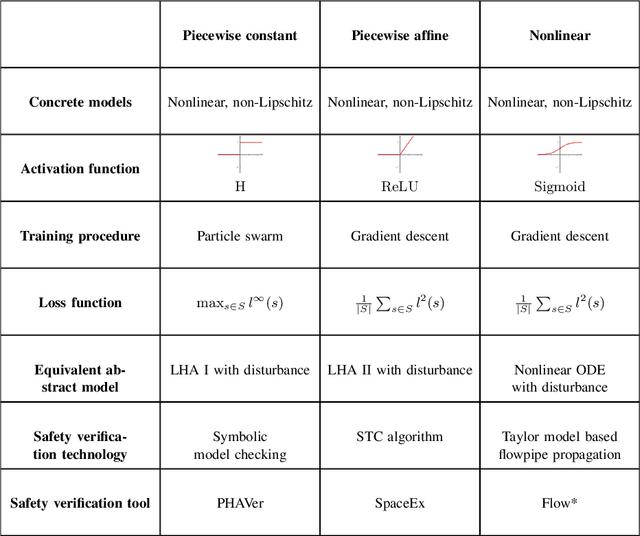
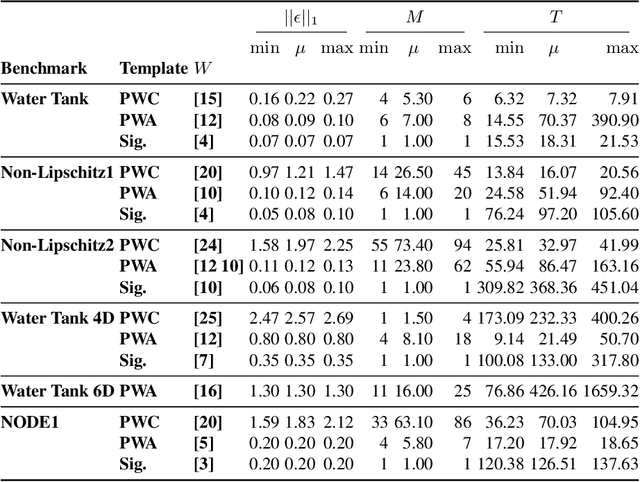
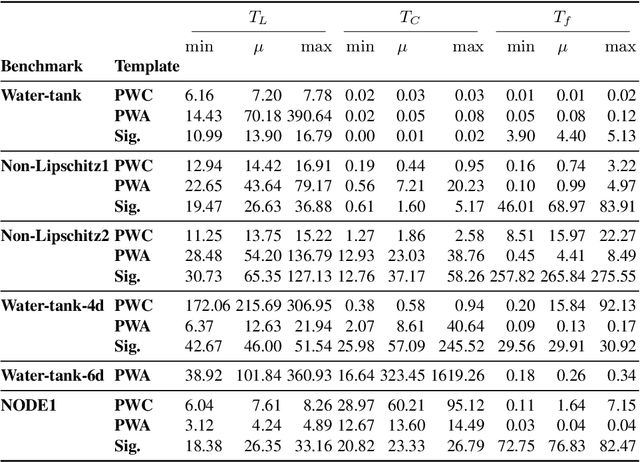
Neural abstractions have been recently introduced as formal approximations of complex, nonlinear dynamical models. They comprise a neural ODE and a certified upper bound on the error between the abstract neural network and the concrete dynamical model. So far neural abstractions have exclusively been obtained as neural networks consisting entirely of $ReLU$ activation functions, resulting in neural ODE models that have piecewise affine dynamics, and which can be equivalently interpreted as linear hybrid automata. In this work, we observe that the utility of an abstraction depends on its use: some scenarios might require coarse abstractions that are easier to analyse, whereas others might require more complex, refined abstractions. We therefore consider neural abstractions of alternative shapes, namely either piecewise constant or nonlinear non-polynomial (specifically, obtained via sigmoidal activations). We employ formal inductive synthesis procedures to generate neural abstractions that result in dynamical models with these semantics. Empirically, we demonstrate the trade-off that these different neural abstraction templates have vis-a-vis their precision and synthesis time, as well as the time required for their safety verification (done via reachability computation). We improve existing synthesis techniques to enable abstraction of higher-dimensional models, and additionally discuss the abstraction of complex neural ODEs to improve the efficiency of reachability analysis for these models.

Neural Abstractions

We present a novel method for the safety verification of nonlinear dynamical models that uses neural networks to represent abstractions of their dynamics. Neural networks have extensively been used before as approximators; in this work, we make a step further and use them for the first time as abstractions. For a given dynamical model, our method synthesises a neural network that overapproximates its dynamics by ensuring an arbitrarily tight, formally certified bound on the approximation error. For this purpose, we employ a counterexample-guided inductive synthesis procedure. We show that this produces a neural ODE with non-deterministic disturbances that constitutes a formal abstraction of the concrete model under analysis. This guarantees a fundamental property: if the abstract model is safe, i.e., free from any initialised trajectory that reaches an undesirable state, then the concrete model is also safe. By using neural ODEs with ReLU activation functions as abstractions, we cast the safety verification problem for nonlinear dynamical models into that of hybrid automata with affine dynamics, which we verify using SpaceEx. We demonstrate that our approach performs comparably to the mature tool Flow* on existing benchmark nonlinear models. We additionally demonstrate and that it is effective on models that do not exhibit local Lipschitz continuity, which are out of reach to the existing technologies.

Neural Termination Analysis

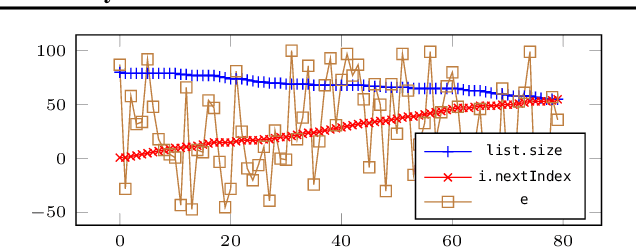
We introduce a novel approach to the automated termination analysis of computer programs: we train neural networks to act as ranking functions. Ranking functions map program states to values that are bounded from below and decrease as the program runs. The existence of a valid ranking function proves that the program terminates. While in the past ranking functions were usually constructed using static analysis, our method learns them from sampled executions. We train a neural network so that its output decreases along execution traces as a ranking function would; then, we use formal reasoning to verify whether it generalises to all possible executions. We present a custom loss function for learning lexicographic ranking functions and use satisfiability modulo theories for verification. Thanks to the ability of neural networks to generalise well, our method succeeds over a wide variety of programs. This includes programs that use data structures from standard libraries. We built a prototype analyser for Java bytecode and show the efficacy of our method over a standard dataset of benchmarks.

Shielding Atari Games with Bounded Prescience

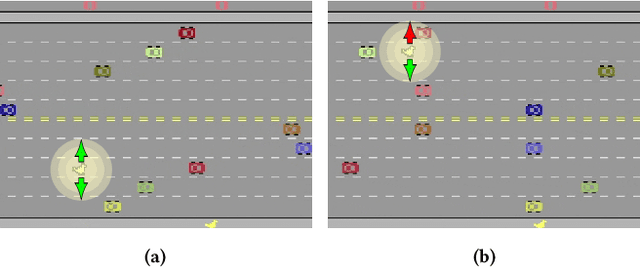
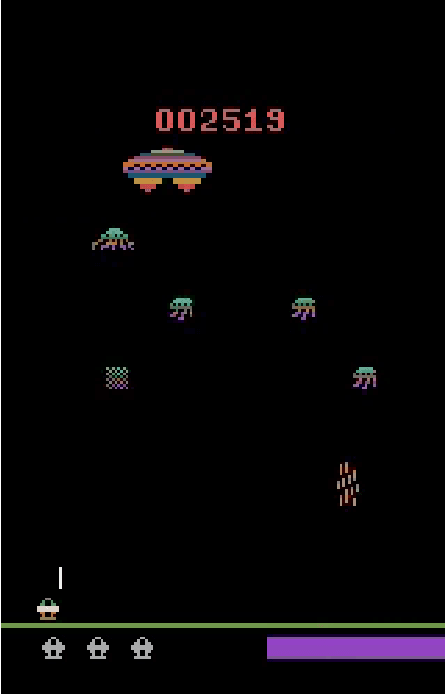
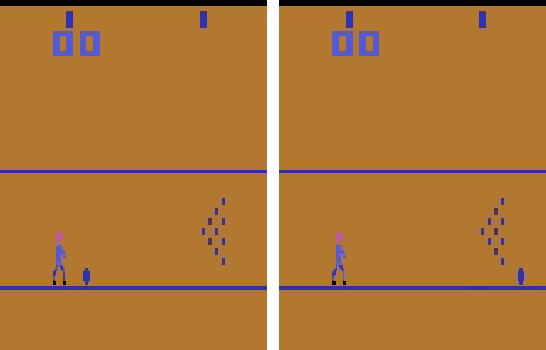
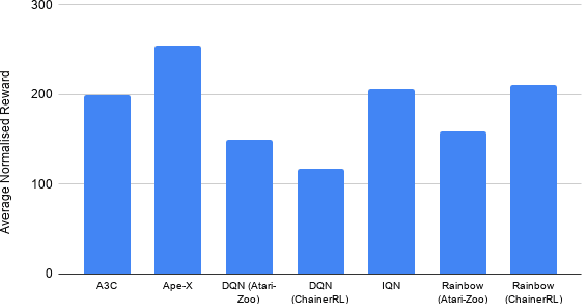
Deep reinforcement learning (DRL) is applied in safety-critical domains such as robotics and autonomous driving. It achieves superhuman abilities in many tasks, however whether DRL agents can be shown to act safely is an open problem. Atari games are a simple yet challenging exemplar for evaluating the safety of DRL agents and feature a diverse portfolio of game mechanics. The safety of neural agents has been studied before using methods that either require a model of the system dynamics or an abstraction; unfortunately, these are unsuitable to Atari games because their low-level dynamics are complex and hidden inside their emulator. We present the first exact method for analysing and ensuring the safety of DRL agents for Atari games. Our method only requires access to the emulator. First, we give a set of 43 properties that characterise "safe behaviour" for 30 games. Second, we develop a method for exploring all traces induced by an agent and a game and consider a variety of sources of game non-determinism. We observe that the best available DRL agents reliably satisfy only very few properties; several critical properties are violated by all agents. Finally, we propose a countermeasure that combines a bounded explicit-state exploration with shielding. We demonstrate that our method improves the safety of all agents over multiple properties.

Automated Formal Synthesis of Lyapunov Neural Networks

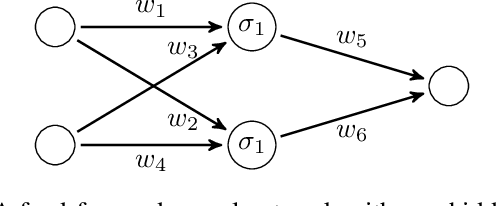
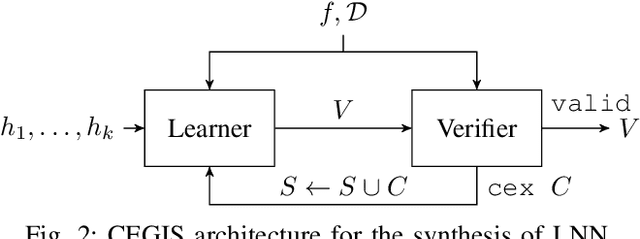
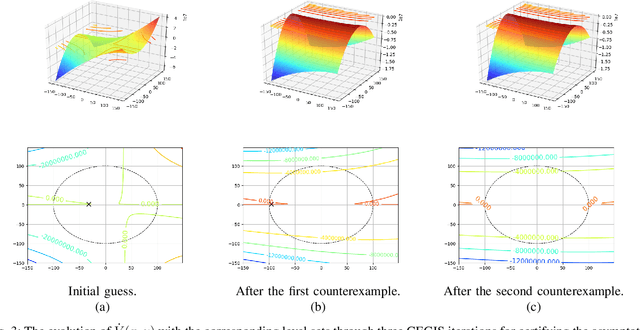
We propose an automated and sound technique to synthesize provably correct Lyapunov functions. We exploit a counterexample-guided approach composed of two parts: a learner provides candidate Lyapunov functions, and a verifier either guarantees the correctness of the candidate or offers counterexamples, which are used incrementally to further guide the synthesis of Lyapunov functions. Whilst the verifier employs a formal SMT solver, thus ensuring the overall soundness of the procedure, a neural network is used to learn and synthesize candidates over a domain of interest. Our approach flexibly supports neural networks of arbitrary size and depth, thus displaying interesting learning capabilities. In particular, we test our methodology over non-linear models that do not admit global polynomial Lyapunov functions, and compare the results against a cognate $\delta$-complete approach, and against an approach based on convex (SOS) optimization. The proposed technique outperforms these alternatives, synthesizing Lyapunov functions faster and over wider spatial domains.