Automated and Sound Synthesis of Lyapunov Functions with SMT Solvers

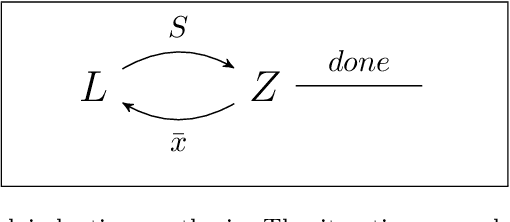
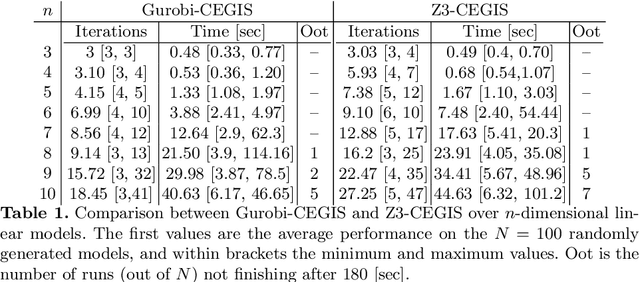
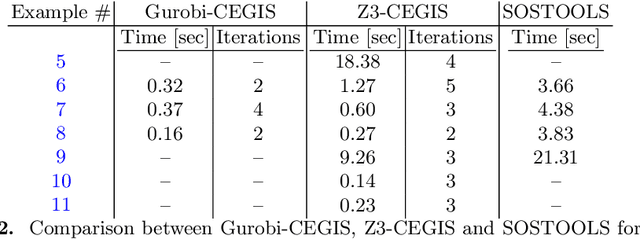
In this paper we employ SMT solvers to soundly synthesise Lyapunov functions that assert the stability of a given dynamical model. The search for a Lyapunov function is framed as the satisfiability of a second-order logical formula, asking whether there exists a function satisfying a desired specification (stability) for all possible initial conditions of the model. We synthesise Lyapunov functions for linear, non-linear (polynomial), and for parametric models. For non-linear models, the algorithm also determines a region of validity for the Lyapunov function. We exploit an inductive framework to synthesise Lyapunov functions, starting from parametric templates. The inductive framework comprises two elements: a learner proposes a Lyapunov function, and a verifier checks its validity - its lack is expressed via a counterexample (a point over the state space), for further use by the learner. Whilst the verifier uses the SMT solver Z3, thus ensuring the overall soundness of the procedure, we examine two alternatives for the learner: a numerical approach based on the optimisation tool Gurobi, and a sound approach based again on Z3. The overall technique is evaluated over a broad set of benchmarks, which shows that this methodology not only scales to 10-dimensional models within reasonable computational time, but also offers a novel soundness proof for the generated Lyapunov functions and their domains of validity.

Automated Formal Synthesis of Neural Barrier Certificates for Dynamical Models

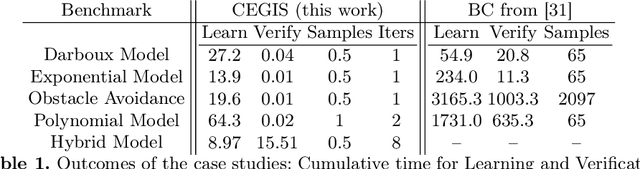
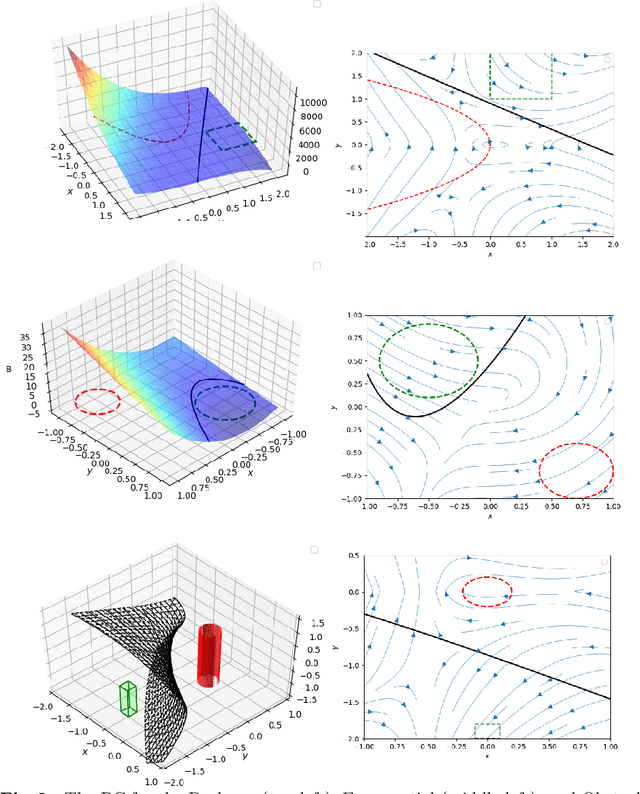
We introduce an automated, formal, counterexample-based approach to synthesise Barrier Certificates (BC) for the safety verification of continuous and hybrid dynamical models. The approach is underpinned by an inductive framework: this is structured as a sequential loop between a learner, which manipulates a candidate BC as a neural network, and a sound verifier, which either certifies through algorithmic proofs the candidate's validity or generates counter-examples to further guide the learner. We compare the approach against state-of-the-art techniques, over polynomial and non-polynomial dynamical models: the outcomes show that we can synthesise sound BCs up to two orders of magnitude faster, with in particular a stark speedup on the verification engine (up to five orders less), whilst needing a far smaller data set (up to three orders less) for the learning part. Beyond the state of the art, we further challenge the (verification side of the) approach on a hybrid dynamical model.

Automated Formal Synthesis of Lyapunov Neural Networks

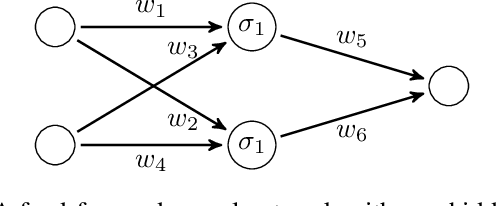
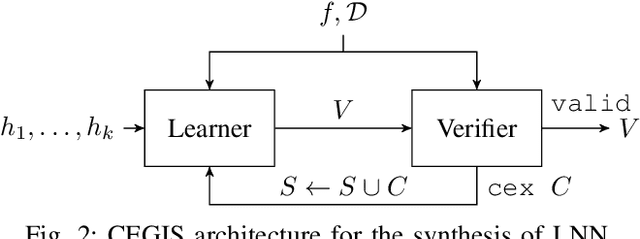
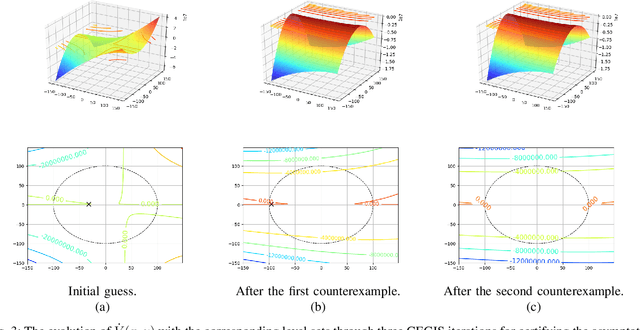
We propose an automated and sound technique to synthesize provably correct Lyapunov functions. We exploit a counterexample-guided approach composed of two parts: a learner provides candidate Lyapunov functions, and a verifier either guarantees the correctness of the candidate or offers counterexamples, which are used incrementally to further guide the synthesis of Lyapunov functions. Whilst the verifier employs a formal SMT solver, thus ensuring the overall soundness of the procedure, a neural network is used to learn and synthesize candidates over a domain of interest. Our approach flexibly supports neural networks of arbitrary size and depth, thus displaying interesting learning capabilities. In particular, we test our methodology over non-linear models that do not admit global polynomial Lyapunov functions, and compare the results against a cognate $\delta$-complete approach, and against an approach based on convex (SOS) optimization. The proposed technique outperforms these alternatives, synthesizing Lyapunov functions faster and over wider spatial domains.