Certified Approximate Reachability (CARe): Formal Error Bounds on Deep Learning of Reachable Sets

Recent approaches to leveraging deep learning for computing reachable sets of continuous-time dynamical systems have gained popularity over traditional level-set methods, as they overcome the curse of dimensionality. However, as with level-set methods, considerable care needs to be taken in limiting approximation errors, particularly since no guarantees are provided during training on the accuracy of the learned reachable set. To address this limitation, we introduce an epsilon-approximate Hamilton-Jacobi Partial Differential Equation (HJ-PDE), which establishes a relationship between training loss and accuracy of the true reachable set. To formally certify this approximation, we leverage Satisfiability Modulo Theories (SMT) solvers to bound the residual error of the HJ-based loss function across the domain of interest. Leveraging Counter Example Guided Inductive Synthesis (CEGIS), we close the loop around learning and verification, by fine-tuning the neural network on counterexamples found by the SMT solver, thus improving the accuracy of the learned reachable set. To the best of our knowledge, Certified Approximate Reachability (CARe) is the first approach to provide soundness guarantees on learned reachable sets of continuous dynamical systems.

Finite sample learning of moving targets

We consider a moving target that we seek to learn from samples. Our results extend randomized techniques developed in control and optimization for a constant target to the case where the target is changing. We derive a novel bound on the number of samples that are required to construct a probably approximately correct (PAC) estimate of the target. Furthermore, when the moving target is a convex polytope, we provide a constructive method of generating the PAC estimate using a mixed integer linear program (MILP). The proposed method is demonstrated on an application to autonomous emergency braking.

Verification of safety critical control policies using kernel methods

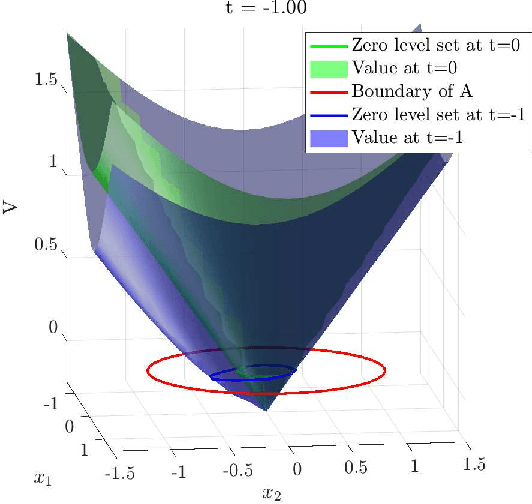
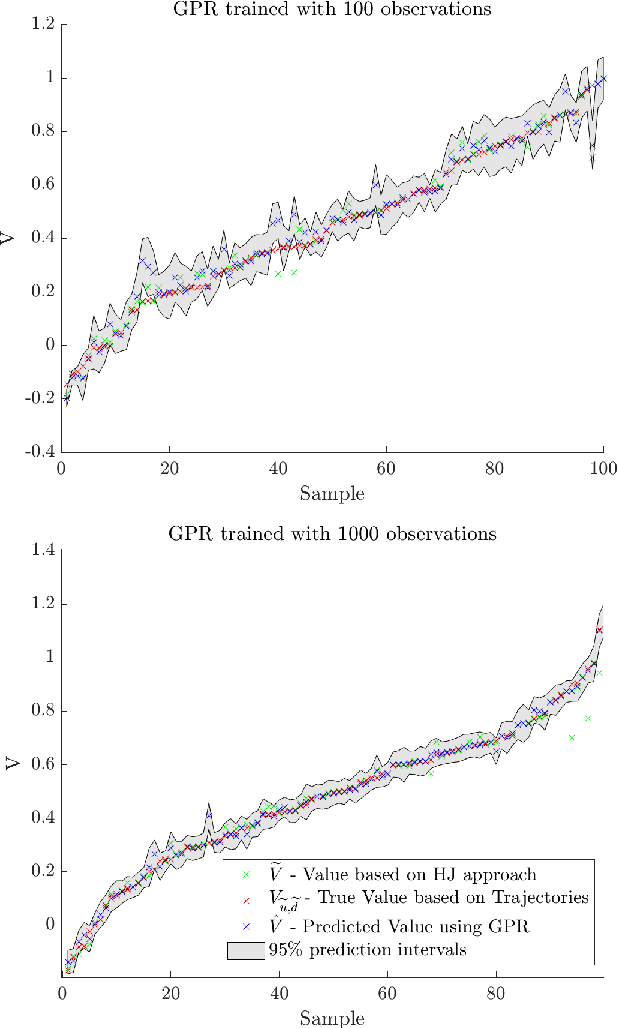
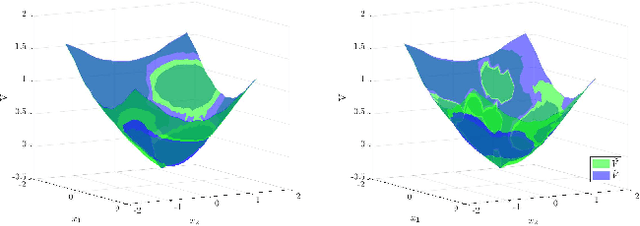
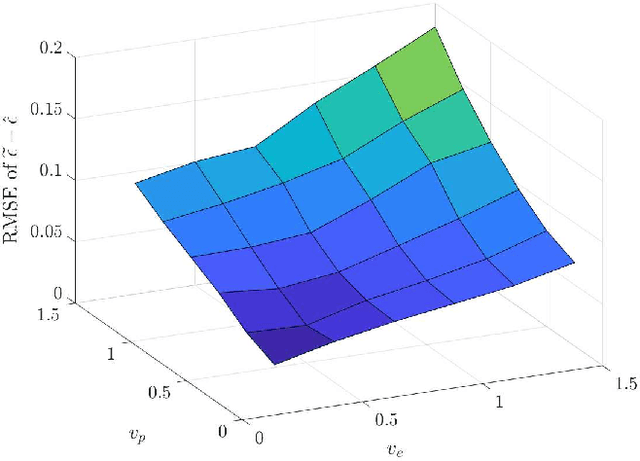
Hamilton-Jacobi reachability methods for safety-critical control have been well studied, but the safety guarantees derived rely on the accuracy of the numerical computation. Thus, it is crucial to understand and account for any inaccuracies that occur due to uncertainty in the underlying dynamics and environment as well as the induced numerical errors. To this end, we propose a framework for modeling the error of the value function inherent in Hamilton-Jacobi reachability using a Gaussian process. The derived safety controller can be used in conjuncture with arbitrary controllers to provide a safe hybrid control law. The marginal likelihood of the Gaussian process then provides a confidence metric used to determine switches between a least restrictive controller and a safety controller. We test both the prediction as well as the correction capabilities of the presented method in a classical pursuit-evasion example.