Scalable Formal Verification via Autoencoder Latent Space Abstraction

Finite Abstraction methods provide a powerful formal framework for proving that systems satisfy their specifications. However, these techniques face scalability challenges for high-dimensional systems, as they rely on state-space discretization which grows exponentially with dimension. Learning-based approaches to dimensionality reduction, utilizing neural networks and autoencoders, have shown great potential to alleviate this problem. However, ensuring the correctness of the resulting verification results remains an open question. In this work, we provide a formal approach to reduce the dimensionality of systems via convex autoencoders and learn the dynamics in the latent space through a kernel-based method. We then construct a finite abstraction from the learned model in the latent space and guarantee that the abstraction contains the true behaviors of the original system. We show that the verification results in the latent space can be mapped back to the original system. Finally, we demonstrate the effectiveness of our approach on multiple systems, including a 26D system controlled by a neural network, showing significant scalability improvements without loss of rigor.

Scalable Verification of Neural Control Barrier Functions Using Linear Bound Propagation

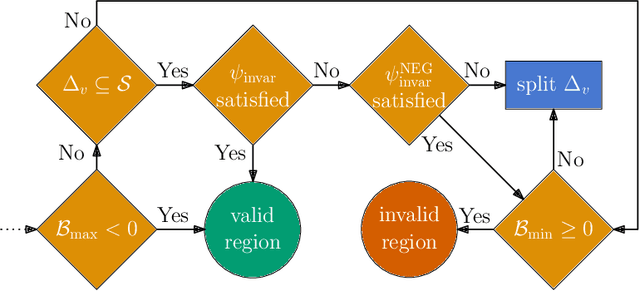
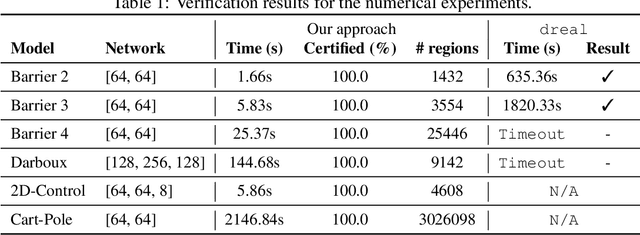
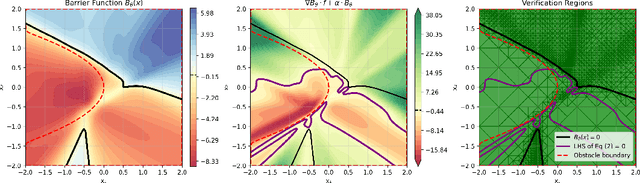
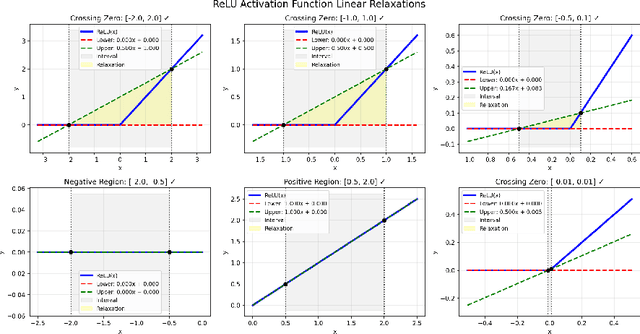
Control barrier functions (CBFs) are a popular tool for safety certification of nonlinear dynamical control systems. Recently, CBFs represented as neural networks have shown great promise due to their expressiveness and applicability to a broad class of dynamics and safety constraints. However, verifying that a trained neural network is indeed a valid CBF is a computational bottleneck that limits the size of the networks that can be used. To overcome this limitation, we present a novel framework for verifying neural CBFs based on piecewise linear upper and lower bounds on the conditions required for a neural network to be a CBF. Our approach is rooted in linear bound propagation (LBP) for neural networks, which we extend to compute bounds on the gradients of the network. Combined with McCormick relaxation, we derive linear upper and lower bounds on the CBF conditions, thereby eliminating the need for computationally expensive verification procedures. Our approach applies to arbitrary control-affine systems and a broad range of nonlinear activation functions. To reduce conservatism, we develop a parallelizable refinement strategy that adaptively refines the regions over which these bounds are computed. Our approach scales to larger neural networks than state-of-the-art verification procedures for CBFs, as demonstrated by our numerical experiments.

Certified Neural Approximations of Nonlinear Dynamics

Neural networks hold great potential to act as approximate models of nonlinear dynamical systems, with the resulting neural approximations enabling verification and control of such systems. However, in safety-critical contexts, the use of neural approximations requires formal bounds on their closeness to the underlying system. To address this fundamental challenge, we propose a novel, adaptive, and parallelizable verification method based on certified first-order models. Our approach provides formal error bounds on the neural approximations of dynamical systems, allowing them to be safely employed as surrogates by interpreting the error bound as bounded disturbances acting on the approximated dynamics. We demonstrate the effectiveness and scalability of our method on a range of established benchmarks from the literature, showing that it outperforms the state-of-the-art. Furthermore, we highlight the flexibility of our framework by applying it to two novel scenarios not previously explored in this context: neural network compression and an autoencoder-based deep learning architecture for learning Koopman operators, both yielding compelling results.

Error Bounds for Deep Learning-based Uncertainty Propagation in SDEs

Stochastic differential equations are commonly used to describe the evolution of stochastic processes. The uncertainty of such processes is best represented by the probability density function (PDF), whose evolution is governed by the Fokker-Planck partial differential equation (FP-PDE). However, it is generally infeasible to solve the FP-PDE in closed form. In this work, we show that physics-informed neural networks (PINNs) can be trained to approximate the solution PDF using existing methods. The main contribution is the analysis of the approximation error: we develop a theory to construct an arbitrary tight error bound with PINNs. In addition, we derive a practical error bound that can be efficiently constructed with existing training methods. Finally, we explain that this error-bound theory generalizes to approximate solutions of other linear PDEs. Several numerical experiments are conducted to demonstrate and validate the proposed methods.

Error Bounds For Gaussian Process Regression Under Bounded Support Noise With Applications To Safety Certification

Gaussian Process Regression (GPR) is a powerful and elegant method for learning complex functions from noisy data with a wide range of applications, including in safety-critical domains. Such applications have two key features: (i) they require rigorous error quantification, and (ii) the noise is often bounded and non-Gaussian due to, e.g., physical constraints. While error bounds for applying GPR in the presence of non-Gaussian noise exist, they tend to be overly restrictive and conservative in practice. In this paper, we provide novel error bounds for GPR under bounded support noise. Specifically, by relying on concentration inequalities and assuming that the latent function has low complexity in the reproducing kernel Hilbert space (RKHS) corresponding to the GP kernel, we derive both probabilistic and deterministic bounds on the error of the GPR. We show that these errors are substantially tighter than existing state-of-the-art bounds and are particularly well-suited for GPR with neural network kernels, i.e., Deep Kernel Learning (DKL). Furthermore, motivated by applications in safety-critical domains, we illustrate how these bounds can be combined with stochastic barrier functions to successfully quantify the safety probability of an unknown dynamical system from finite data. We validate the efficacy of our approach through several benchmarks and comparisons against existing bounds. The results show that our bounds are consistently smaller, and that DKLs can produce error bounds tighter than sample noise, significantly improving the safety probability of control systems.

Finite Neural Networks as Mixtures of Gaussian Processes: From Provable Error Bounds to Prior Selection

Infinitely wide or deep neural networks (NNs) with independent and identically distributed (i.i.d.) parameters have been shown to be equivalent to Gaussian processes. Because of the favorable properties of Gaussian processes, this equivalence is commonly employed to analyze neural networks and has led to various breakthroughs over the years. However, neural networks and Gaussian processes are equivalent only in the limit; in the finite case there are currently no methods available to approximate a trained neural network with a Gaussian model with bounds on the approximation error. In this work, we present an algorithmic framework to approximate a neural network of finite width and depth, and with not necessarily i.i.d. parameters, with a mixture of Gaussian processes with error bounds on the approximation error. In particular, we consider the Wasserstein distance to quantify the closeness between probabilistic models and, by relying on tools from optimal transport and Gaussian processes, we iteratively approximate the output distribution of each layer of the neural network as a mixture of Gaussian processes. Crucially, for any NN and $\epsilon >0$ our approach is able to return a mixture of Gaussian processes that is $\epsilon$-close to the NN at a finite set of input points. Furthermore, we rely on the differentiability of the resulting error bound to show how our approach can be employed to tune the parameters of a NN to mimic the functional behavior of a given Gaussian process, e.g., for prior selection in the context of Bayesian inference. We empirically investigate the effectiveness of our results on both regression and classification problems with various neural network architectures. Our experiments highlight how our results can represent an important step towards understanding neural network predictions and formally quantifying their uncertainty.

Data-Driven Permissible Safe Control with Barrier Certificates

This paper introduces a method of identifying a maximal set of safe strategies from data for stochastic systems with unknown dynamics using barrier certificates. The first step is learning the dynamics of the system via Gaussian process (GP) regression and obtaining probabilistic errors for this estimate. Then, we develop an algorithm for constructing piecewise stochastic barrier functions to find a maximal permissible strategy set using the learned GP model, which is based on sequentially pruning the worst controls until a maximal set is identified. The permissible strategies are guaranteed to maintain probabilistic safety for the true system. This is especially important for learning-enabled systems, because a rich strategy space enables additional data collection and complex behaviors while remaining safe. Case studies on linear and nonlinear systems demonstrate that increasing the size of the dataset for learning the system grows the permissible strategy set.

Piecewise Stochastic Barrier Functions

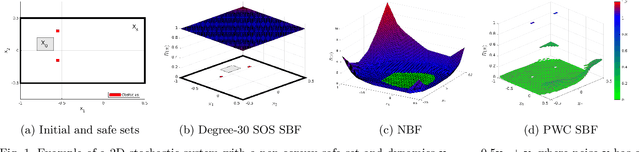
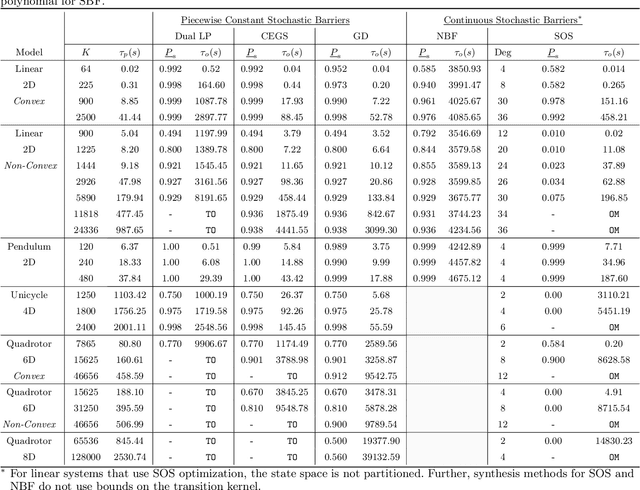
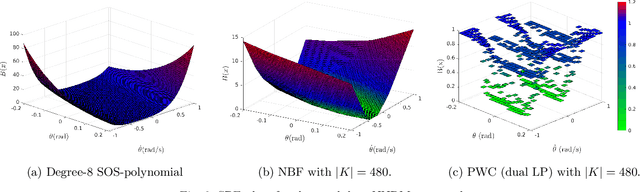
This paper presents a novel stochastic barrier function (SBF) framework for safety analysis of stochastic systems based on piecewise (PW) functions. We first outline a general formulation of PW-SBFs. Then, we focus on PW-Constant (PWC) SBFs and show how their simplicity yields computational advantages for general stochastic systems. Specifically, we prove that synthesis of PWC-SBFs reduces to a minimax optimization problem. Then, we introduce three efficient algorithms to solve this problem, each offering distinct advantages and disadvantages. The first algorithm is based on dual linear programming (LP), which provides an exact solution to the minimax optimization problem. The second is a more scalable algorithm based on iterative counter-example guided synthesis, which involves solving two smaller LPs. The third algorithm solves the minimax problem using gradient descent, which admits even better scalability. We provide an extensive evaluation of these methods on various case studies, including neural network dynamic models, nonlinear switched systems, and high-dimensional linear systems. Our benchmarks demonstrate that PWC-SBFs outperform state-of-the-art methods, namely sum-of-squares and neural barrier functions, and can scale to eight dimensional systems.

Probabilistic Reach-Avoid for Bayesian Neural Networks

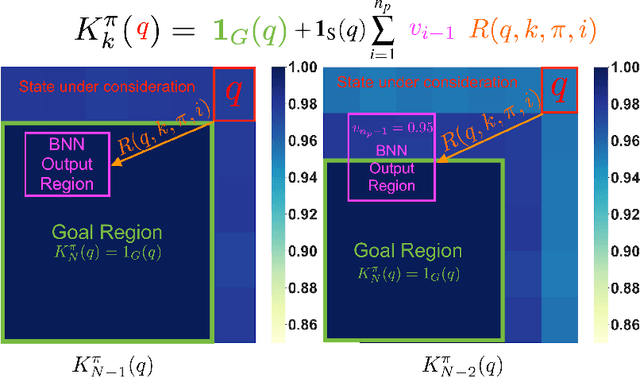
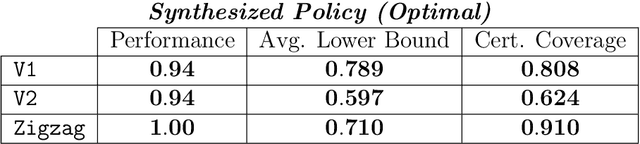
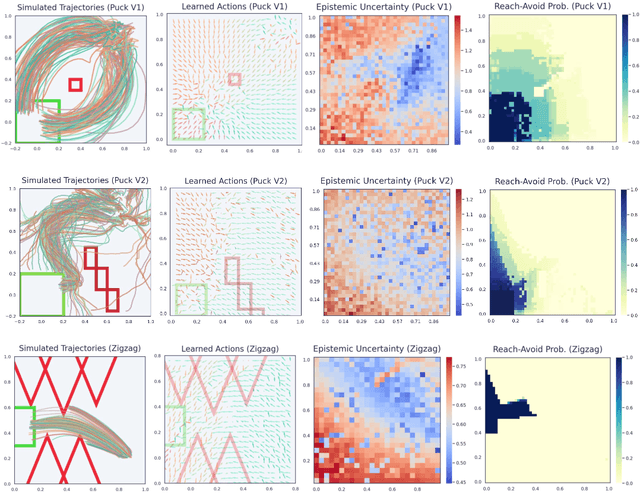
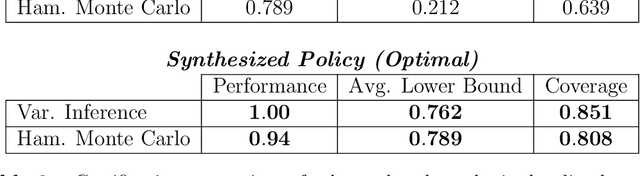
Model-based reinforcement learning seeks to simultaneously learn the dynamics of an unknown stochastic environment and synthesise an optimal policy for acting in it. Ensuring the safety and robustness of sequential decisions made through a policy in such an environment is a key challenge for policies intended for safety-critical scenarios. In this work, we investigate two complementary problems: first, computing reach-avoid probabilities for iterative predictions made with dynamical models, with dynamics described by Bayesian neural network (BNN); second, synthesising control policies that are optimal with respect to a given reach-avoid specification (reaching a "target" state, while avoiding a set of "unsafe" states) and a learned BNN model. Our solution leverages interval propagation and backward recursion techniques to compute lower bounds for the probability that a policy's sequence of actions leads to satisfying the reach-avoid specification. Such computed lower bounds provide safety certification for the given policy and BNN model. We then introduce control synthesis algorithms to derive policies maximizing said lower bounds on the safety probability. We demonstrate the effectiveness of our method on a series of control benchmarks characterized by learned BNN dynamics models. On our most challenging benchmark, compared to purely data-driven policies the optimal synthesis algorithm is able to provide more than a four-fold increase in the number of certifiable states and more than a three-fold increase in the average guaranteed reach-avoid probability.

Promises of Deep Kernel Learning for Control Synthesis

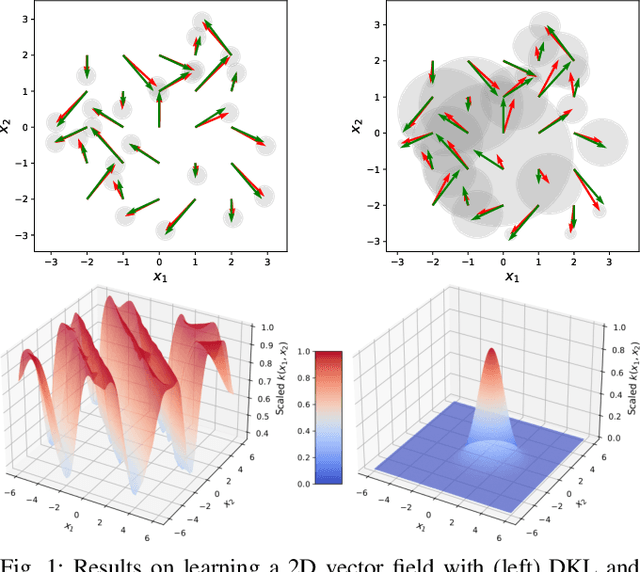
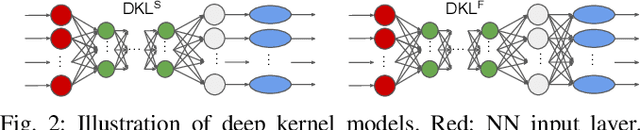
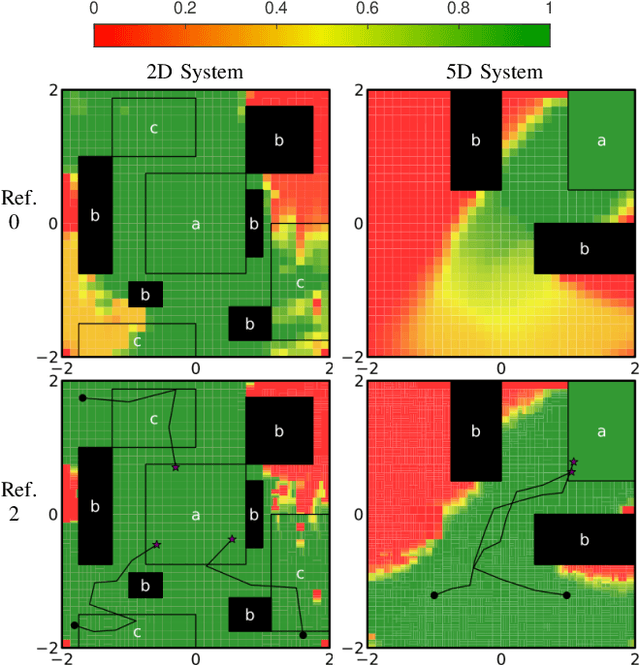
Deep Kernel Learning (DKL) combines the representational power of neural networks with the uncertainty quantification of Gaussian Processes. Hence, it is potentially a promising tool to learn and control complex dynamical systems. In this work, we develop a scalable abstraction-based framework that enables the use of DKL for control synthesis of stochastic dynamical systems against complex specifications. Specifically, we consider temporal logic specifications and create an end-to-end framework that uses DKL to learn an unknown system from data and formally abstracts the DKL model into an Interval Markov Decision Process (IMDP) to perform control synthesis with correctness guarantees. Furthermore, we identify a deep architecture that enables accurate learning and efficient abstraction computation. The effectiveness of our approach is illustrated on various benchmarks, including a 5-D nonlinear stochastic system, showing how control synthesis with DKL can substantially outperform state-of-the-art competitive methods.