Adversarial Robustness Certification for Bayesian Neural Networks
Paper and Code
Jun 23, 2023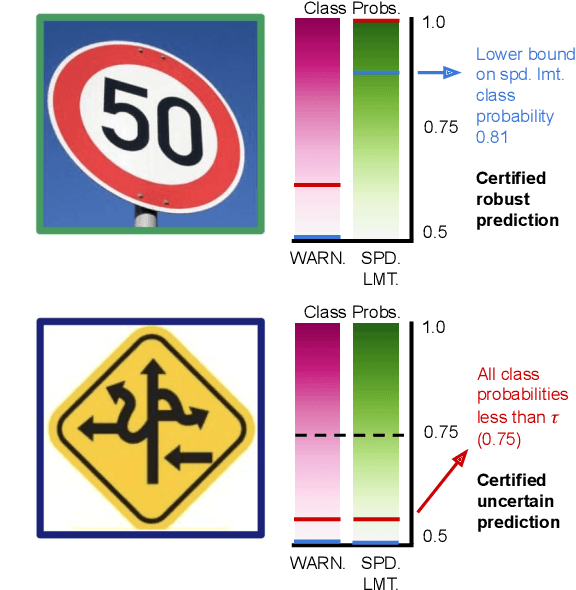
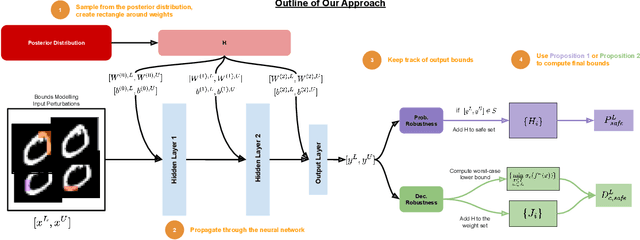
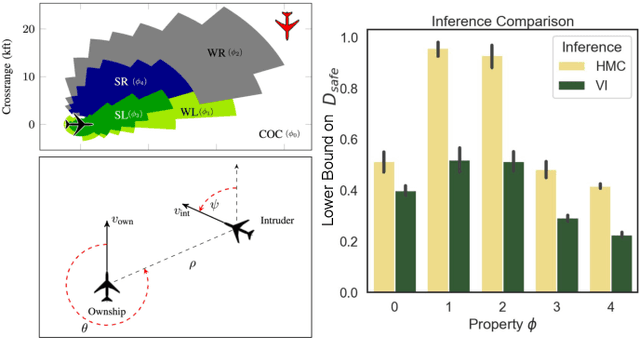
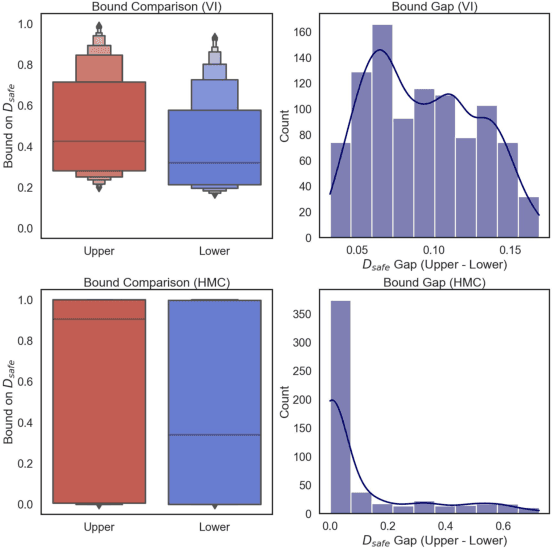
We study the problem of certifying the robustness of Bayesian neural networks (BNNs) to adversarial input perturbations. Given a compact set of input points $T \subseteq \mathbb{R}^m$ and a set of output points $S \subseteq \mathbb{R}^n$, we define two notions of robustness for BNNs in an adversarial setting: probabilistic robustness and decision robustness. Probabilistic robustness is the probability that for all points in $T$ the output of a BNN sampled from the posterior is in $S$. On the other hand, decision robustness considers the optimal decision of a BNN and checks if for all points in $T$ the optimal decision of the BNN for a given loss function lies within the output set $S$. Although exact computation of these robustness properties is challenging due to the probabilistic and non-convex nature of BNNs, we present a unified computational framework for efficiently and formally bounding them. Our approach is based on weight interval sampling, integration, and bound propagation techniques, and can be applied to BNNs with a large number of parameters, and independently of the (approximate) inference method employed to train the BNN. We evaluate the effectiveness of our methods on various regression and classification tasks, including an industrial regression benchmark, MNIST, traffic sign recognition, and airborne collision avoidance, and demonstrate that our approach enables certification of robustness and uncertainty of BNN predictions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge