Marta Kwiatkowska
University of Oxford
About Time: Model-free Reinforcement Learning with Timed Reward Machines
Dec 19, 2025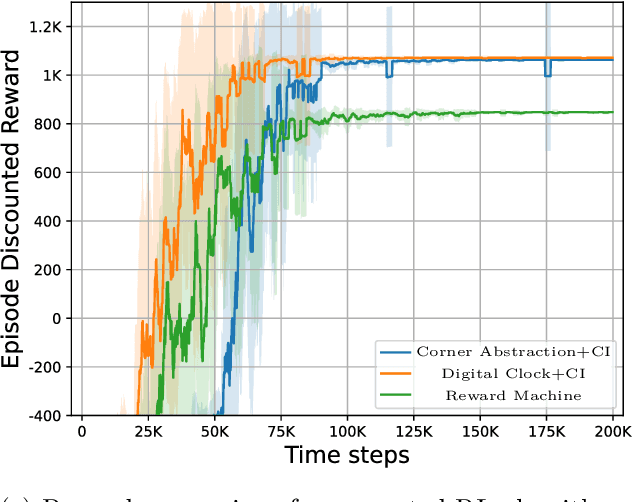
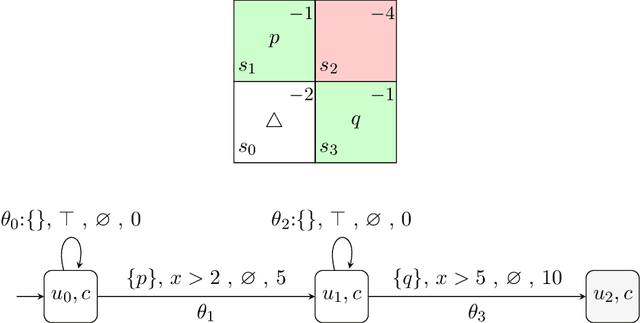

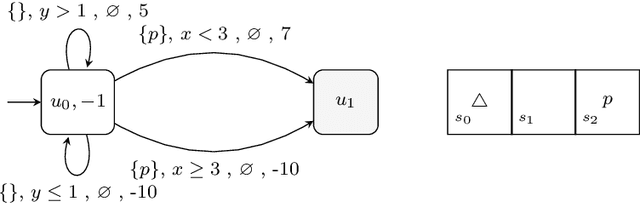
Abstract:Reward specification plays a central role in reinforcement learning (RL), guiding the agent's behavior. To express non-Markovian rewards, formalisms such as reward machines have been introduced to capture dependencies on histories. However, traditional reward machines lack the ability to model precise timing constraints, limiting their use in time-sensitive applications. In this paper, we propose timed reward machines (TRMs), which are an extension of reward machines that incorporate timing constraints into the reward structure. TRMs enable more expressive specifications with tunable reward logic, for example, imposing costs for delays and granting rewards for timely actions. We study model-free RL frameworks (i.e., tabular Q-learning) for learning optimal policies with TRMs under digital and real-time semantics. Our algorithms integrate the TRM into learning via abstractions of timed automata, and employ counterfactual-imagining heuristics that exploit the structure of the TRM to improve the search. Experimentally, we demonstrate that our algorithm learns policies that achieve high rewards while satisfying the timing constraints specified by the TRM on popular RL benchmarks. Moreover, we conduct comparative studies of performance under different TRM semantics, along with ablations that highlight the benefits of counterfactual-imagining.
PyVeritas: On Verifying Python via LLM-Based Transpilation and Bounded Model Checking for C
Aug 11, 2025Abstract:Python has become the dominant language for general-purpose programming, yet it lacks robust tools for formal verification. In contrast, programmers working in languages such as C benefit from mature model checkers, for example CBMC, which enable exhaustive symbolic reasoning and fault localisation. The inherent complexity of Python, coupled with the verbosity and low-level nature of existing transpilers (e.g., Cython), have historically limited the applicability of formal verification to Python programs. In this paper, we propose PyVeritas, a novel framework that leverages Large Language Models (LLMs) for high-level transpilation from Python to C, followed by bounded model checking and MaxSAT-based fault localisation in the generated C code. PyVeritas enables verification and bug localisation for Python code using existing model checking tools for C. Our empirical evaluation on two Python benchmarks demonstrates that LLM-based transpilation can achieve a high degree of accuracy, up to 80--90% for some LLMs, enabling effective development environment that supports assertion-based verification and interpretable fault diagnosis for small yet non-trivial Python programs.
Double Machine Learning for Conditional Moment Restrictions: IV regression, Proximal Causal Learning and Beyond
Jun 17, 2025Abstract:Solving conditional moment restrictions (CMRs) is a key problem considered in statistics, causal inference, and econometrics, where the aim is to solve for a function of interest that satisfies some conditional moment equalities. Specifically, many techniques for causal inference, such as instrumental variable (IV) regression and proximal causal learning (PCL), are CMR problems. Most CMR estimators use a two-stage approach, where the first-stage estimation is directly plugged into the second stage to estimate the function of interest. However, naively plugging in the first-stage estimator can cause heavy bias in the second stage. This is particularly the case for recently proposed CMR estimators that use deep neural network (DNN) estimators for both stages, where regularisation and overfitting bias is present. We propose DML-CMR, a two-stage CMR estimator that provides an unbiased estimate with fast convergence rate guarantees. We derive a novel learning objective to reduce bias and develop the DML-CMR algorithm following the double/debiased machine learning (DML) framework. We show that our DML-CMR estimator can achieve the minimax optimal convergence rate of $O(N^{-1/2})$ under parameterisation and mild regularity conditions, where $N$ is the sample size. We apply DML-CMR to a range of problems using DNN estimators, including IV regression and proximal causal learning on real-world datasets, demonstrating state-of-the-art performance against existing CMR estimators and algorithms tailored to those problems.
Efficient Preimage Approximation for Neural Network Certification
May 28, 2025Abstract:The growing reliance on artificial intelligence in safety- and security-critical applications demands effective neural network certification. A challenging real-world use case is certification against ``patch attacks'', where adversarial patches or lighting conditions obscure parts of images, for example traffic signs. One approach to certification, which also gives quantitative coverage estimates, utilizes preimages of neural networks, i.e., the set of inputs that lead to a specified output. However, these preimage approximation methods, including the state-of-the-art PREMAP algorithm, struggle with scalability. This paper presents novel algorithmic improvements to PREMAP involving tighter bounds, adaptive Monte Carlo sampling, and improved branching heuristics. We demonstrate efficiency improvements of at least an order of magnitude on reinforcement learning control benchmarks, and show that our method scales to convolutional neural networks that were previously infeasible. Our results demonstrate the potential of preimage approximation methodology for reliability and robustness certification.
Learning Probabilistic Temporal Logic Specifications for Stochastic Systems
May 17, 2025Abstract:There has been substantial progress in the inference of formal behavioural specifications from sample trajectories, for example, using Linear Temporal Logic (LTL). However, these techniques cannot handle specifications that correctly characterise systems with stochastic behaviour, which occur commonly in reinforcement learning and formal verification. We consider the passive learning problem of inferring a Boolean combination of probabilistic LTL (PLTL) formulas from a set of Markov chains, classified as either positive or negative. We propose a novel learning algorithm that infers concise PLTL specifications, leveraging grammar-based enumeration, search heuristics, probabilistic model checking and Boolean set-cover procedures. We demonstrate the effectiveness of our algorithm in two use cases: learning from policies induced by RL algorithms and learning from variants of a probabilistic model. In both cases, our method automatically and efficiently extracts PLTL specifications that succinctly characterise the temporal differences between the policies or model variants.
Are Large Language Models Robust in Understanding Code Against Semantics-Preserving Mutations?
May 15, 2025Abstract:Understanding the reasoning and robustness of Large Language Models (LLMs) is critical for their reliable use in programming tasks. While recent studies have assessed LLMs' ability to predict program outputs, most focus solely on the accuracy of those predictions, without evaluating the reasoning behind them. Moreover, it has been observed on mathematical reasoning tasks that LLMs can arrive at correct answers through flawed logic, raising concerns about similar issues in code understanding. In this work, we evaluate whether state-of-the-art LLMs with up to 8B parameters can reason about Python programs or are simply guessing. We apply five semantics-preserving code mutations: renaming variables, mirroring comparison expressions, swapping if-else branches, converting for loops to while, and loop unrolling. These mutations maintain program semantics while altering its syntax. We evaluated six LLMs and performed a human expert analysis using LiveCodeBench to assess whether the correct predictions are based on sound reasoning. We also evaluated prediction stability across different code mutations on LiveCodeBench and CruxEval. Our findings show that some LLMs, such as Llama3.2, produce correct predictions based on flawed reasoning in up to 61% of cases. Furthermore, LLMs often change predictions in response to our code mutations, indicating limited robustness in their semantic understanding.
Strategyproof Reinforcement Learning from Human Feedback
Mar 12, 2025Abstract:We study Reinforcement Learning from Human Feedback (RLHF), where multiple individuals with diverse preferences provide feedback strategically to sway the final policy in their favor. We show that existing RLHF methods are not strategyproof, which can result in learning a substantially misaligned policy even when only one out of $k$ individuals reports their preferences strategically. In turn, we also find that any strategyproof RLHF algorithm must perform $k$-times worse than the optimal policy, highlighting an inherent trade-off between incentive alignment and policy alignment. We then propose a pessimistic median algorithm that, under appropriate coverage assumptions, is approximately strategyproof and converges to the optimal policy as the number of individuals and samples increases.
Planning with Linear Temporal Logic Specifications: Handling Quantifiable and Unquantifiable Uncertainty
Feb 26, 2025Abstract:This work studies the planning problem for robotic systems under both quantifiable and unquantifiable uncertainty. The objective is to enable the robotic systems to optimally fulfill high-level tasks specified by Linear Temporal Logic (LTL) formulas. To capture both types of uncertainty in a unified modelling framework, we utilise Markov Decision Processes with Set-valued Transitions (MDPSTs). We introduce a novel solution technique for the optimal robust strategy synthesis of MDPSTs with LTL specifications. To improve efficiency, our work leverages limit-deterministic B\"uchi automata (LDBAs) as the automaton representation for LTL to take advantage of their efficient constructions. To tackle the inherent nondeterminism in MDPSTs, which presents a significant challenge for reducing the LTL planning problem to a reachability problem, we introduce the concept of a Winning Region (WR) for MDPSTs. Additionally, we propose an algorithm for computing the WR over the product of the MDPST and the LDBA. Finally, a robust value iteration algorithm is invoked to solve the reachability problem. We validate the effectiveness of our approach through a case study involving a mobile robot operating in the hexagonal world, demonstrating promising efficiency gains.
A Unifying Framework for Causal Imitation Learning with Hidden Confounders
Feb 11, 2025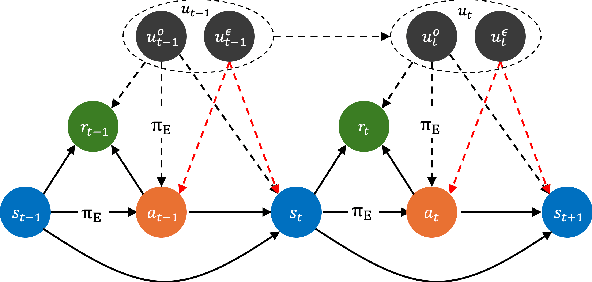

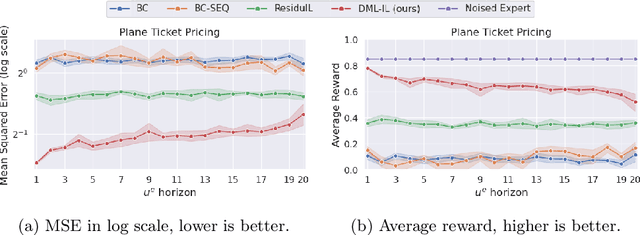
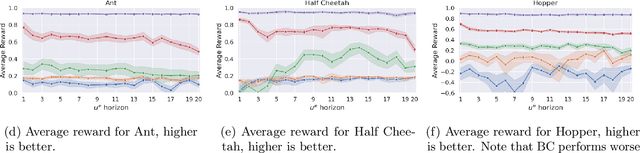
Abstract:We propose a general and unifying framework for causal Imitation Learning (IL) with hidden confounders that subsumes several existing confounded IL settings from the literature. Our framework accounts for two types of hidden confounders: (a) those observed by the expert, which thus influence the expert's policy, and (b) confounding noise hidden to both the expert and the IL algorithm. For additional flexibility, we also introduce a confounding noise horizon and time-varying expert-observable hidden variables. We show that causal IL in our framework can be reduced to a set of Conditional Moment Restrictions (CMRs) by leveraging trajectory histories as instruments to learn a history-dependent policy. We propose DML-IL, a novel algorithm that uses instrumental variable regression to solve these CMRs and learn a policy. We provide a bound on the imitation gap for DML-IL, which recovers prior results as special cases. Empirical evaluation on a toy environment with continues state-action spaces and multiple Mujoco tasks demonstrate that DML-IL outperforms state-of-the-art causal IL algorithms.
BiCert: A Bilinear Mixed Integer Programming Formulation for Precise Certified Bounds Against Data Poisoning Attacks
Dec 13, 2024Abstract:Data poisoning attacks pose one of the biggest threats to modern AI systems, necessitating robust defenses. While extensive efforts have been made to develop empirical defenses, attackers continue to evolve, creating sophisticated methods to circumvent these measures. To address this, we must move beyond empirical defenses and establish provable certification methods that guarantee robustness. This paper introduces a novel certification approach, BiCert, using Bilinear Mixed Integer Programming (BMIP) to compute sound deterministic bounds that provide such provable robustness. Using BMIP, we compute the reachable set of parameters that could result from training with potentially manipulated data. A key element to make this computation feasible is to relax the reachable parameter set to a convex set between training iterations. At test time, this parameter set allows us to predict all possible outcomes, guaranteeing robustness. BiCert is more precise than previous methods, which rely solely on interval and polyhedral bounds. Crucially, our approach overcomes the fundamental limitation of prior approaches where parameter bounds could only grow, often uncontrollably. We show that BiCert's tighter bounds eliminate a key source of divergence issues, resulting in more stable training and higher certified accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge