Strategyproof Reinforcement Learning from Human Feedback

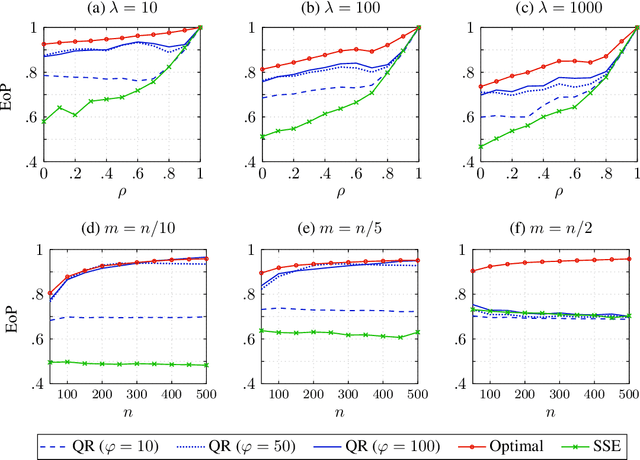
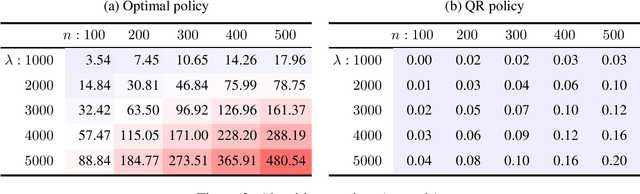
We study Reinforcement Learning from Human Feedback (RLHF), where multiple individuals with diverse preferences provide feedback strategically to sway the final policy in their favor. We show that existing RLHF methods are not strategyproof, which can result in learning a substantially misaligned policy even when only one out of $k$ individuals reports their preferences strategically. In turn, we also find that any strategyproof RLHF algorithm must perform $k$-times worse than the optimal policy, highlighting an inherent trade-off between incentive alignment and policy alignment. We then propose a pessimistic median algorithm that, under appropriate coverage assumptions, is approximately strategyproof and converges to the optimal policy as the number of individuals and samples increases.

Bayesian Persuasion with Externalities: Exploiting Agent Types

We study a Bayesian persuasion problem with externalities. In this model, a principal sends signals to inform multiple agents about the state of the world. Simultaneously, due to the existence of externalities in the agents' utilities, the principal also acts as a correlation device to correlate the agents' actions. We consider the setting where the agents are categorized into a small number of types. Agents of the same type share identical utility functions and are treated equitably in the utility functions of both other agents and the principal. We study the problem of computing optimal signaling strategies for the principal, under three different types of signaling channels: public, private, and semi-private. Our results include revelation-principle-style characterizations of optimal signaling strategies, linear programming formulations, and analysis of in/tractability of the optimization problems. It is demonstrated that when the maximum number of deviating agents is bounded by a constant, our LP-based formulations compute optimal signaling strategies in polynomial time. Otherwise, the problems are NP-hard.

Markov Decision Processes with Time-Varying Geometric Discounting

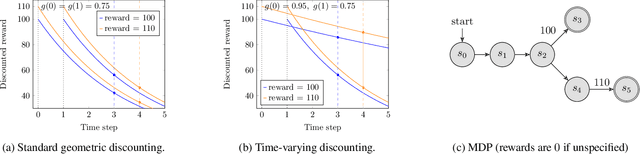
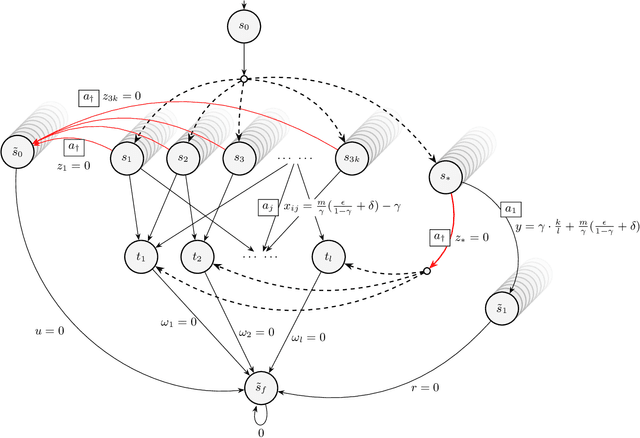
Canonical models of Markov decision processes (MDPs) usually consider geometric discounting based on a constant discount factor. While this standard modeling approach has led to many elegant results, some recent studies indicate the necessity of modeling time-varying discounting in certain applications. This paper studies a model of infinite-horizon MDPs with time-varying discount factors. We take a game-theoretic perspective -- whereby each time step is treated as an independent decision maker with their own (fixed) discount factor -- and we study the subgame perfect equilibrium (SPE) of the resulting game as well as the related algorithmic problems. We present a constructive proof of the existence of an SPE and demonstrate the EXPTIME-hardness of computing an SPE. We also turn to the approximate notion of $\epsilon$-SPE and show that an $\epsilon$-SPE exists under milder assumptions. An algorithm is presented to compute an $\epsilon$-SPE, of which an upper bound of the time complexity, as a function of the convergence property of the time-varying discount factor, is provided.

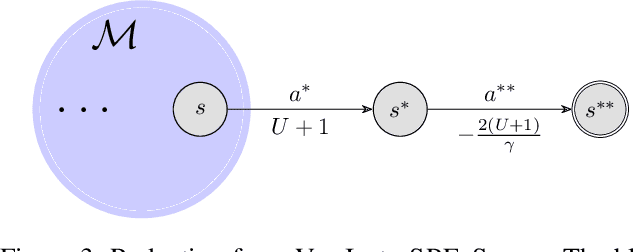
Sequential Principal-Agent Problems with Communication: Efficient Computation and Learning

We study a sequential decision making problem between a principal and an agent with incomplete information on both sides. In this model, the principal and the agent interact in a stochastic environment, and each is privy to observations about the state not available to the other. The principal has the power of commitment, both to elicit information from the agent and to provide signals about her own information. The principal and the agent communicate their signals to each other, and select their actions independently based on this communication. Each player receives a payoff based on the state and their joint actions, and the environment moves to a new state. The interaction continues over a finite time horizon, and both players act to optimize their own total payoffs over the horizon. Our model encompasses as special cases stochastic games of incomplete information and POMDPs, as well as sequential Bayesian persuasion and mechanism design problems. We study both computation of optimal policies and learning in our setting. While the general problems are computationally intractable, we study algorithmic solutions under a conditional independence assumption on the underlying state-observation distributions. We present an polynomial-time algorithm to compute the principal's optimal policy up to an additive approximation. Additionally, we show an efficient learning algorithm in the case where the transition probabilities are not known beforehand. The algorithm guarantees sublinear regret for both players.

Learning to Manipulate a Commitment Optimizer

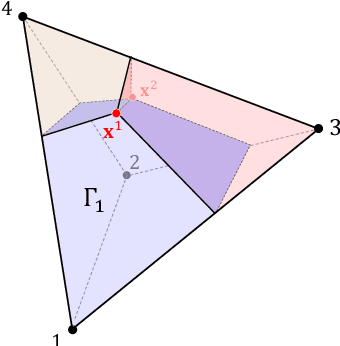
It is shown in recent studies that in a Stackelberg game the follower can manipulate the leader by deviating from their true best-response behavior. Such manipulations are computationally tractable and can be highly beneficial for the follower. Meanwhile, they may result in significant payoff losses for the leader, sometimes completely defeating their first-mover advantage. A warning to commitment optimizers, the risk these findings indicate appears to be alleviated to some extent by a strict information advantage the manipulations rely on. That is, the follower knows the full information about both players' payoffs whereas the leader only knows their own payoffs. In this paper, we study the manipulation problem with this information advantage relaxed. We consider the scenario where the follower is not given any information about the leader's payoffs to begin with but has to learn to manipulate by interacting with the leader. The follower can gather necessary information by querying the leader's optimal commitments against contrived best-response behaviors. Our results indicate that the information advantage is not entirely indispensable to the follower's manipulations: the follower can learn the optimal way to manipulate in polynomial time with polynomially many queries of the leader's optimal commitment.

Online Reinforcement Learning with Uncertain Episode Lengths

Existing episodic reinforcement algorithms assume that the length of an episode is fixed across time and known a priori. In this paper, we consider a general framework of episodic reinforcement learning when the length of each episode is drawn from a distribution. We first establish that this problem is equivalent to online reinforcement learning with general discounting where the learner is trying to optimize the expected discounted sum of rewards over an infinite horizon, but where the discounting function is not necessarily geometric. We show that minimizing regret with this new general discounting is equivalent to minimizing regret with uncertain episode lengths. We then design a reinforcement learning algorithm that minimizes regret with general discounting but acts for the setting with uncertain episode lengths. We instantiate our general bound for different types of discounting, including geometric and polynomial discounting. We also show that we can obtain similar regret bounds even when the uncertainty over the episode lengths is unknown, by estimating the unknown distribution over time. Finally, we compare our learning algorithms with existing value-iteration based episodic RL algorithms in a grid-world environment.

Socially Fair Reinforcement Learning

We consider the problem of episodic reinforcement learning where there are multiple stakeholders with different reward functions. Our goal is to output a policy that is socially fair with respect to different reward functions. Prior works have proposed different objectives that a fair policy must optimize including minimum welfare, and generalized Gini welfare. We first take an axiomatic view of the problem, and propose four axioms that any such fair objective must satisfy. We show that the Nash social welfare is the unique objective that uniquely satisfies all four objectives, whereas prior objectives fail to satisfy all four axioms. We then consider the learning version of the problem where the underlying model i.e. Markov decision process is unknown. We consider the problem of minimizing regret with respect to the fair policies maximizing three different fair objectives -- minimum welfare, generalized Gini welfare, and Nash social welfare. Based on optimistic planning, we propose a generic learning algorithm and derive its regret bound with respect to the three different policies. For the objective of Nash social welfare, we also derive a lower bound in regret that grows exponentially with $n$, the number of agents. Finally, we show that for the objective of minimum welfare, one can improve regret by a factor of $O(H)$ for a weaker notion of regret.

Admissible Policy Teaching through Reward Design

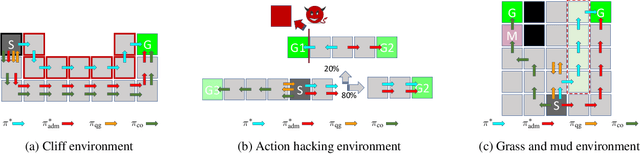
We study reward design strategies for incentivizing a reinforcement learning agent to adopt a policy from a set of admissible policies. The goal of the reward designer is to modify the underlying reward function cost-efficiently while ensuring that any approximately optimal deterministic policy under the new reward function is admissible and performs well under the original reward function. This problem can be viewed as a dual to the problem of optimal reward poisoning attacks: instead of forcing an agent to adopt a specific policy, the reward designer incentivizes an agent to avoid taking actions that are inadmissible in certain states. Perhaps surprisingly, and in contrast to the problem of optimal reward poisoning attacks, we first show that the reward design problem for admissible policy teaching is computationally challenging, and it is NP-hard to find an approximately optimal reward modification. We then proceed by formulating a surrogate problem whose optimal solution approximates the optimal solution to the reward design problem in our setting, but is more amenable to optimization techniques and analysis. For this surrogate problem, we present characterization results that provide bounds on the value of the optimal solution. Finally, we design a local search algorithm to solve the surrogate problem and showcase its utility using simulation-based experiments.

Optimally Deceiving a Learning Leader in Stackelberg Games

Recent results in the ML community have revealed that learning algorithms used to compute the optimal strategy for the leader to commit to in a Stackelberg game, are susceptible to manipulation by the follower. Such a learning algorithm operates by querying the best responses or the payoffs of the follower, who consequently can deceive the algorithm by responding as if his payoffs were much different than what they actually are. For this strategic behavior to be successful, the main challenge faced by the follower is to pinpoint the payoffs that would make the learning algorithm compute a commitment so that best responding to it maximizes the follower's utility, according to his true payoffs. While this problem has been considered before, the related literature only focused on the simplified scenario in which the payoff space is finite, thus leaving the general version of the problem unanswered. In this paper, we fill in this gap, by showing that it is always possible for the follower to compute (near-)optimal payoffs for various scenarios about the learning interaction between leader and follower.

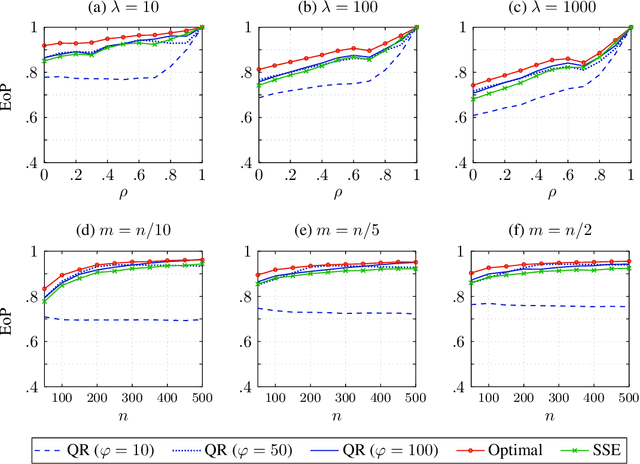
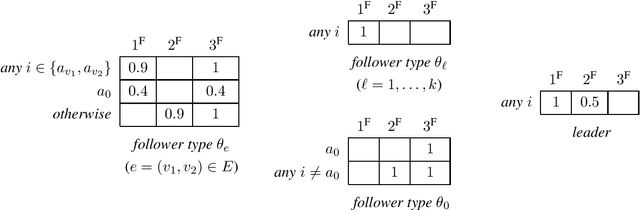
Manipulating a Learning Defender and Ways to Counteract

In Stackelberg security games, information about the attacker's type (i.e., payoff parameters) are essential for computing the optimal strategy for the defender to commit to. While such information can be incomplete or uncertain in practice, algorithms have been proposed to learn the optimal defender commitment from the attacker's best responses during the defender's interaction with the follower. In this paper, we show that, however, such algorithms might be easily manipulated by a strategic attacker, who intentionally sends fake best responses to mislead the learning algorithm into producing a strategy that benefits the attacker but, very likely, hurts the defender. As a key finding in this paper, attacker manipulation normally leads to the defender playing only her maximin strategy, which effectively renders the learning algorithm useless as to compute the maximin strategy requires no information about the other player at all. To address this issue, we propose a game-theoretic framework at a higher level, in which the defender commits to a policy that allows her to specify a particular strategy to play conditioned on the learned attacker type. We then provide a polynomial-time algorithm to compute the optimal defender policy, and in addition, a heuristic approach that applies even when the attacker type space is infinite or completely unknown. It is shown through simulations that our approaches can improve in the defender's utility significantly as compared to the situation when attacker manipulations are ignored.