Manipulating a Learning Defender and Ways to Counteract

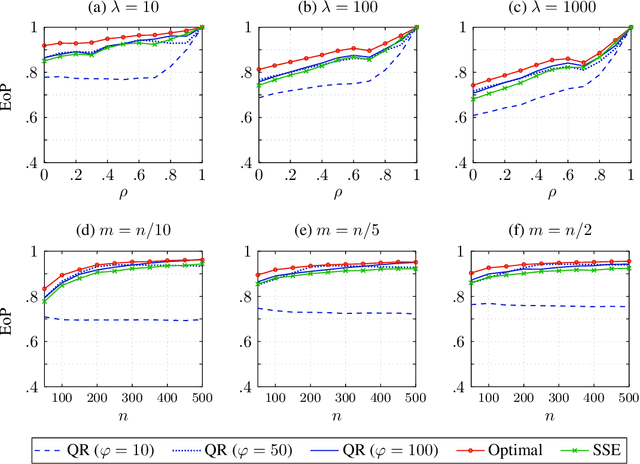
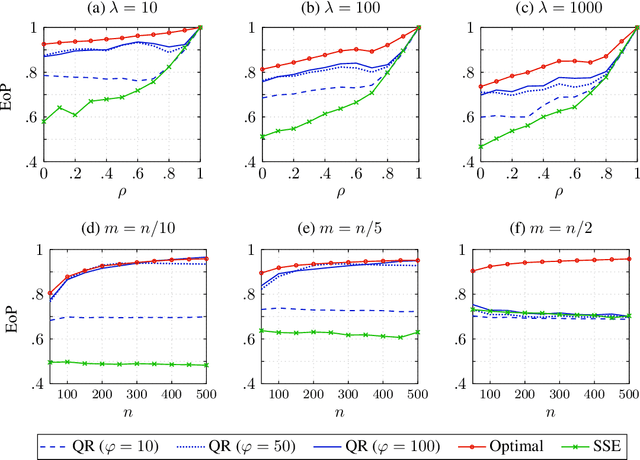
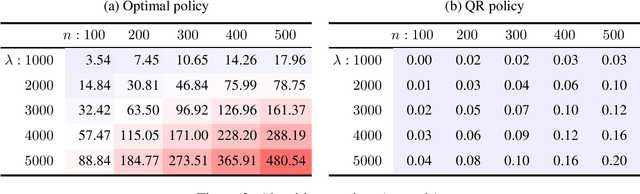
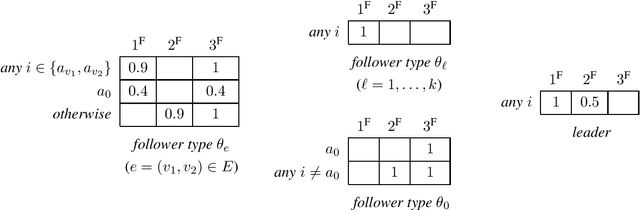
In Stackelberg security games, information about the attacker's type (i.e., payoff parameters) are essential for computing the optimal strategy for the defender to commit to. While such information can be incomplete or uncertain in practice, algorithms have been proposed to learn the optimal defender commitment from the attacker's best responses during the defender's interaction with the follower. In this paper, we show that, however, such algorithms might be easily manipulated by a strategic attacker, who intentionally sends fake best responses to mislead the learning algorithm into producing a strategy that benefits the attacker but, very likely, hurts the defender. As a key finding in this paper, attacker manipulation normally leads to the defender playing only her maximin strategy, which effectively renders the learning algorithm useless as to compute the maximin strategy requires no information about the other player at all. To address this issue, we propose a game-theoretic framework at a higher level, in which the defender commits to a policy that allows her to specify a particular strategy to play conditioned on the learned attacker type. We then provide a polynomial-time algorithm to compute the optimal defender policy, and in addition, a heuristic approach that applies even when the attacker type space is infinite or completely unknown. It is shown through simulations that our approaches can improve in the defender's utility significantly as compared to the situation when attacker manipulations are ignored.