Thomas Kleine Buening
Strategyproof Reinforcement Learning from Human Feedback
Mar 12, 2025Abstract:We study Reinforcement Learning from Human Feedback (RLHF), where multiple individuals with diverse preferences provide feedback strategically to sway the final policy in their favor. We show that existing RLHF methods are not strategyproof, which can result in learning a substantially misaligned policy even when only one out of $k$ individuals reports their preferences strategically. In turn, we also find that any strategyproof RLHF algorithm must perform $k$-times worse than the optimal policy, highlighting an inherent trade-off between incentive alignment and policy alignment. We then propose a pessimistic median algorithm that, under appropriate coverage assumptions, is approximately strategyproof and converges to the optimal policy as the number of individuals and samples increases.
A Unifying Framework for Causal Imitation Learning with Hidden Confounders
Feb 11, 2025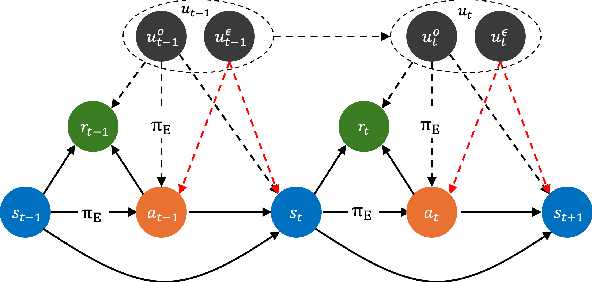

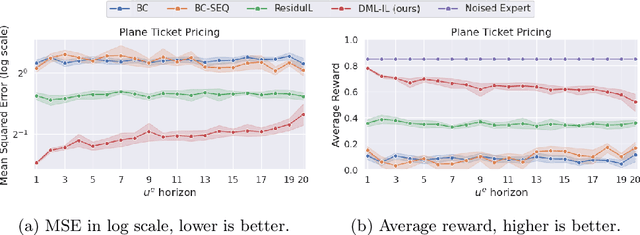
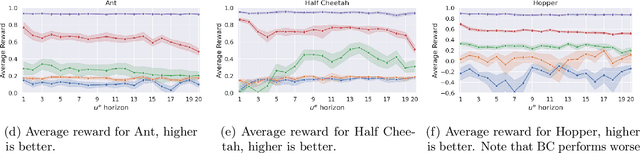
Abstract:We propose a general and unifying framework for causal Imitation Learning (IL) with hidden confounders that subsumes several existing confounded IL settings from the literature. Our framework accounts for two types of hidden confounders: (a) those observed by the expert, which thus influence the expert's policy, and (b) confounding noise hidden to both the expert and the IL algorithm. For additional flexibility, we also introduce a confounding noise horizon and time-varying expert-observable hidden variables. We show that causal IL in our framework can be reduced to a set of Conditional Moment Restrictions (CMRs) by leveraging trajectory histories as instruments to learn a history-dependent policy. We propose DML-IL, a novel algorithm that uses instrumental variable regression to solve these CMRs and learn a policy. We provide a bound on the imitation gap for DML-IL, which recovers prior results as special cases. Empirical evaluation on a toy environment with continues state-action spaces and multiple Mujoco tasks demonstrate that DML-IL outperforms state-of-the-art causal IL algorithms.
A Minimax Approach to Ad Hoc Teamwork
Feb 04, 2025Abstract:We propose a minimax-Bayes approach to Ad Hoc Teamwork (AHT) that optimizes policies against an adversarial prior over partners, explicitly accounting for uncertainty about partners at time of deployment. Unlike existing methods that assume a specific distribution over partners, our approach improves worst-case performance guarantees. Extensive experiments, including evaluations on coordinated cooking tasks from the Melting Pot suite, show our method's superior robustness compared to self-play, fictitious play, and best response learning. Our work highlights the importance of selecting an appropriate training distribution over teammates to achieve robustness in AHT.
Strategic Linear Contextual Bandits
Jun 01, 2024Abstract:Motivated by the phenomenon of strategic agents gaming a recommender system to maximize the number of times they are recommended to users, we study a strategic variant of the linear contextual bandit problem, where the arms can strategically misreport their privately observed contexts to the learner. We treat the algorithm design problem as one of mechanism design under uncertainty and propose the Optimistic Grim Trigger Mechanism (OptGTM) that incentivizes the agents (i.e., arms) to report their contexts truthfully while simultaneously minimizing regret. We also show that failing to account for the strategic nature of the agents results in linear regret. However, a trade-off between mechanism design and regret minimization appears to be unavoidable. More broadly, this work aims to provide insight into the intersection of online learning and mechanism design.
Bandits Meet Mechanism Design to Combat Clickbait in Online Recommendation
Nov 27, 2023
Abstract:We study a strategic variant of the multi-armed bandit problem, which we coin the strategic click-bandit. This model is motivated by applications in online recommendation where the choice of recommended items depends on both the click-through rates and the post-click rewards. Like in classical bandits, rewards follow a fixed unknown distribution. However, we assume that the click-rate of each arm is chosen strategically by the arm (e.g., a host on Airbnb) in order to maximize the number of times it gets clicked. The algorithm designer does not know the post-click rewards nor the arms' actions (i.e., strategically chosen click-rates) in advance, and must learn both values over time. To solve this problem, we design an incentive-aware learning algorithm, UCB-S, which achieves two goals simultaneously: (a) incentivizing desirable arm behavior under uncertainty; (b) minimizing regret by learning unknown parameters. We characterize all approximate Nash equilibria among arms under UCB-S and show a $\tilde{\mathcal{O}} (\sqrt{KT})$ regret bound uniformly in every equilibrium. We also show that incentive-unaware algorithms generally fail to achieve low regret in the strategic click-bandit. Finally, we support our theoretical results by simulations of strategic arm behavior which confirm the effectiveness and robustness of our proposed incentive design.
Minimax-Bayes Reinforcement Learning
Feb 21, 2023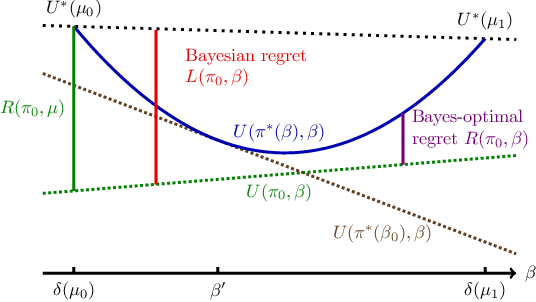

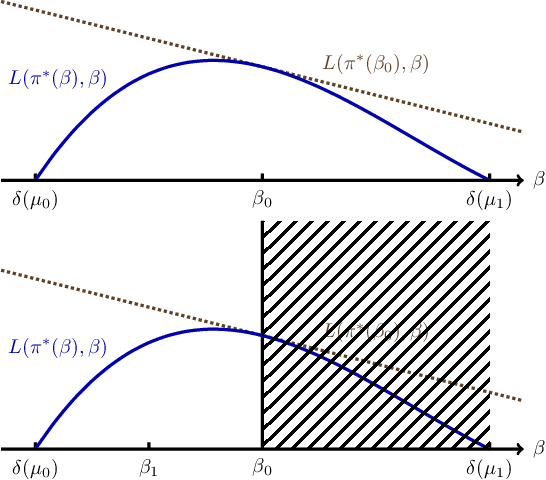
Abstract:While the Bayesian decision-theoretic framework offers an elegant solution to the problem of decision making under uncertainty, one question is how to appropriately select the prior distribution. One idea is to employ a worst-case prior. However, this is not as easy to specify in sequential decision making as in simple statistical estimation problems. This paper studies (sometimes approximate) minimax-Bayes solutions for various reinforcement learning problems to gain insights into the properties of the corresponding priors and policies. We find that while the worst-case prior depends on the setting, the corresponding minimax policies are more robust than those that assume a standard (i.e. uniform) prior.
Environment Design for Inverse Reinforcement Learning
Oct 26, 2022Abstract:The task of learning a reward function from expert demonstrations suffers from high sample complexity as well as inherent limitations to what can be learned from demonstrations in a given environment. As the samples used for reward learning require human input, which is generally expensive, much effort has been dedicated towards designing more sample-efficient algorithms. Moreover, even with abundant data, current methods can still fail to learn insightful reward functions that are robust to minor changes in the environment dynamics. We approach these challenges differently than prior work by improving the sample-efficiency as well as the robustness of learned rewards through adaptively designing a sequence of demonstration environments for the expert to act in. We formalise a framework for this environment design process in which learner and expert repeatedly interact, and construct algorithms that actively seek information about the rewards by carefully curating environments for the human to demonstrate the task in.
ANACONDA: An Improved Dynamic Regret Algorithm for Adaptive Non-Stationary Dueling Bandits
Oct 25, 2022
Abstract:We study the problem of non-stationary dueling bandits and provide the first adaptive dynamic regret algorithm for this problem. The only two existing attempts in this line of work fall short across multiple dimensions, including pessimistic measures of non-stationary complexity and non-adaptive parameter tuning that requires knowledge of the number of preference changes. We develop an elimination-based rescheduling algorithm to overcome these shortcomings and show a near-optimal $\tilde{O}(\sqrt{S^{\texttt{CW}} T})$ dynamic regret bound, where $S^{\texttt{CW}}$ is the number of times the Condorcet winner changes in $T$ rounds. This yields the first near-optimal dynamic regret algorithm for unknown $S^{\texttt{CW}}$. We further study other related notions of non-stationarity for which we also prove near-optimal dynamic regret guarantees under additional assumptions on the underlying preference model.
Interactive Inverse Reinforcement Learning for Cooperative Games
Nov 08, 2021

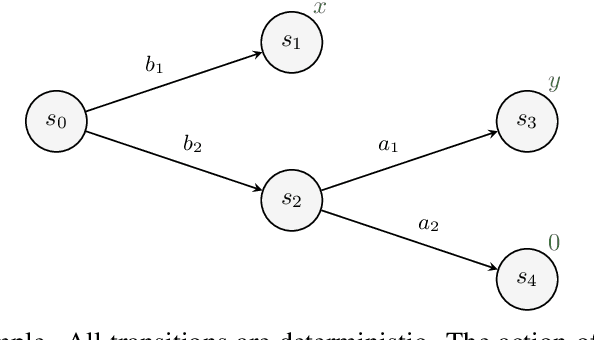
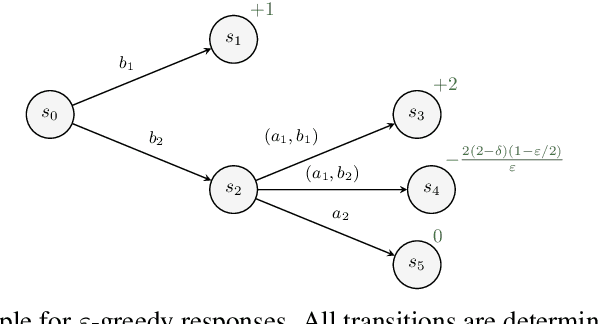
Abstract:We study the problem of designing AI agents that can learn to cooperate effectively with a potentially suboptimal partner while having no access to the joint reward function. This problem is modeled as a cooperative episodic two-agent Markov decision process. We assume control over only the first of the two agents in a Stackelberg formulation of the game, where the second agent is acting so as to maximise expected utility given the first agent's policy. How should the first agent act in order to learn the joint reward function as quickly as possible, and so that the joint policy is as close to optimal as possible? In this paper, we analyse how knowledge about the reward function can be gained in this interactive two-agent scenario. We show that when the learning agent's policies have a significant effect on the transition function, the reward function can be learned efficiently.
Fair Set Selection: Meritocracy and Social Welfare
Feb 23, 2021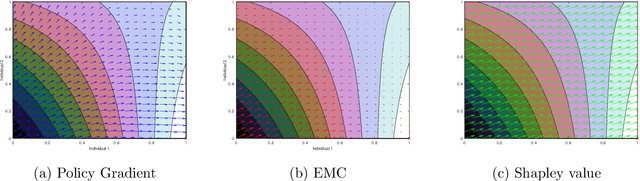
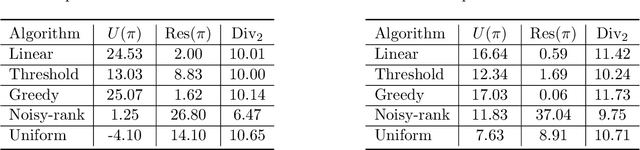
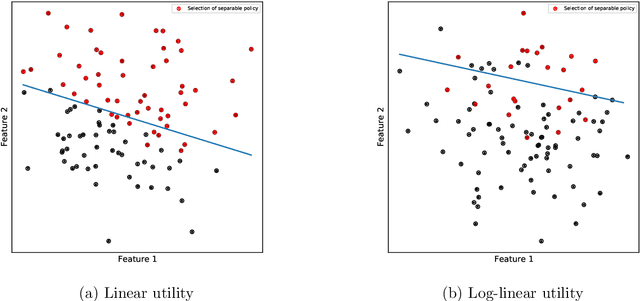
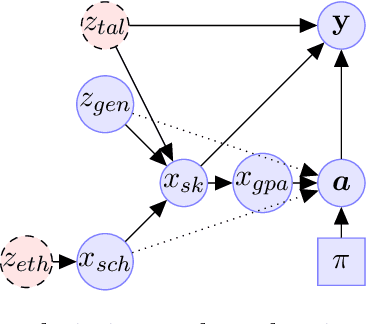
Abstract:In this paper, we formulate the problem of selecting a set of individuals from a candidate population as a utility maximisation problem. From the decision maker's perspective, it is equivalent to finding a selection policy that maximises expected utility. Our framework leads to the notion of expected marginal contribution (EMC) of an individual with respect to a selection policy as a measure of deviation from meritocracy. In order to solve the maximisation problem, we propose to use a policy gradient algorithm. For certain policy structures, the policy gradients are proportional to EMCs of individuals. Consequently, the policy gradient algorithm leads to a locally optimal solution that has zero EMC, and satisfies meritocracy. For uniform policies, EMC reduces to the Shapley value. EMC also generalises the fair selection properties of Shapley value for general selection policies. We experimentally analyse the effect of different policy structures in a simulated college admission setting and compare with ranking and greedy algorithms. Our results verify that separable linear policies achieve high utility while minimising EMCs. We also show that we can design utility functions that successfully promote notions of group fairness, such as diversity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge